转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1300587979
设原序列S的逆序列为S' ,则这道题目的关键在于,
最少需要补充的字母数 = 原序列S的长度 — S和S'的最长公共子串长度
这个公式我不证明,不难证
剩下的就小意思了,最基础的LCS题。
注意本题空间开销非常大,需要适当的处理手法
先看看几种不同的申请空间方法的区别:
1. 静态数组 开销大小为5001*5001的int是铁定超的.
据说用short int的话不会MLE,有兴趣的同学可以试试
2. 动态数组 单纯的申请动态数组是不能解决这个问题的,动态数组只能增加空间利用率,
但是本题最恶劣的数组大小还是5001*5001,动态数组是不能改变这个事实的
3. 滚动数组 这里重点讲一下滚动数组在这个题目中的应用.自己目前理解的应用滚动数组的目的就是减少空间开销.首先可以在纸上简单模拟一下DP的转移过程.确定好最少行数或者列数之后,重点就是在如何进行"滚动"以及如何用表达式控制这个滚动.
对于本题,我用的是行数以0--1--0—1的滚动方式,滚动表达式为i%2和(i-1)%2 ,没错,就是强大的求余滚动O(∩_∩)O
由于应用了滚动数组,那么空间开销就能够从5001*5001压缩到 2*5001 !!!
哈哈,傻眼了吧\(^o^)/~
而且本题我为了稍微提高一点空间利用率,使用了 动态二维滚动数组,就是东邪(动态)西毒(滚动)的混合体O(∩_∩)O,这样做的目的,只是对测试数据库的数据抱有一点点希望:我相信它们不全都是5000的长度,所以我想能尽可能再节省一点列数….不过时间就惨不忍睹咯,1157ms….不过空间开销却由MLE跌落到谷底的280K\(^o^)/~
跪求传说中 300K 16ms代码………….
顺便贴一下LCS的图解算法
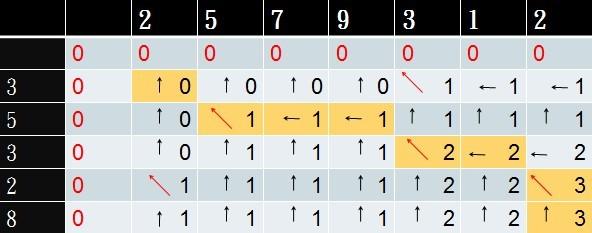
s1:2 5 7 9 3 1 2
s2:3 5 3 2 8
一. 使用二維陣列
二. 記錄每一格的結果,是由哪一格而來
1. 陣列開頭均設為空
2. S1[i]=S2[j]相同,dp[i][j]则继承左上方向dp[i-1][j-1]的值+1
3. 不相同dp[i][j]则继承 上方與左方中的最大數值
最后整个二維陣列中最大的值,就是s1和s2的最长公共子串长度
1 //Memory Time
2 //280K 1157MS
3
4 #include<iostream>
5 using namespace std;
6
7 int max(int a,int b)
8 {
9 return a>b?a:b;
10 }
11
12 int main(int i,int j)
13 {
14 int n;
15 while(cin>>n)
16 {
17 /*Input*/
18
19 char* s1=new char[n+1];
20 char* s2=new char[n+1]; //s1的逆序列
21
22 int **dp=new int*[n+1]; //定义二维动态滚动数组(本题以01行滚动)
23 dp[0]=new int[n+1];
24 dp[1]=new int[n+1];
25 dp[0][0]=dp[1][0]=0; //动态数组初始化 行开头为全0
26
27 for(i=1,j=n;i<=n;i++,j--)
28 {
29 dp[0][i]=dp[1][i]=0; //动态数组初始化 列开头为全0
30
31 char temp;
32 cin>>temp;
33 s1[i]=s2[j]=temp;
34 }
35
36 /*Dp-LCS*/
37
38 int max_len=0;
39 for(i=1;i<=n;i++)
40 for(j=1;j<=n;j++)
41 {
42 if(s1[i]==s2[j])
43 dp[i%2][j]=dp[(i-1)%2][j-1]+1; //如果字符相等,则继承前一行前一列的dp值+1
44 else
45 dp[i%2][j]=max(dp[(i-1)%2][j],dp[i%2][j-1]); //否则,取上方或左方的最大dp值
46
47 if(max_len<dp[i%2][j])
48 max_len=dp[i%2][j];
49 }
50
51 cout<<n-max_len<<endl;
52
53 delete s1;
54 delete s2;
55 delete[] dp;
56 }
57 return 0;
58 }