队列课下作业——杨辉三角

队列课下作业——杨辉三角

作业要求

1 用实现循环队列

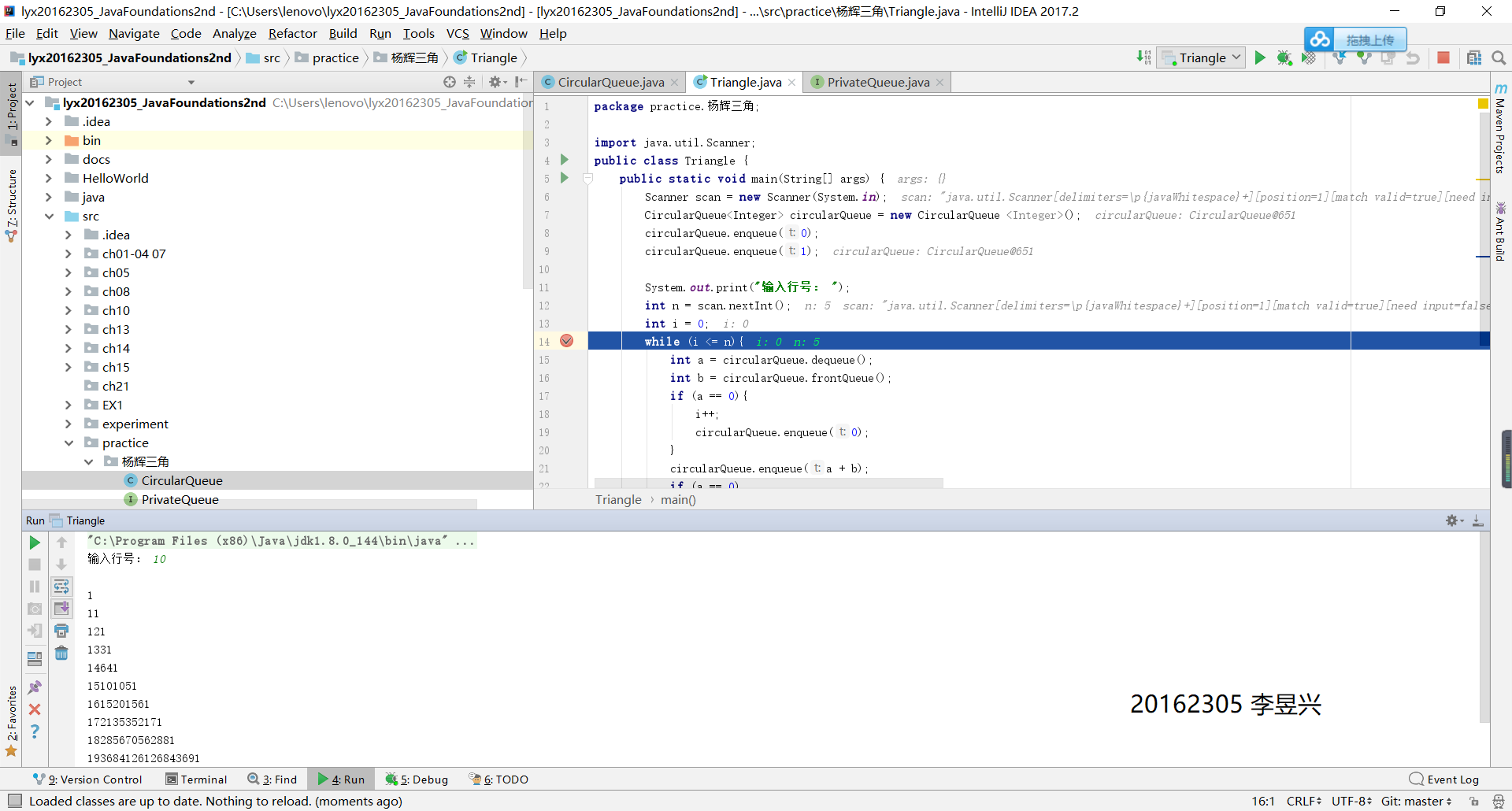
2 参考PPT用循环队列打印杨辉三角

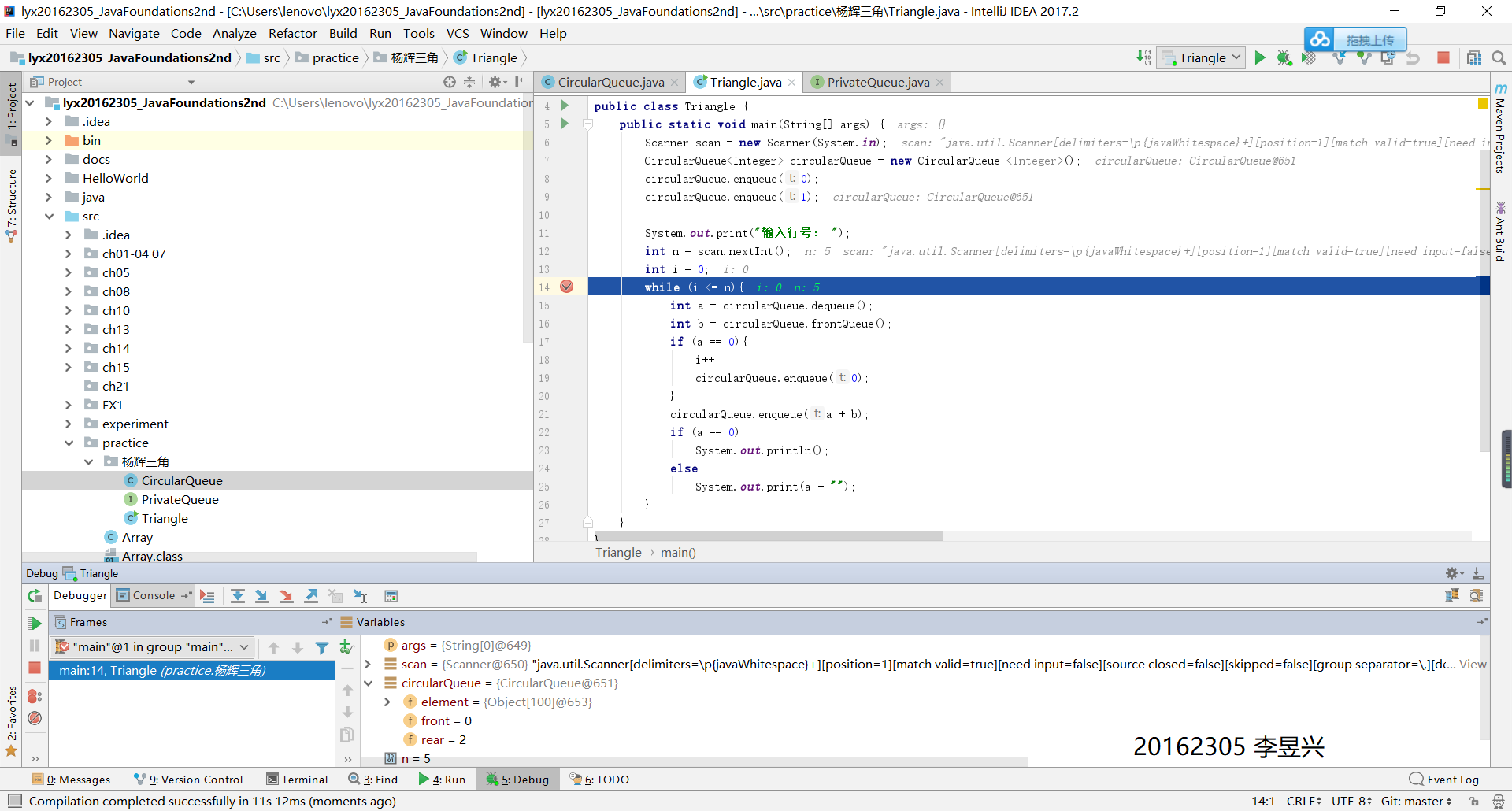
3 用JDB或IDEA单步跟踪排队情况，画出队列变化图，包含自己的学号信息

4 把代码推送到代码托管平台

5 把完成过程写一篇博客：重点是单步跟踪过程和遇到的问题及解决过程

6 提交博客链接

设计思路和实验代码

• 1、接口

interface PrivateQueue<T> {
    public boolean isEmpty();
    public T dequeue();

}

• 2、循环队列类
• isEmpty方法
• 判断循环队列是否为空，如果循环队列的front和rear相等，则说明两者重合，队列为空，返回true，不空的话返回false。

    public boolean isEmpty() {
        if (front == rear) 
            return true;
        else 
            return false;
    }

• dequeue方法
• 这个方法是出队操作，让队列第一个元素从队列中出去。如果队列为空则直接返回null，不为空的话，将第一个元素赋值给t，再将（front + 1）和队列长度做取余处理，得到的值赋给新的front，返回t，完成第一个元素出队列操作。

public T dequeue() {
        if (isEmpty())
            return null;

        T t = (T) queue[front];
        front = (front + 1) % queue.length;
        return t;
    }

• enqueue方法
• 这个方法我是引用的教材上的代码，如果count和队列长度相等，则扩大队列长度为原来的二倍。添加进队列的方法，是将t赋值给原来rear指向的最后一个元素，然后rear加一和队列的长度取余，将这个值赋给新的rear。入队操作填充的是数组最后一个单元的时候，rear的值必须置为0，表示下一个元素应该保存在下标为0处。

  public void enqueue(T t) {
        if (count == queue.length)
            expandCapacity();
        queue[rear] = t;
        rear = (rear + 1) % queue.length;
        count++;
    }
    

• expandCapacity方法
• 这个方法是扩大队列的长度为原来的二倍。为了能够添加元素，而队列又已经充满，则需要对原来的队列扩大规模。先定义一个原来队列长度二倍的新的队列larger，再利用for循环，将原来队列中的值一一对应到新的数组中，front为0，rear和队列规模count相等，最后将新的二倍长队列赋给queue。

public void expandCapacity(){
        T[] larger = (T[])(new Object[queue.length*2]);

        for (int index = 0; index<count; index++)
            larger[index] = (T) queue[(front + index) % queue.length];
        front = 0;
        rear = count;
        queue = larger;
    }
    

• frontQueue方法
• 这个方法获取队列中的第一个元素，如果为空，返回null，不为空的话，获取第一个元素赋值给t并返回t。

    public T frontQueue() {
        if (isEmpty()) return null;

        T t = (T) this.queue[this.front];
        return t;
    }
    

单步跟踪和杨辉三角实现截图