codeforces 437D The Child and Zoo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Of course our child likes walking in a zoo. The zoo has n areas, that are numbered from 1 to n. The i-th area contains a_i animals in it. Also there are m roads in the zoo, and each road connects two distinct areas. Naturally the zoo is connected, so you can reach any area of the zoo from any other area using the roads.

Our child is very smart. Imagine the child want to go from area p to area q. Firstly he considers all the simple routes from p to q. For each route the child writes down the number, that is equal to the minimum number of animals among the route areas. Let's denote the largest of the written numbers as f(p, q). Finally, the child chooses one of the routes for which he writes down the value f(p, q).

After the child has visited the zoo, he thinks about the question: what is the average value of f(p, q) for all pairs p, q (p ≠ q)?

Can you answer his question?

Input

The first line contains two integers n and m (2 ≤ n ≤ 10⁵; 0 ≤ m ≤ 10⁵). The second line contains n integers: a₁, a₂, ..., a_n (0 ≤ a_i ≤ 10⁵). Then follow m lines, each line contains two integers x_i and y_i (1 ≤ x_i, y_i ≤ n; x_i ≠ y_i), denoting the road between areas x_i and y_i.

All roads are bidirectional, each pair of areas is connected by at most one road.

Output

Output a real number — the value of .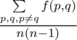

The answer will be considered correct if its relative or absolute error doesn't exceed 10^- 4.

Sample test(s)

input

4 3
10 20 30 40
1 3
2 3
4 3

output

16.666667

input

3 3
10 20 30
1 2
2 3
3 1

output

13.333333

input

7 8
40 20 10 30 20 50 40
1 2
2 3
3 4
4 5
5 6
6 7
1 4
5 7

output

18.571429

Note

Consider the first sample. There are 12 possible situations:

• p = 1, q = 3, f(p, q) = 10.
• p = 2, q = 3, f(p, q) = 20.
• p = 4, q = 3, f(p, q) = 30.
• p = 1, q = 2, f(p, q) = 10.
• p = 2, q = 4, f(p, q) = 20.
• p = 4, q = 1, f(p, q) = 10.

Another 6 cases are symmetrical to the above. The average is .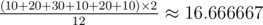

Consider the second sample. There are 6 possible situations:

• p = 1, q = 2, f(p, q) = 10.
• p = 2, q = 3, f(p, q) = 20.
• p = 1, q = 3, f(p, q) = 10.

Another 3 cases are symmetrical to the above. The average is .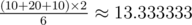

译文

当然了，我们的小朋友是非常喜欢在动物园游玩的。这个动物园有n个区域，编号为1至n，第i个区域有a[i]仅仅动物。动物园里还有m条路，每条路连接两个不同样的区域。动物园自然是连通的——你能够从不论什么一个区域到达随意的其它区域。
我们的小朋友非常聪明。如果他打算从区域p走到区域q。他首先会考虑全部从p走到q的简单路径，然后对于每一条路径，他都会写下路径上的区域中动物数量的最小值。

我们记这些写下的数字中最大的为f(p,q)。终于，他会选择一条值为f(p,q)的路径。
在他游玩这个公园之后。他想到了这样一个问题：全部f(p,q)(p不等于q)的平均值是多少？你能回答这个问题吗？
Input
第一行是n,m(2<=n<=10^5; 0<=m<=10^5)。第二行有a[1],a[2],...,a[n](0<=a[i]<=10^5)。接下来m行，每行有两个整数x[i]和y[i]（1<=x[i],y[i]<=n; x[i]不等于y[i]），表示一条连接x[i]和y[i]的道路。
全部道路都是双向。每对区域至多由一条道路直接连接。
Output
输出一个实数——全部f(p,q)之和(p不等于q)除以n(n-1)的值。

假设你的答案与标准答案的相对误差或绝对误差不超过10^(-4)，就会被觉得是正确的。

题解

带权并查集、最大生成树。

想清楚了非常easy。

首先设从x点到y点，要进过k条路：1、每条路连接的两个点中，点权值小的点对答案有贡献，我们能够把这条边的边权记为“这条路连接的两个点中点较小的权值”。2、全部k条路中，边权最大的为f（x，y）。

以上因为要找最大（贪心，且在图中），就想到了最大生成树。

接下来是计数问题。

记一下每一个集合中的元素就可以。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int n,m,fa[100002];
ll a[100002],size[100002],ans;
struct bian {int x,y;ll v;} e[100002];
void init()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	   {scanf("%I64d",&a[i]);
	    fa[i]=i; size[i]=1;
	   }
	for(int i=1;i<=m;i++)
	   {scanf("%d%d",&e[i].x,&e[i].y);
	    e[i].v=min(a[e[i].x],a[e[i].y]);
	   }
}
bool kp(const bian &u,const bian &w)
{return u.v>w.v;}
int find(int x)
{
	if(fa[x]!=x) fa[x]=find(fa[x]);
	return fa[x];
}
void klskl()
{
	sort(e+1,e+m+1,kp);
	for(int i=1;i<=m;i++)
	   {int r1=find(e[i].x),r2=find(e[i].y);
	    if(r1!=r2)
	       {ans+=e[i].v*size[r1]*size[r2];
	        size[r1]+=size[r2];
	        fa[r2]=r1;
		   }
	   }
	ll chus=(ll)n*(n-1)/2;//注意：一定要有这句话否则会wa。 
	double ans2=(double)ans/chus;
	printf("%.6lf",ans2);
}
int main()
{
	init(); klskl(); return 0;
}