概述
$AC$自动机是以$Trie$为结构基础,$kmp$为思想基础建立的,主要用于多模式串匹配。
在$AC$自动机上,所有的模式串构成一棵$Trie$树,而且利用$kmp$的思想,在$Trie$上构造失配指针。
$Trie$上的结点表示的是某个模式串的前缀,相当于一种状态,而$Trie$上的边就相当于是状态的转移。
$fail$指针
先把所有的模式串放到$Trie$,举例如下:

假如说现在要匹配的文本串是$ABCD$,我们去树上匹配,会经过$2,3,4$号节点匹配到模式串$ABC$,然后就不能继续匹配。
如果接下来重新从根结点开始,复杂度会很高,我们可以借用$kmp$的思想,跳到$7$去,$7$就是$4$的失配指针。
More officially,$fail$指针指向 / 模式串的前缀中 / 匹配 / 当前状态的最长后缀。(断句要断好)
也就是说,$i$的失配指针$j$,满足$root->j$是$root->i$的一个后缀,而且是所有满足$root->i=root->j_x$中最大的那一个$j_x$。
$9$号点也满足条件,但是那里不是最长后缀,所以我们不跳到那里去。
下面是$fail$的求法:
设$Trie$上当前的节点是$u$,$u$的父亲是$p$,$trie[p][c]=u$。
假设深度小于$u$的所有结点的$fail$指针都已经求过。
1.$trie[fail[p]][c]$存在,那么$fail[u]=trie[fail[p]][c]$。$p$的最长后缀的位置在$fail[p]$,在$fail[p]$的位置再加一个字符$c$就一定$u$的最长后缀的位置,因为只在一个确定的串后面加上一个字符而已。
2.如果$trie[fail[p]][c]$不存在,那么就要一直跳$fail$指针(反复横跳),找$trie[fail[fail[p]]][c]$,直到它存在,然后重复1.
3.如果真的不存在,那么把$fail$指向根。
具体可以用$bfs$实现(有假设深度小于$u$的所有结点的$fail$指针都已经求过)
$tr[u][c]$可以理解为字典树上的一条边,也可以理解为一种状态转移,表示$u$加上一个字符$c$达到的状态。
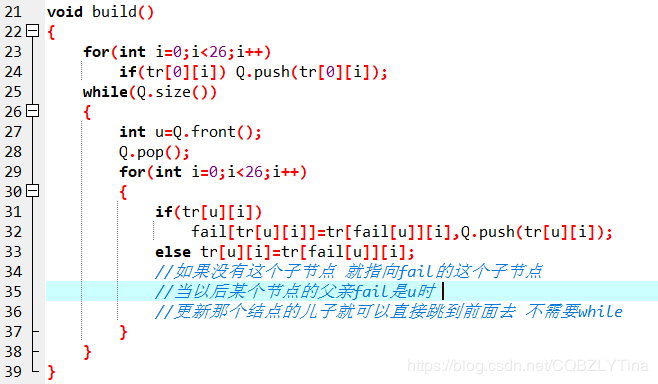
代码实际上修改了$Trie$的结构,但是使得匹配转移更加完善。它将 fail 指针跳转的路径做了压缩(就像并查集的路径压缩),使得本来需要跳很多次$ail$针变成跳一次。
匹配函数
$fail$是最难的部分,$fail$理解之后求答案就水到渠成了吧。
时间复杂度

【参考:OIwiki】