前言
好久之前就讲过,但还是用得不是很熟练(难道是因为我总是写暴力?)。还是复习一下吧,由于是复习,可能会不是很详细,比起原理更侧重于用法什么的。
如果之前没有接触过,还是看这篇博文吧。(是我入门的时候看的博客)
原理
简单说一下吧。
其实树状数组和二进制有着密切的关系。
就像所有的整数都可以表示成2的次方的和那样,我们也可以考虑把一串序列表示成一系列子序列的和,将一个前缀和划分成了多个子序列的和,而划分的方法与数的2的幂和具有及其相似的方式。

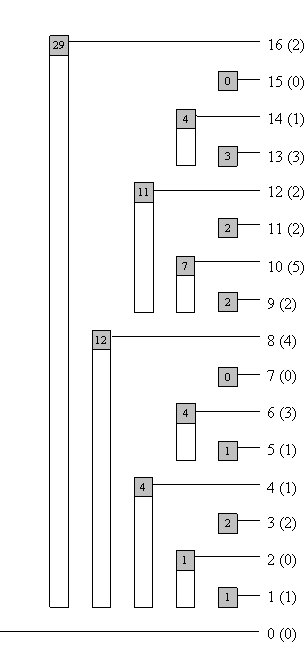
左边是空的树状数组的形态,右边是放了值进去的树状数组。
假设我们要计算$a[1]..a[13]$的和,即$sum[13]$ 由于$13$的二进制表示为$1101$,那么就有:
$sum[1101] = tree[1101] + tree[1100] + tree[1000]$
可以用最简单的位运算实现取出一个整数的二进制形式中的最右一个“1”的位置: i&(-i)
这个数有个专门的称呼,叫$lowbit$
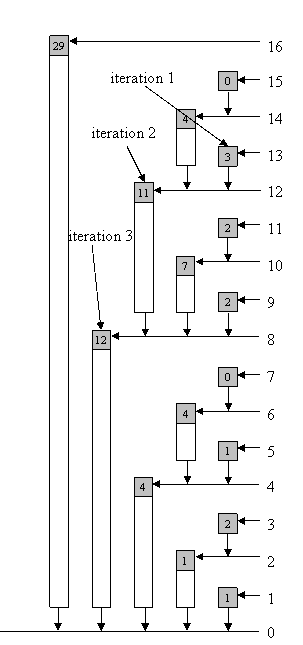
求前缀和的图示
应用-单点修改,区间查询
最基础的类型,就不多说了。

1 #include<cstdio> 2 using namespace std; 3 #define N 500005 4 int n,m; 5 int a[N],tree[N]; 6 int rd() 7 { 8 int f=1,x=0;char c=getchar(); 9 while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();} 10 while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();} 11 return f*x; 12 } 13 int lowbit(int x) 14 { 15 return x&(-x); 16 } 17 int query(int x) 18 { 19 int ans=0; 20 for(;x;x-=lowbit(x)) 21 ans+=tree[x]; 22 return ans; 23 } 24 void update(int x,int val) 25 { 26 for(;x<=N;x+=lowbit(x)) 27 tree[x]+=val; 28 return ; 29 } 30 int main() 31 { 32 n=rd(),m=rd(); 33 for(int i=1;i<=n;i++) 34 { 35 a[i]=rd(); 36 update(i,a[i]); 37 } 38 for(int i=1;i<=m;i++) 39 { 40 int opt=rd(),x=rd(),y=rd(); 41 if(opt==1) update(x,y); 42 if(opt==2) printf("%d ",query(y)-query(x-1)); 43 } 44 return 0; 45 }
应用-区间修改,单点查询
如果对区间中的每一个数都进行修改,时间复杂度显然无法承受。
考虑用差分建树。
举个例子:
原数组$A$为: $1$ $3$ $3$ $5$ $3$ $2$
差分数组$D$为: $1$ $2$ $0$ $2$ $-2$ $-1$
操作是给区间$[2,4]$加上$3$
原数组变为: $1$ $6$ $6$ $8$ $3$ $2$
差分数组变为: $1$ $5$ $0$ $2$ $-5$ $-1$
注意到区间内的差值不会改变,对区间$[l,r]$进行操作时,会对差分数组的$l$位置进行相同的操作,对$r+1$的位置进行相反操作。
利用这个性质,将差分数组建树,就把更新一个区间变成了更新两个点。
最后单点查询的时候$A[i]$就是$D[1~i]$的前缀和。

1 #include<cstdio> 2 using namespace std; 3 #define N 500005 4 int n,m; 5 int a[N],tree[N]; 6 int rd() 7 { 8 int f=1,x=0;char c=getchar(); 9 while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();} 10 while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();} 11 return f*x; 12 } 13 int lowbit(int x) 14 { 15 return x&(-x); 16 } 17 int query(int x) 18 { 19 int ans=0; 20 for(;x;x-=lowbit(x)) 21 ans+=tree[x]; 22 return ans; 23 } 24 void update(int x,int val) 25 { 26 for(;x<=N;x+=lowbit(x)) 27 tree[x]+=val; 28 return ; 29 } 30 int main() 31 { 32 n=rd(),m=rd(); 33 for(int i=1;i<=n;i++) 34 { 35 a[i]=rd(); 36 update(i,a[i]-a[i-1]); 37 } 38 for(int i=1;i<=m;i++) 39 { 40 int opt=rd(); 41 if(opt==1) 42 { 43 int x=rd(),y=rd(),k=rd(); 44 update(x,k); 45 update(y+1,-k); 46 } 47 if(opt==2) 48 { 49 int x=rd(); 50 printf("%d ",query(x)); 51 } 52 } 53 return 0; 54 }
应用-区间修改,区间查询
用差分建树,最后前缀和得到的也还是一个点的值。
那么要区间查询怎么办呢?当然可以用线段树,不过这里要说的是树状数组。
还是利用以上的差分:
$A[i]=D[1]+D[2]+...+D[i]$
则$A[1]+A[2]+...+A[i]=(D[1])+(D[1]+D[2])+...+(D[1]+D[2]+D[3]+...+D[i])=D[1]*i+D[2]*(i-1)+...+D[i]$
为了方便,存储的值不要和$i$扯上关系,所以继续化简成这个样子:
原式$=n*(D[1]+D[2]+...+D[i])-(D[1]*0+D[2]*1+D[3]*2+...+D[i]*(i-1))$
所以就维护两个树状数组,一个的$query1(i)$是$D[1]+D[2]+D[3]+...D[i]$,另一个的$query2(i)$是$D[1]*0+D[2]*1+D[3]*2+...+D[i]*(i-1)$。
最后区间查询的答案就是$(query1(r)*r-query2(r))-(query1(l-1)*r-query2(l-1))$

1 #include<cstdio> 2 using namespace std; 3 #define N 100005 4 #define ll long long 5 int n,m; 6 ll a[N],t1[N],t2[N]; 7 int rd() 8 { 9 int f=1,x=0;char c=getchar(); 10 while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();} 11 while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();} 12 return f*x; 13 } 14 int lowbit(int x) 15 { 16 return x&(-x); 17 } 18 ll query(int x) 19 { 20 ll ans=0; 21 int i=x; 22 for(;x;x-=lowbit(x)) 23 ans+=(t1[x]*i-t2[x]); 24 return ans; 25 } 26 void update(int x,ll val) 27 { 28 int i=x; 29 for(;x<=N;x+=lowbit(x)) 30 t1[x]+=val,t2[x]+=val*(i-1); 31 return ; 32 } 33 int main() 34 { 35 n=rd(),m=rd(); 36 for(int i=1;i<=n;i++) 37 { 38 scanf("%lld",&a[i]); 39 update(i,a[i]-a[i-1]); 40 } 41 for(int i=1;i<=m;i++) 42 { 43 int opt=rd(),x=rd(),y=rd(); 44 if(opt==1) 45 { 46 ll delta;scanf("%lld",&delta); 47 update(x,delta); 48 update(y+1,-delta); 49 } 50 if(opt==2) 51 printf("%lld ",query(y)-query(x-1)); 52 } 53 return 0; 54 }
小结
更多的时候,树状数组不会单独出题,而是作为一种工具。
线段树也可以实现它的功能,不过相较之下,树状数组更为轻巧好写,常数也更小,平时没什么大事(误)的时候就用它啦。
