题目大意:
一个$n*m$的网格图,每个格子可以染黑色、白色,问每个格子最多有一个相邻格子颜色相同的涂色方案数
$n,m<=1e5$
分析:
首先,考虑到如果有两个相邻的格子颜色相同,那么这两行/列的格子状态就确定了。比如:
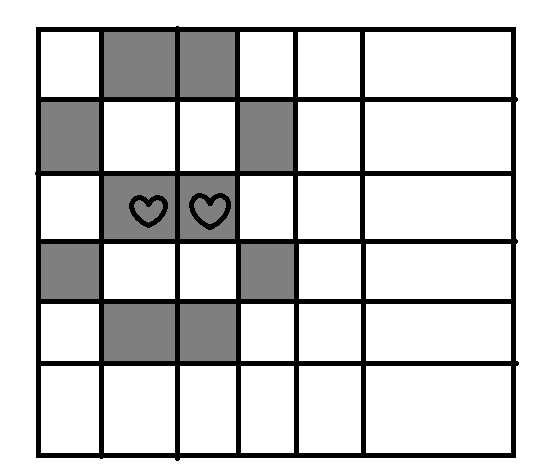
在中间两个爱心格子被确定的情况下,第二列和第三列的涂色情况就已经被确定了。实际上,第一列和第四列涂的颜色也确定了。(最后这句话我们留着待会儿分析)
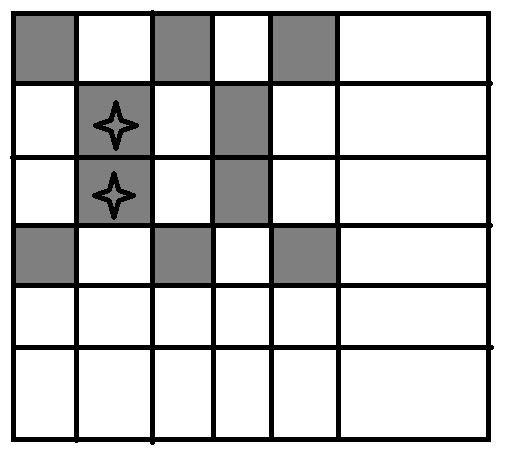
同理,在中间两个星星确定的时候,第二行和第三行的涂色情况也唯一确定。实际上,第一行和第四列涂的颜色也确定了。
假如说在一个方格中,既有横着出现的两个连续的一样颜色的格子,也有竖着出现的两个连续的一样颜色的格子,就像这样:
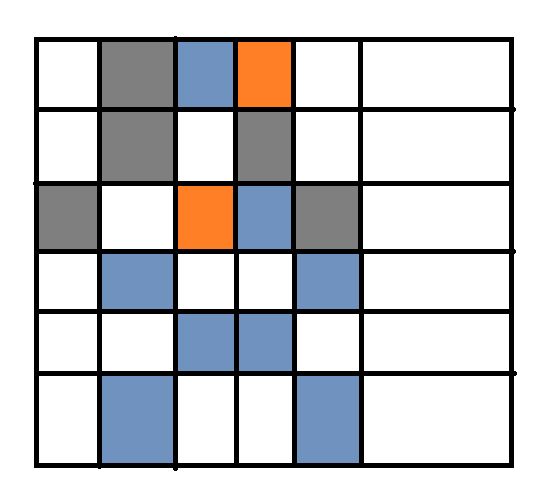
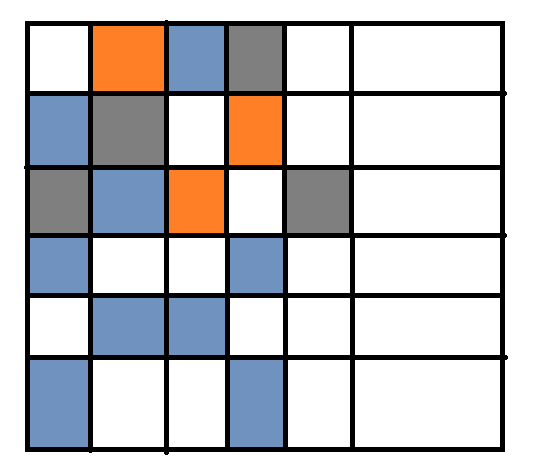

那么一定会产生矛盾,无论怎么挪都会产生矛盾。(橙色的部分是既需要用灰色,也需要用蓝色涂的格子,是矛盾的地方)
所以,在一种着色方案中,这种相邻两个颜色一样的情况只会在一个方向中出现,我们只需要考虑一个方向那么多行的方案数,另外一个方向的同理就好。
如果已经确定相邻两个颜色一样的格子出现的方向(为方便讨论,下面我们假设这两个格子是竖着的),那么每一行的格子颜色一定是交错的,两行之间要么一样,要么颜色相反,而且颜色一样的不能连着出现3次及以上。
在第一行确定的情况下,如果要求每一个格子的每个相邻格子的颜色都和他不一样,那么这是一个棋盘染色,就唯一确定了。
但是,按照这道题的条件来说的话,后面的格子可以有两行,也可以只有一行。(就是一次性确定两行或一次性确定一行)
Like this:
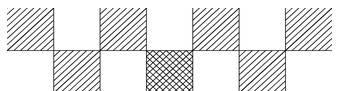
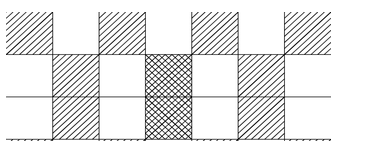
设$f[i]$表示铺到第$i$行(前$i$行)的方案总数,那么递推式就是$f[i]=f[i-1]+f[i-2]$
(初始化$f[0]=1$是一开始就是两行连着一样的情况)
答案就是$f[n]$。
然后,还有相邻两个颜色一样的格子是竖着的,方案数就是$f[m]$,这两类在前面已经说过没有交集,答案就是$f[n]+f[m]$
然后,棋盘染色的情况在两种情况中都被计算了,所以答案要减1。
最后,黑白颜色可以反过来,所以乘2.
做完了,$Nice!$

1 /* 2 ID: Starry21 3 */ 4 #include<iostream> 5 #include<string> 6 #include<cstdio> 7 #include<cstring> 8 #include<map> 9 #include<algorithm> 10 using namespace std; 11 #define N 100005 12 #define ll long long 13 #define MOD 1000000007 14 int n,m; 15 ll f[N]; 16 int main() 17 { 18 scanf("%d %d",&n,&m); 19 f[0]=f[1]=1; 20 for(int i=2;i<=max(n,m);i++) 21 f[i]=(f[i-1]+f[i-2])%MOD; 22 printf("%lld ",2*((f[n]+f[m])%MOD-1+MOD)%MOD); 23 return 0; 24 }
