题意:
给定一个括号序列,随意交换两个位置的括号之后,问有多少个不同长度的圈。关于圈的定义大概就是:将括号序列的后$k$个数放到括号序列的最前面,就是长度为$k$的圈。(看了好久题意emmm...)
分析:
首先,我们可以$n^2$暴力枚举交换的位置,然后再看有多少个圈。
然后,对于括号序列的正确性判断,有一个非常巧妙的方法,(只适用于只有一种括号,既有小括号,又有中括号是不得行的):
给$"("$赋值为1,$")"$赋值为-1,计算这个序列的前缀和,只要保证前缀和的每一位都大于等于0,并且最后一位刚好等于0,这个序列就是正确的括号序列。
然后再枚举一个$k$,也就是圈的长度。要判断这个$k$成不成立,也就是要保证变换之后的前缀和每一个都要大于等于0。
根据数学课上老师的传授,这是一个恒成立问题,我们只需要让最小的那个数在变换之后大于等于0就可以了。
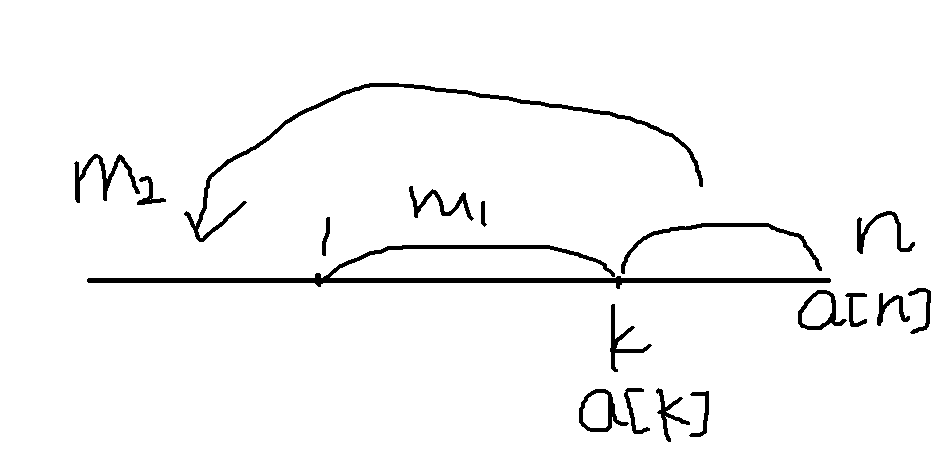
用一个前缀最小值和后缀最小值,$m1[k]$表示$1~k$的最小值,$m2[k]$表示$k~n$的最小值,在变换之后,如果$m1[k]+(a[n]-a[i])>=0$&&$m2[k+1]-a[i]>=0$,那么就符合条件。

1 #include<iostream> 2 #include<string> 3 #include<cstdio> 4 #include<cstring> 5 #include<map> 6 #include<algorithm> 7 using namespace std; 8 #define N 505 9 #define ll long long 10 #define INF 0x3f3f3f3f 11 int n,ans,l,r; 12 char s[N]; 13 int a[N]/*前缀和*/,min1[N]/*前缀最小值*/,min2[N]/*后缀最小值*/; 14 void swp(int i,int j) 15 { 16 char tmp=s[i]; 17 s[i]=s[j],s[j]=tmp; 18 } 19 int f() 20 { 21 int res=0; 22 for(int i=1;i<=n;i++) 23 { 24 if(s[i]=='(') a[i]=a[i-1]+1; 25 if(s[i]==')') a[i]=a[i-1]-1; 26 min1[i]=min2[i]=INF; 27 min1[i]=min(min1[i-1],a[i]); 28 } 29 for(int i=n;i>=1;i--) 30 min2[i]=min(min2[i+1],a[i]); 31 if(min1[n]>=0&&a[n]==0) res++;//不进行轮换就已经是正确的序列 32 for(int i=1;i<n;i++)//从i和i+1之间断开 33 if(min2[i+1]-a[i]>=0&&min1[i]+(a[n]-a[i])>=0&&a[n]==0) 34 res++; 35 return res; 36 //程序一开始的时候就判断了a[n]!=0的情况 所以这里不写其实也可以 37 } 38 int main() 39 { 40 scanf("%d",&n); 41 scanf("%s",s+1); 42 int cnt1=0,cnt2=0; 43 for(int i=1;i<=n;i++) 44 { 45 if(s[i]=='(') cnt1++; 46 else cnt2++; 47 } 48 if(cnt1!=cnt2) 49 { 50 puts("0 1 1"); 51 return 0; 52 } 53 ans=f(),l=1,r=1; 54 for(int i=1;i<=n;i++) 55 for(int j=i+1;j<=n;j++) 56 { 57 if(s[i]==s[j]) continue; 58 swp(i,j); 59 int res=f(); 60 if(ans<res) ans=res,l=i,r=j; 61 swp(i,j); 62 } 63 printf("%d %d %d ",ans,l,r); 64 return 0; 65 }
