calc
【问题描述】
一个序列a1,...,an是合法的,当且仅当:
长度为给定的n。
a1,...,an都是[1,A]中的整数。
a1,...,an互不相等。
一个序列的值定义为它里面所有数的乘积,即a1a2...an。
求所有不同合法序列的值的和。
两个序列不同当且仅当他们任意一位不一样。
输出答案对一个数mod取余的结果。
【输入格式】
一行3个数,A,n,mod。意义为上面所说的。
【输出格式】
一行结果。
【样例输入】
9 7 10007
【样例输出】
3611
HINT
【数据规模】
0:A<=10,n<=10。
1..3:A<=1000,n<=20。
4..9:A<=10^9,n<=20。
10..19:A<=10^9,n<=500。。
全部:mod<=10^9,并且mod为素数,mod>A>n+1。
题解:
设 f[i][j] 为用不大于A的数组成的有序合法序列方案数
转移方程:(是否选取 i 这个数字)
![]()
题目要求无序,那么最后乘上 n! 即可
细心观察一小下,发现它是一个有 2n 项的多项式
用拉格朗日插值法:
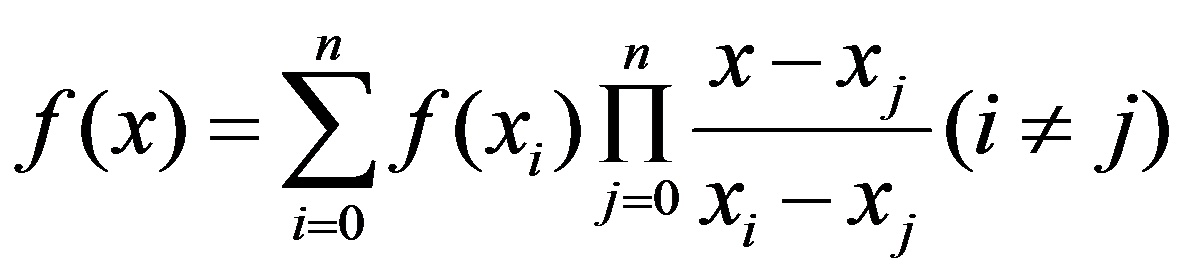
1 #include<cmath> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<algorithm> 7 using namespace std; 8 typedef long long lo; 9 inline int Get() 10 { 11 int x; 12 char c; 13 bool o = false; 14 while((c = getchar()) < '0' || c > '9') 15 if(c == '-') o = true; 16 x = c - '0'; 17 while((c = getchar()) >= '0' && c <= '9') 18 x = x * 10 + c - '0'; 19 return (o) ? -x : x; 20 } 21 const int maxn = 2333; 22 int f[maxn][maxn]; 23 int fac[maxn]; 24 int x[maxn], y[maxn]; 25 int a, n, m, mo; 26 int z, v, ans; 27 int num; 28 inline void Dp() 29 { 30 f[0][0] = 1; 31 for(int i = 1; i <= m; ++i) 32 for(int j = 0; j <= n; ++j) 33 { 34 f[i][j] = f[i - 1][j]; 35 if(j) f[i][j] += (lo) f[i - 1][j - 1] * i % mo; 36 if(f[i][j] >= mo) f[i][j] -= mo; 37 } 38 } 39 inline void Fac() 40 { 41 fac[0] = 1; 42 for(int i = 1; i <= n; ++i) fac[i] = (lo) fac[i - 1] * i % mo; 43 } 44 inline void Sun() 45 { 46 num = 0; 47 for(int i = 0; i <= m; ++i) 48 if(f[i][n]) 49 { 50 x[++num] = i, y[num] = f[i][n]; 51 if(num == (n << 1 | 1)) return; 52 } 53 } 54 inline int Mod(int x) 55 { 56 if(x < 0) x += mo; 57 return x; 58 } 59 inline int Pow(int x, int n) 60 { 61 int sum = 1; 62 while(n) 63 { 64 if(n & 1) sum = (lo) sum * x % mo; 65 x = (lo) x * x % mo; 66 n >>= 1; 67 } 68 return sum; 69 } 70 int main() 71 { 72 a = Get(), n = Get(), mo = Get(); 73 m = n << 2; 74 Dp(); 75 Fac(); 76 if(m >= a) 77 { 78 printf("%d", (lo) f[a][n] * fac[n] % mo); 79 return 0; 80 } 81 Sun(); 82 z = 1; 83 for(int i = 1; i <= num; ++i) z = (lo) z * Mod(a - x[i]) % mo; 84 for(int i = 1; i <= num; ++i) 85 { 86 v = Mod(a - x[i]); 87 for(int j = 1; j <= num; ++j) 88 if(i != j) 89 v = (lo) v * Mod(x[i] - x[j]) % mo; 90 ans = ans + (lo) y[i] * z % mo * Pow(v, mo - 2) % mo; 91 if(ans >= mo) ans -= mo; 92 } 93 printf("%d", (lo) ans * fac[n] % mo); 94 }