Gate Of Babylon
【问题描述】

【输入格式】

【输出格式】

【样例输入】
2 1 10 13
3
【样例输出】
12
【样例说明】

【数据范围】
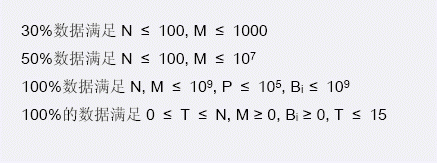
题解:
答案为全部没有限制的方案-有一个超过限制的方案数+有两个超过限制的方案数-有三个超过限制的方案数······
解释一下:
我们先算出所有的方案数,减去每一种超级神器超过限制的方案
而这其中有同时两种神器都都不满足条件的方案
这种方案被减了两次
那么加上有两个超过限制的方案数
有两个超过限制的方案数中有三种同时超过限制的方案数
并且有一种超过限制的方案数中又含有了有三种同时超过的方案数
那么再减去有三种超过限制的方案数
接下来同理······
我们发现答案式子中有奇数个超过限制的方案数为减法,而有偶数个超过限制的方案数为加法
考虑直接Dfs
n组无限制的数中选m个的方案数:C(n+m-1,m)
那么不超过m个的方案数为:C(n+0-1,0)+C(n+1-1,1)+C(n+2-1,2)+···+C(n+m-1,m)=C(n+m,m) (C(n,m)=C(n-1,m-1)+C(n-1,m))
Lucas定理:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 #include<cmath>
7 using namespace std;
8 long long n, m, t, p;
9 inline int Get()
10 {
11 int x = 0;
12 char c = getchar();
13 while('0' > c || c > '9') c = getchar();
14 while('0' <= c && c <= '9')
15 {
16 x = (x << 3) + (x << 1) + c - '0';
17 c = getchar();
18 }
19 return x;
20 }
21 inline long long Pow(long long m, long long n)
22 {
23 long long res = 1;
24 long long sum = m;
25 while(n)
26 {
27 if(n & 1) res = (res * sum) % p;
28 sum = (sum % p * sum % p) % p;
29 n >>= 1;
30 }
31 return res;
32 }
33 long long ans;
34 long long c[100233];
35 long long su[100233];
36 inline long long Zhs(long long a, long long b)
37 {
38 if(a < b) return 0;
39 return ((su[a] % p) * Pow((su[b] % p) * (su[a - b] % p) % p, p - 2)) % p;
40 }
41 inline long long Lu(long long a, long long b)
42 {
43 if(a < b) return 0;
44 long long res = 1;
45 while(a && b)
46 {
47 res = (res * Zhs(a % p, b % p)) % p;
48 a /= p;
49 b /= p;
50 }
51 return res;
52 }
53 void Dfs(int x, long long o, long long w)
54 {
55 if(x == t + 1)
56 {
57 ans = ((ans + o * (Lu(m + n - w, m - w) % p)) % p + p) % p;
58 return;
59 }
60 Dfs(x + 1, o, w);
61 Dfs(x + 1, -o, w + c[x] + 1);
62 }
63 int main()
64 {
65 n = Get(), t = Get(), m = Get(), p = Get();
66 for(int i = 1; i <= t; ++i) c[i] = Get();
67 su[0] = 1;
68 for(int i = 1; i <= p; ++i) su[i] = (su[i - 1] * i) % p;
69 Dfs(1, 1, 0);
70 printf("%lld", ans);
71 }