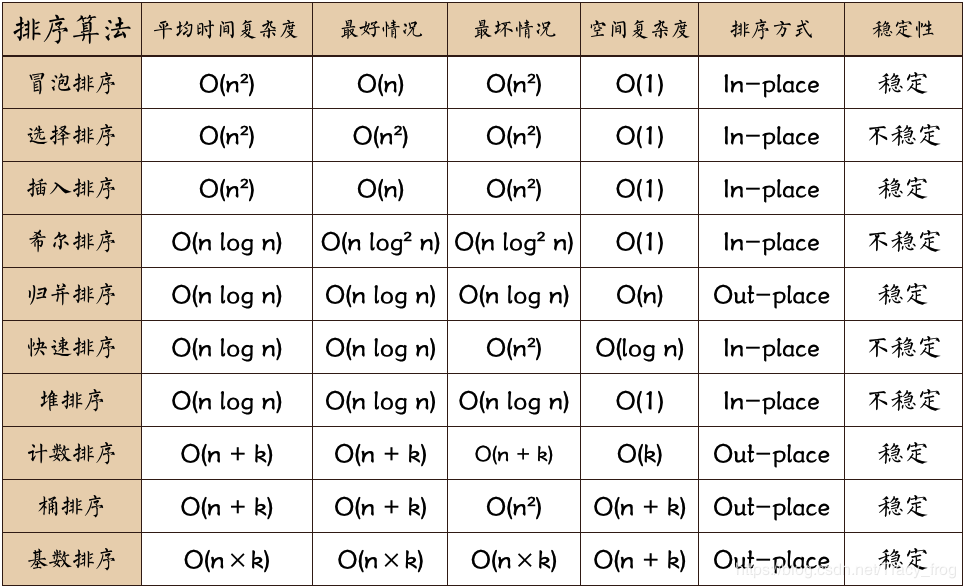
相关概念
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
一、冒泡排序
//冒泡排序
function bubbleSort (arr) {
let len = arr.length
for (var i = 0; i < len-1; i++){ //控制外层循环次数
for(var j = 0; j < len-i-1; j++) { //控制每个数的比较次数
if(arr[j] > arr[j+1]) {
console.log('>>>>>>')
let temp = arr[j+1]
arr[j+1] = arr[j]
arr[j] = temp
}
}
}
return arr
}
let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46];
console.log('arr :', bubbleSort(arr));
二、选择排序
function selectSort(arr){
let len = arr.length
let minIndex ,temp
for(let i = 0; i < len - 1; i++) {
minIndex = i //默认最小值
for (let j = i+1; j < len; j++) {
if(arr[j] < arr[j+1]) { //寻找最小值
minIndex = j //最小值的索引
}
}
//交换默认最小值和最小值的位置
temp = arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = temp
}
}
三、插入排序
function insertSort (arr) {
let len = arr.length
let preIndex, current
for(let i = 1; i < len; i++) {
preIndex = i-1
current = arr[i]
//结束的条件是找到已排序的元素小于或者等于当前元素的位置
while(preIndex >= 0 && arr[preIndex] > current) { //如果前面的数大于当前元素,
arr[preIndex+1] = arr[preIndex] //就将前一个数向后移
preIndex-- //指针向前移动
}
//将当前元素插入到该位置后
arr[preIndex+1] = current
}
}
思路:
1、选择数组中间数作为基数,并从数组中取出此基数;
2、准备两个数组容器,遍历数组,逐个与基数比对,较小的放左边容器,较大的放右边容器;
3、递归处理两个容器的元素,并将处理后的数据与基数按大小合并成一个数组,返回。
实现:
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
总结:
R的思路非常清晰,选择基数为参照,划分数组,分而治之,对于新手来理解快排的核心思想“参照-划分-递归”,很容易理解 。
既实现了排序,又符合快速排序的思想,为什么还会为人所诟病呢?原来是因为:
1、R取基数用的是splice()函数取,而不是算法中常用的取下标。基数只是一个参照对象,在比对的时候,只要能从数组中取到即可,所以只需要知道它的索引即可,调用函数删除基数只会更耗时;
2、根据基数来划分时,R专门生成两个数组来存储,从而占用了更多的存储空间(增加了空间复杂度)。
严格上讲,R的代码仅仅是用快速排序的思想实现了排序,也算是快速排序,但是还有很多改进之处。
二、某乎上的解法
基本思路跟我上述理解大同小异,主要来看看这篇文章具体的实现过程。下面借用原文的图来讲解(原文的图做的很好就不单独画图了,主要讲一讲原文没解释需要注意的地方,和对该篇文章做一个补充),底部附原文链接。
1.数组[2,3,1,5,6,4],创建两指针,一个只想头一个指向尾,再确定一个基准数。
(注意:为了方便后面递归是能够确定基准数,这里基准数选取,第一个数或者最后一个数)

2.开始第一次的递归处理,尾指针先从右往左扫,扫到第一个小于(注意是小于,而不是小于等于哦)基准数的位置停住,这时候头指针再从左往右扫,扫到第一个大于基准数的位置停住,这时候是下面的图示状态:
(注意:这里如果基准数选区的第一个数,应该尾指针先往左侧扫,若基准数选取为最后一个属则,应是头指针向往右扫)
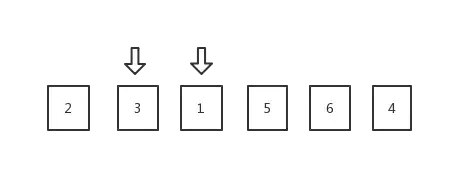
交换两个指针所指的数,成为了下面的状态:
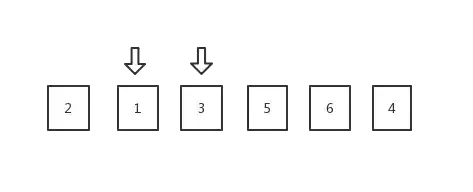
3.两个数交换完毕,右指针此时指的是arr[2] = 3, 左指针指着arr[1] = 1;交换完毕后右指针继续从当前位置往左扫,扫到1的时候发现和左指针相遇了,那么这个时候就结束左右指针的扫描,左右指针同时指着arr[1] = 1,即:
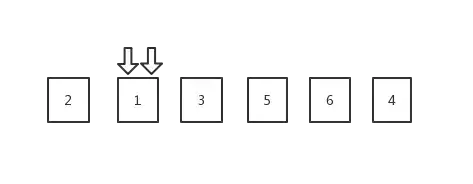
此时退出循环扫描的过程,交换基准数与左右指针同时所指的数的位置,开头说了,基准数我选择的是arr[0] = 2, 指针指的是arr[1] = 1; 交换过后就变成了:

这时候就发现基准数已经出现在了它排完序后应该在的位置(排完序后是[1,2,3,4,5,6],2出现在了第2位),比这个基准数小的数组出现在了它的左边([1]出现在了2的左边),比基准数大的出现在了它的右边([3,5,6,4]出现在了2的右边)。
4.之后的过程就是对左右数组的分别递归处理。
let quickSort = (arr, begin, end) => {
//递归出口
if (begin >= end)
return;
var l = begin; // 左指针
var r = end; //右指针
var temp = arr[begin]; //基准数,这里取数组第一个数
//左右指针相遇的时候退出扫描循环
while (l < r) {
//右指针从右向左扫描,碰到第一个小于基准数的时候停住
while (l < r && arr[r] >= temp)
r--;
//左指针从左向右扫描,碰到第一个大于基准数的时候停住
while (l < r && arr[l] <= temp)
l++;
//交换左右指针所停位置的数
[arr[l], arr[r]] = [arr[r], arr[l]];
}
//最后交换基准数与指针相遇位置的数
[arr[begin], arr[l]] = [arr[l], arr[begin]];
//递归处理左右数组
quickSort(arr, begin, l - 1);
quickSort(arr, l + 1, end);
};
let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46];
let end = arr.length-1
console.log('arr :', quickSort(arr, 0, end));
推荐比较好的几篇文章
https://zhuanlan.zhihu.com/p/93129029
https://www.cnblogs.com/siegaii/p/10744645.html