1. 使用策略
分治策略
2. 优点
在原址排序,空间复杂度低;
3. 复杂度
时间复杂度:
最优O(nlgn) 最坏O(n^2) 平均O(nlgn)
空间复杂度:
最优O(lgn) 最坏O(n) 平均(lgn)
4. 算法解析
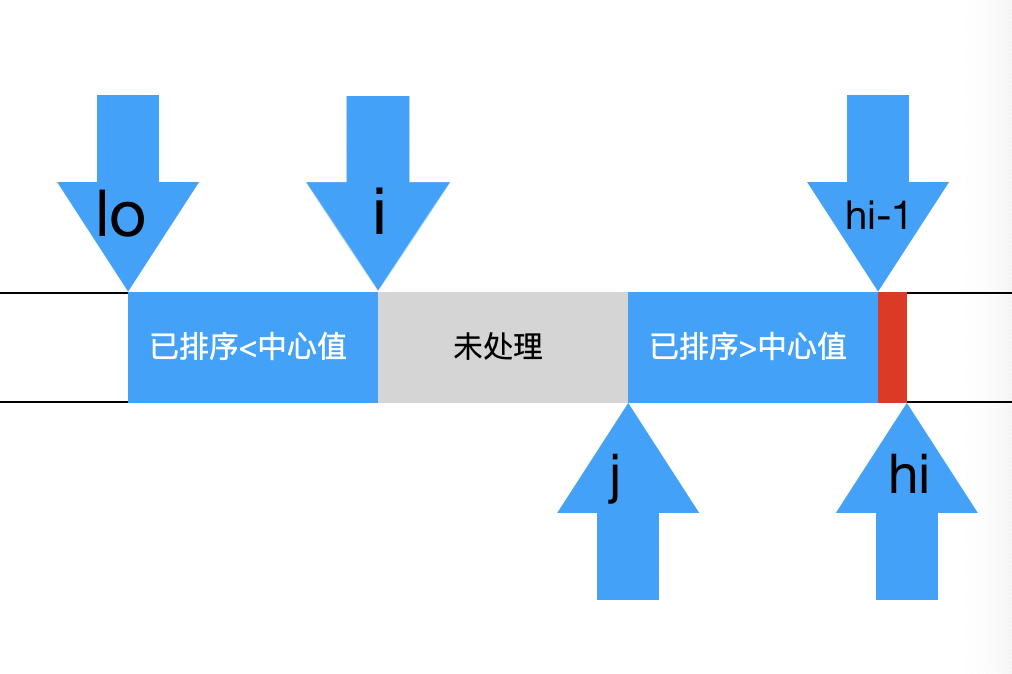
关键:将数组按照某个中心值进行分割;中心值左侧均小于中心值,中心值右侧均大于中心值;
方法(partition):
1. 设两个边界值,来表示数组的索引区间;[lo, hi)=>lo=0, hi=A.length
2. 将数组最后一个值设为中心值
3. 左侧设一个遍历索引,从i=0开始遍历;
如果A[i]比中心值大,和右侧开始遍历的值交换,然后再次比较该位置的值和中心值的大小;
否则移动遍历索引,相当于将其归入已排序子数组[lo, i)。
4. 右侧设一个遍历索引j, 每次被交换后,j向前移动一位,遍历后的数组归为[j,hi-1);
5. 当i===j时,遍历结束;因为j位于第二个区间,则将其与最后的中心值交换;返回j
6. 左右两侧的子数组递归调用该方法
代码实现:
function swap(A, i, j) {// 比[a,b]=[b,a]效率高 let temp = A[i]; A[i] = A[j]; A[j] = temp; } //返回中心值最后所在位置;同时已经排序 function partition(A, lo, hi) { const pivot = A[hi-1]; let i = lo, j = hi-1; while(i!==j) { if (A[i] < pivot) { i++; } else { swap(A, i, --j); } } swap(A, j, hi-1); return j; } function qsort(A, lo=0, hi=A.length) { if(hi-lo <=1) return; const p = partition(A,lo,hi); qsort(A, lo, p); qsort(A, p+1, hi); }
代码测试:
const A = [12,65,10,45,34,89,56]; qsort(A); console.log(A); // 打印结果 [10, 12, 34, 45, 56, 65, 89]