公元五八○一年,地球居民迁移至金牛座α第二行星,在那里发表银河联邦
创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历七九九年,银河系的两大军事集*在巴米利恩星域爆发战争。泰山压
顶集**宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集*点名将杨
威利组织麾下三万艘战舰迎敌。
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在
这次决战中,他将巴米利恩星域战场划分成30000列,每列依次编号为1, 2, …,
30000。之后,他把自己的战舰也依次编号为1, 2, …, 30000,让第i号战舰处于
第i列(i = 1, 2, …, 30000),形成“一字长蛇阵”,诱敌深入。这是初始阵形。当
进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,
实施密集攻击。合并指令为M i j,含义为让第i号战舰所在的整个战舰队列,作
为一个整体(头在前尾在后)接至第j号战舰所在的战舰队列的尾部。显然战舰
队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增
大。 然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通
过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战
舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利
的第i号战舰与第j号战舰当前是否在同一列中,如果在同一列中,那么它们之
间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以
及回答莱因哈特的询问。
最终的决战已经展开,银河的历史又翻过了一页……
输入输出格式
输入格式:输入文件galaxy.in的第一行有一个整数T(1<=T<=500,000),表示总共有T
条指令。
以下有T行,每行有一条指令。指令有两种格式:
- M i j :i和j是两个整数(1<=i , j<=30000),表示指令涉及的战舰编号。
该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第i号战
舰与第j号战舰不在同一列。
- C i j :i和j是两个整数(1<=i , j<=30000),表示指令涉及的战舰编号。
该指令是莱因哈特发布的询问指令。
输出格式:输出文件为galaxy.out。你的程序应当依次对输入的每一条指令进行分析和
处理:
如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序
要注意到这一点,但是不要输出任何信息;
如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,
表示在同一列上,第i 号战舰与第j 号战舰之间布置的战舰数目。如果第i 号战
舰与第j号战舰当前不在同一列上,则输出-1。
输入输出样例
4 M 2 3 C 1 2 M 2 4 C 4 2
-1 1
说明
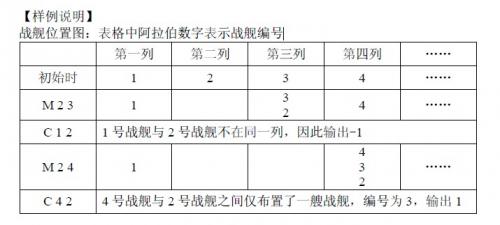
【样例说明】
战舰位置图:表格中阿拉伯数字表示战舰编号
感觉挺对,然而对于测试数据,会多次死循环:
/*
银河
4
M 2 3
C 1 2
M 2 4
C 4 2
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=30010;
int root[N],child[N];//路径压缩
int fa[N],son[N];//直系
char how;
int l,r;
inline int read()
{
int x=0;int f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
return x*f;
}
int getroot(int x)
{
return root[x]==x?x:root[x]=getroot(root[x]);
}
int getchild(int x)
{
return child[x]==x?x:child[x]=getchild(child[x]);
}
inline bool jud(int l,int r)
{
int tot=0;
while(son[r]!=r)
{
tot++;
if(tot>=5000)return 1;
if(r==l)
return 1;
r=son[r];
}
return 0;
}
int main()
{
//freopen("sad.out","w",stdout);
for(int i=1;i<N;i++)
root[i]=child[i]=fa[i]=son[i]=i;
int T;
T=read();
for(int i=1;i<=T;i++)
{
scanf("%c",&how);
l=read(),r=read();//l 或者 r 所在的那一列
int rootl,rootr,childr;
if(how=='M')
{
rootl=getroot(l);
childr=getchild(r);
fa[rootl]=childr;
son[childr]=rootl;
root[rootl]=childr;
}
else
{
rootl=getroot(l);
rootr=getroot(r);
if(rootl!=rootr)
printf("-1
");
else
{
if(jud(l,r))
swap(l,r);
int answer(0);
while(l!=r)
answer++,
l=son[l];
printf("%d
",answer-1);
}
}
}
return 0;
}
/*
10
M 3 4
M 3 5
M 1 2
M 1 3
C 3 1
C 5 1
C 3 4
C 3 5
C 5 1
C 4 2
*/
AC:
#include<bits/stdc++.h>
using namespace std;
int fa[30001],front[30001],num[30001],x,y,i,j,n,T,ans;
//fa[i]表示飞船i的祖先
//front[i]表示飞船i与其所在列队头的距离
//num[i]表示第i列的飞船数量
char ins;
int find(int n)
{ //查找祖先的函数
if(fa[n]==n)return fa[n];
int fn=find(fa[n]); //先递归找到祖先
front[n]+=front[fa[n]]; //在回溯的时候更新front(因为更新时要用到正确的front[祖先],
//所以只能在回溯的时候更新)
return fa[n]=fn;
}
int main()
{
cin>>T;
for(i=1;i<=30000;++i)
{ //定初值
fa[i]=i;
front[i]=0;
num[i]=1;
}
while(T--)
{
cin>>ins>>x>>y;
int fx=find(x); //fx为x所在列的队头
int fy=find(y); //fy同上
if(ins=='M')
{
front[fx]+=num[fy]; //更新front[x所在列队头(现在在y所在队列后面)]
//即加上y所在队列的长度
fa[fx]=fy; //将fy设为fx的祖先
num[fy]+=num[fx]; //更新以fy为队头队列的长度
num[fx]=0; //以fx为队头的队列已不存在,更新
}
if(ins=='C')
{
if(fx!=fy)cout<<"-1"<<endl; //若x和y的祖先不相同,则不在同一列
else cout<<abs(front[x]-front[y])-1<<endl; //否则利用x和y离队头的距离算
//出它们的距离
}
}
return 0;
}