分类和回归

引自：https://www.cnblogs.com/zhoubindut/p/12142186.html

上篇文章中，我们就机器学习的相关基础概念进行了阐述，包括机器学习的基本概念以及机器学习的分类。不了解的童鞋可以看一下补补课,机器学习系列（一）——基础概念及分类。
分类和回归问题作为典型的机器学习问题，一直困扰了我很久，在查了好多文献和推文后，整理下来下面的文档，希望可以帮助大家，更加细致全面的了解这两种算法。

​ 分类算法和回归算法的区别：

​ 分类算法和回归算法是对真实世界不同建模的方法。分类模型是认为模型的输出是离散的，例如大自然的生物被划分为不同的种类，是离散的。回归模型的输出是连续的，例如人的身高变化过程是一个连续过程，而不是离散的。

​ 因此，在实际建模过程时，采用分类模型还是回归模型，取决于你对任务（真实世界）的分析和理解。

3 分类算法

3.1 常用分类算法的优缺点？

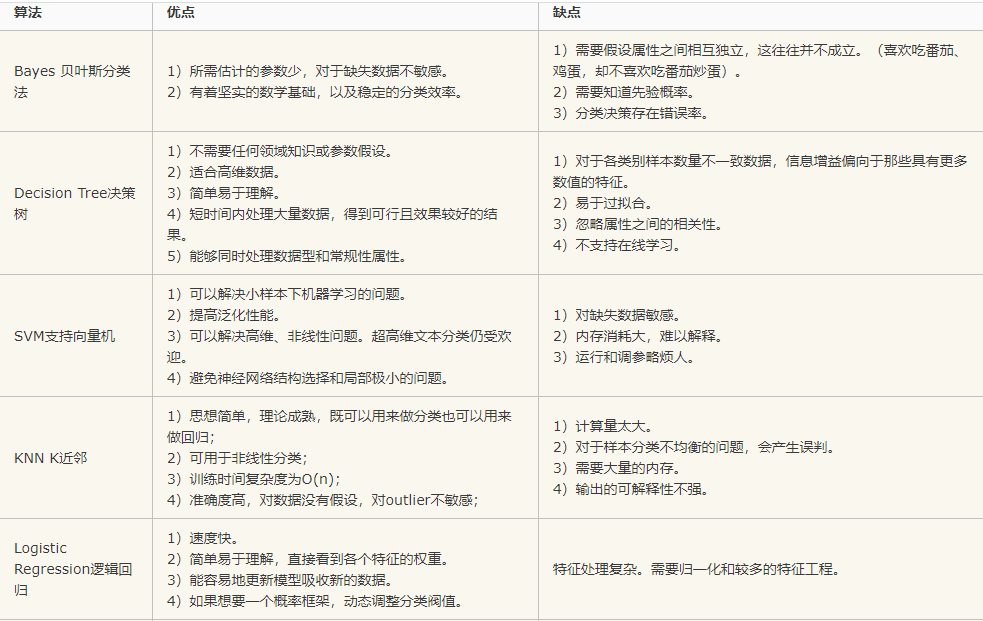
​ 接下来首先介绍常用分类算法的优缺点，如表2-1所示。

​ 表2-1 常用分类算法的优缺点

 

3.2 分类算法的评估方法

​ 分类评估方法主要功能是用来评估分类算法的好坏，而评估一个分类器算法的好坏又包括许多项指标。了解各种评估方法，在实际应用中选择正确的评估方法是十分重要的。

• 几个常用术语
  ​ 这里首先介绍几个常见的模型评价术语，现在假设我们的分类目标只有两类，计为正例（positive）和负例（negative）分别是：

  1. True positives(TP): 被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数；
  2. False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
  3. False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
  4. True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。　 ​
     四个术语组成混淆矩阵：
     1）P=TP+FN表示实际为正例的样本个数。
     2）True、False描述的是分类器是否判断正确。
     3）Positive、Negative是分类器的分类结果，如果正例计为1、负例计为-1，即positive=1、negative=-1。用1表示True，-1表示False，那么实际的类标=TF*PN，TF为true或false，PN为positive或negative。
     4）例如True positives(TP)的实际类标=1*1=1为正例，False positives(FP)的实际类标=(-1)*1=-1为负例，False negatives(FN)的实际类标=(-1)*(-1)=1为正例，True negatives(TN)的实际类标=1*(-1)=-1为负例。

• 评价指标

  1. 正确率（accuracy）
     正确率是我们最常见的评价指标，accuracy = (TP+TN)/(P+N)，正确率是被分对的样本数在所有样本数中的占比，通常来说，正确率越高，分类器越好。
  2. 错误率（error rate)
     错误率则与正确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(P+N)，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。
  3. 灵敏度（sensitivity）
     sensitivity = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。
  4. 特异性（specificity)
     specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。
  5. 精度（precision）
     precision=TP/(TP+FP)，精度是精确性的度量，表示被分为正例的示例中实际为正例的比例。
  6. 召回率（recall）
     召回率是覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitivity，可以看到召回率与灵敏度是一样的。
  7. 其他评价指标
     计算速度：分类器训练和预测需要的时间；评估速度的常用指标是每秒帧率（Frame Per Second，FPS），即每秒内可以处理的图片数量。当然要对比FPS，你需要在同一硬件上进行。另外也可以使用处理一张图片所需时间来评估检测速度，时间越短，速度越快。
     鲁棒性：处理缺失值和异常值的能力；
     可扩展性：处理大数据集的能力；
     可解释性：分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。
  8. 精度和召回率反映了分类器分类性能的两个方面。如果综合考虑查准率与查全率，可以得到新的评价指标F1-score，也称为综合分类率：F1=2×precision×recallprecision+recallF1=2×precision×recallprecision+recall。

  为了综合多个类别的分类情况，评测系统整体性能，经常采用的还有微平均F1（micro-averaging）和宏平均F1（macro-averaging ）两种指标。

  （1）宏平均F1与微平均F1是以两种不同的平均方式求的全局F1指标。

  （2）宏平均F1的计算方法先对每个类别单独计算F1值，再取这些F1值的算术平均值作为全局指标。

  （3）微平均F1的计算方法是先累加计算各个类别的a、b、c、d的值，再由这些值求出F1值。

  （4）由两种平均F1的计算方式不难看出，宏平均F1平等对待每一个类别，所以它的值主要受到稀有类别的影响，而微平均F1平等考虑文档集中的每一个文档，所以它的值受到常见类别的影响比较大。

• ROC曲线和PR曲线

  ROC曲线是（Receiver Operating Characteristic Curve，受试者工作特征曲线）的简称，是以灵敏度（真阳性率）为纵坐标，以1减去特异性（假阳性率）为横坐标绘制的性能评价曲线。可以将不同模型对同一数据集的ROC曲线绘制在同一笛卡尔坐标系中，ROC曲线越靠近左上角，说明其对应模型越可靠。也可以通过ROC曲线下面的面积（Area Under Curve, AUC）来评价模型，AUC越大，模型越可靠。

  PR曲线是Precision Recall Curve的简称，描述的是precision和recall之间的关系，以recall为横坐标，precision为纵坐标绘制的曲线。该曲线的所对应的面积AUC实际上是目标检测中常用的评价指标平均精度（Average Precision, AP）。AP越高，说明模型性能越好。 mAP 即 Mean Average Precision即平均AP值，是对多个验证集个体求平均AP值，作为 object dection中衡量检测精度的指标。

图像目标检测的IOU是什么？

IoU 作为目标检测算法性能 mAP 计算的一个非常重要的函数。IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。

3.3 正确率能很好的评估分类算法吗

​ 不同算法有不同特点，在不同数据集上有不同的表现效果，根据特定的任务选择不同的算法。如何评价分类算法的好坏，要做具体任务具体分析。对于决策树，主要用正确率去评估，但是其他算法，只用正确率能很好的评估吗？
​ 答案是否定的。
​ 正确率确实是一个很直观很好的评价指标，但是有时候正确率高并不能完全代表一个算法就好。比如对某个地区进行地震预测，地震分类属性分为0：不发生地震、1发生地震。我们都知道，不发生的概率是极大的，对于分类器而言，如果分类器不加思考，对每一个测试样例的类别都划分为0，达到99%的正确率，但是，问题来了，如果真的发生地震时，这个分类器毫无察觉，那带来的后果将是巨大的。很显然，99%正确率的分类器并不是我们想要的。出现这种现象的原因主要是数据分布不均衡，类别为1的数据太少，错分了类别1但达到了很高的正确率缺忽视了研究者本身最为关注的情况。

3.4 什么样的分类器是最好的

​ 对某一个任务，某个具体的分类器不可能同时满足或提高所有上面介绍的指标。
​ 如果一个分类器能正确分对所有的实例，那么各项指标都已经达到最优，但这样的分类器往往不存在。比如之前说的地震预测，既然不能百分百预测地震的发生，但实际情况中能容忍一定程度的误报。假设在1000次预测中，共有5次预测发生了地震，真实情况中有一次发生了地震，其他4次则为误报。正确率由原来的999/1000=99.9下降为996/1000=99.6。召回率由0/1=0%上升为1/1=100%。对此解释为，虽然预测失误了4次，但真的地震发生前，分类器能预测对，没有错过，这样的分类器实际意义更为重大，正是我们想要的。在这种情况下，在一定正确率前提下，要求分类器的召回率尽量高。

4 逻辑回归

4.1 回归划分

广义线性模型家族里，依据因变量不同，可以有如下划分：

（1）如果是连续的，就是多重线性回归。

（2）如果是二项分布，就是逻辑回归。

（3）如果是泊松（Poisson）分布，就是泊松回归。

（4）如果是负二项分布，就是负二项回归。

（5）逻辑回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的逻辑回归。

4.2 逻辑回归适用性

逻辑回归可用于以下几个方面：

（1）用于概率预测。用于可能性预测时，得到的结果有可比性。比如根据模型进而预测在不同的自变量情况下，发生某病或某种情况的概率有多大。

（2）用于分类。实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。进行分类时，仅需要设定一个阈值即可，可能性高于阈值是一类，低于阈值是另一类。

（3）寻找危险因素。寻找某一疾病的危险因素等。

（4）仅能用于线性问题。只有当目标和特征是线性关系时，才能用逻辑回归。在应用逻辑回归时注意两点：一是当知道模型是非线性时，不适用逻辑回归；二是当使用逻辑回归时，应注意选择和目标为线性关系的特征。

（5）各特征之间不需要满足条件独立假设，但各个特征的贡献独立计算。

4.3 逻辑回归与朴素贝叶斯有什么区别

逻辑回归与朴素贝叶斯区别有以下几个方面：

（1）逻辑回归是判别模型， 朴素贝叶斯是生成模型，所以生成和判别的所有区别它们都有。

（2）朴素贝叶斯属于贝叶斯，逻辑回归是最大似然，两种概率哲学间的区别。

（3）朴素贝叶斯需要条件独立假设。

（4）逻辑回归需要求特征参数间是线性的。