计算机视觉任务主要分为:分类、检测、识别、定位四大类。
L1 loss ,L2 loss和smooth L1 loss
引自:https://cloud.tencent.com/developer/article/1441560 https://blog.csdn.net/qq_26598445/article/details/82844393
一、常见的MSE、MAE损失函数
1.1 均方误差、平方损失
均方误差(MSE)是回归损失函数中最常用的误差,它是预测值与目标值之间差值的平方和,其公式如下所示:

下图是均方根误差值的曲线分布,其中最小值为预测值为目标值的位置。我们可以看到随着误差的增加损失函数增加的更为迅猛。

优点:各点都连续光滑,方便求导,具有较为稳定的解
缺点:不是特别的稳健,为什么?因为当函数的输入值距离中心值较远的时候,使用梯度下降法求解的时候梯度很大,可能导致梯度爆炸
1.2 平均绝对误差
平均绝对误差(MAE)是另一种常用的回归损失函数,它是目标值与预测值之差绝对值的和,表示了预测值的平均误差幅度,而不需要考虑误差的方向(注:平均偏差误差MBE则是考虑的方向的误差,是残差的和),范围是0到∞,其公式如下所示:


优点:无论对于什么样的输入值,都有着稳定的梯度,不会导致梯度爆炸问题,具有较为稳健性的解
缺点:在中心点是折点,不能求导,不方便求解
备注:上面的两种损失函数也被很多资料或者是教材称之为
L2损失和L1损失,但是本文还是将它们跟下面的L1损失和L2损失进行区分了的。
二、L1_Loss和L2_Loss
2.1 L1_Loss和L2_Loss的公式
L1范数损失函数,也被称为最小绝对值偏差(LAD),最小绝对值误差(LAE)。总的说来,它是把目标值(Yi)与估计值(f(xi))的绝对差值的总和(S)最小化:

L2范数损失函数,也被称为最小平方误差(LSE)。总的来说,它是把目标值(Yi)与估计值(f(xi))的差值的平方和(S)最小化:

L1范数与L2范数作为损失函数的区别能快速地总结如下:
|
L2损失函数 |
L1损失函数 |
|---|---|
|
不是非常的鲁棒(robust) |
鲁棒 |
|
稳定解 |
不稳定解 |
|
总是一个解 |
可能多个解 |
总结:实际上我们发现,其实所谓的L1_Loss与L2_Loss与前面说的MSE、MAE损失函数一个1/n的区别,所以他们的优点和缺点是互通的。
2.2 几个关键的概念
(1)鲁棒性(robustness)
因为与最小平方相比,最小绝对值偏差方法的鲁棒性更好,因此,它在许多场合都有应用。最小绝对值偏差之所以是鲁棒的,是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值,那么最小绝对值偏差是更好的选择。
从直观上说,因为L2范数将误差平方化(如果误差大于1,则误差会放大很多),模型的误差会比L1范数来得大,因此模型会对这个样本更加敏感,这就需要调整模型来最小化误差。如果这个样本是一个异常值,模型就需要调整以适应单个的异常值,这会牺牲许多其它正常的样本,因为这些正常样本的误差比这单个的异常值的误差小。
(2)稳定性
最小绝对值偏差方法的不稳定性意味着,对于数据集的一个小的水平方向的波动,回归线也许会跳跃很大。在一些数据结构(data configurations)上,该方法有许多连续解;但是,对数据集的一个微小移动,就会跳过某个数据结构在一定区域内的许多连续解。(The method has continuous solutions for some data configurations; however, by moving a datum a small amount, one could “jump past” a configuration which has multiple solutions that span a region. )在跳过这个区域内的解后,最小绝对值偏差线可能会比之前的线有更大的倾斜。相反地,最小平方法的解是稳定的,因为对于一个数据点的任何微小波动,回归线总是只会发生轻微移动;也就说,回归参数是数据集的连续函数。
三、smooth L1损失函数
其实顾名思义,smooth L1说的是光滑之后的L1,前面说过了L1损失的缺点就是有折点,不光滑,那如何让其变得光滑呢?
smooth L1损失函数为:

smooth L1损失函数曲线如下图所示,作者这样设置的目的是想让loss对于离群点更加鲁棒,相比于L2损失函数,其对离群点(指的是距离中心较远的点)、异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞。

smooth L1损失函数曲线
总结:从上面可以看出,该函数实际上就是一个分段函数,在[-1,1]之间实际上就是L2损失,这样解决了L1的不光滑问题,在[-1,1]区间外,实际上就是L1损失,这样就解决了离群点梯度爆炸的问题。

三者一对比,各自的优缺点就一目了然了。
- 为什么L1正则会产生稀疏解呢?这里利用公式进行解释。
假设只有一个参数为w,损失函数为L(w),分别加上L1正则项和L2正则项后有:
假设L(w)在0处的倒数为d0,即
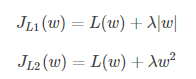
则可以推导使用L1正则和L2正则时的导数。
引入L2正则项,在0处的导数
引入L1正则项,在0处的导数
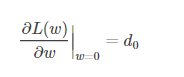
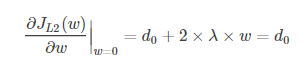

可见,引入L2正则时,代价函数在0处的导数仍是d0,无变化。而引入L1正则后,代价函数在0处的导数有一个突变。从d0+λ到d0−λ,若d0+λ和d0−λ异号,则在0处会是一个极小值点。因此,优化时,很可能优化到该极小值点上,即w=0处。
这里只解释了有一个参数的情况,如果有更多的参数,也是类似的。因此,用L1正则更容易产生稀疏解。