引自:https://zhuanlan.zhihu.com/p/36051603
1、对于具有更多层和节点的更大的神经网络,减少其存储和计算成本变得至关重要,特别是对于一些实时应用,如在线学习、增量学习以及自动驾驶。
2、在深度学习的另一端,即更贴近人们生活的移动端,如何让深度模型在移动设备上运行,也是模型压缩加速的一大重要目标。
当然,网络模型的压缩和加速的最终实现需要多学科的联合解决方案,除了压缩算法,数据结构、计算机体系结构和硬件设计等也起到了很大作用。本文将着重介绍不同的深度模型压缩方法,并进行对比。
研究现状
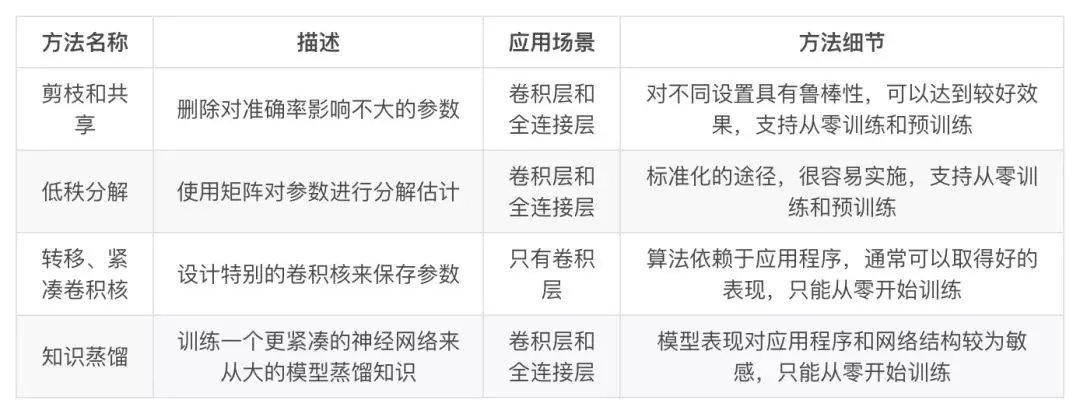
综合现有的深度模型压缩方法,它们主要分为四类:
- 参数修剪和共享(parameter pruning and sharing)
- 低秩因子分解(low-rank factorization)
- 转移/紧凑卷积滤波器(transferred/compact convolutional filters)
- 知识蒸馏(knowledge distillation)
基于参数修剪和共享的方法针对模型参数的冗余性,试图去除冗余和不重要的项。
基于低秩因子分解的技术使用矩阵/张量分解来估计深度学习模型的信息参数。
基于传输/紧凑卷积滤波器的方法设计了特殊的结构卷积滤波器来降低存储和计算复杂度。
知识蒸馏方法通过学习一个蒸馏模型,训练一个更紧凑的神经网络来重现一个更大的网络的输出。
一般来说,参数修剪和共享,低秩分解和知识蒸馏方法可以用于全连接层和卷积层的 CNN,但另一方面,使用转移/紧凑型卷积核的方法仅支持卷积层。低秩因子分解和基于转换/紧凑型卷积核的方法提供了一个端到端的流水线,可以很容易地在 CPU/GPU 环境中实现。相反参数修剪和共享使用不同的方法,如矢量量化,二进制编码和稀疏约束来执行任务,这导致常需要几个步骤才能达到目标。
1、参数修剪和共享
根据减少冗余(信息冗余或参数空间冗余)的方式,这些参数修剪和共享可以进一步分为三类:模型量化和二进制化、参数共享和结构化矩阵(structural matrix)。
量化和二进制化
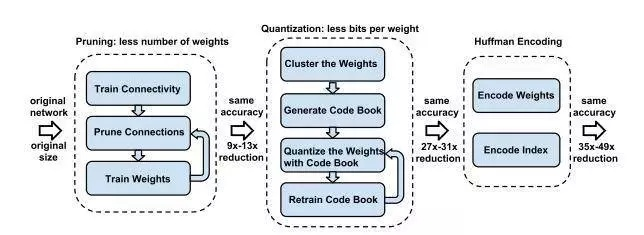
网络量化通过减少表示每个权重所需的比特数来压缩原始网络。Gong et al. 对参数值使用 K-Means 量化。Vanhoucke et al. 使用了 8 比特参数量化可以在准确率损失极小的同时实现大幅加速。Han S 提出一套完整的深度网络的压缩流程:首先修剪不重要的连接,重新训练稀疏连接的网络。然后使用权重共享量化连接的权重,再对量化后的权重和码本进行霍夫曼编码,以进一步降低压缩率。如图 2 所示,包含了三阶段的压缩方法:修剪、量化(quantization)和霍夫曼编码。
修剪减少了需要编码的权重数量,量化和霍夫曼编码减少了用于对每个权重编码的比特数。对于大部分元素为 0 的矩阵可以使用稀疏表示,进一步降低空间冗余,且这种压缩机制不会带来任何准确率损失。
在量化级较多的情况下准确率能够较好保持,但对于二值量化网络的准确率在处理大型 CNN 网络,如 GoogleNet 时会大大降低。另一个缺陷是现有的二进制化方法都基于简单的矩阵近似,忽视了二进制化对准确率损失的影响。
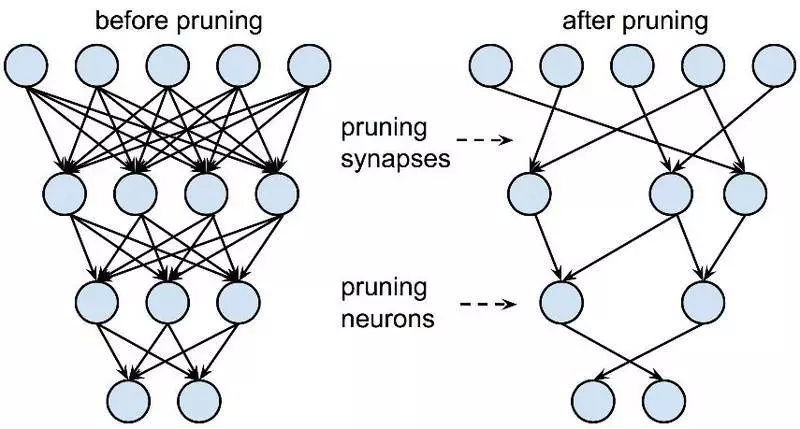
网络剪枝和共享起初是解决过拟合问题的,现在更多得被用于降低网络复杂度。
早期所应用的剪枝方法称为偏差权重衰减(Biased Weight Decay),其中最优脑损伤(Optimal Brain Damage)和最优脑手术(Optimal Brain Surgeon)方法,是基于损失函数的 Hessian 矩阵来减少连接的数量。他们的研究表明这种剪枝方法的精确度比基于重要性的剪枝方法(比如 Weight Decay 方法)更高。这个方向最近的一个趋势是在预先训练的 CNN 模型中修剪冗余的、非信息量的权重。
在稀疏性限制的情况下培训紧凑的 CNN 也越来越流行,这些稀疏约束通常作为 l_0 或 l_1 范数调节器在优化问题中引入。
剪枝和共享方法存在一些潜在的问题。首先,若使用了 l_0 或 l_1 正则化,则剪枝方法需要更多的迭代次数才能收敛,此外,所有的剪枝方法都需要手动设置层的超参数,在某些应用中会显得很复杂。
设计结构化矩阵
该方法的原理很简单:如果一个 m×n 阶矩阵只需要少于 m×n 个参数来描述,就是一个结构化矩阵(structured matrix)。通常这样的结构不仅能减少内存消耗,还能通过快速的矩阵-向量乘法和梯度计算显著加快推理和训练的速度。
这种方法的一个潜在的问题是结构约束会导致精确度的损失,因为约束可能会给模型带来偏差。另一方面,如何找到一个合适的结构矩阵是困难的。没有理论的方法来推导出来。因而该方法没有广泛推广。
2、低秩分解和稀疏性
一个典型的 CNN 卷积核是一个 4D 张量,而全连接层也可以当成一个 2D 矩阵,低秩分解同样可行。这些张量中可能存在大量的冗余。所有近似过程都是逐层进行的,在一个层经过低秩滤波器近似之后,该层的参数就被固定了,而之前的层已经用一种重构误差标准(reconstruction error criterion)微调过。这是压缩 2D 卷积层的典型低秩方法,如图 所示。
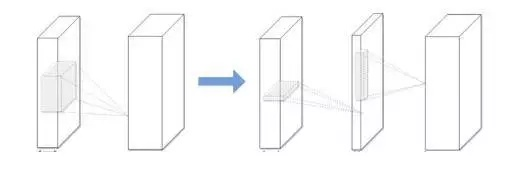
使用低阶滤波器加速卷积的时间已经很长了,例如,高维 DCT(离散余弦变换)和使用张量积的小波系统分别由 1D DCT 变换和 1D 小波构成。学习可分离的 1D 滤波器由 Rigamonti 等人提出,遵循字典学习的想法。Jaderberg 的工作提出了使用不同的张量分解方案,在文本识别准确率下降 1% 的情况下实现了 4.5 倍加速。
一种 flatten 结构将原始三维卷积转换为 3 个一维卷积,参数复杂度由 O(XYC)降低到O(X+Y+C),运算复杂度由 O(mnCXY) 降低到 O(mn(X+Y+C)。低阶逼近是逐层完成的。完成一层的参数确定后,根据重建误差准则对上述层进行微调。这些是压缩二维卷积层的典型低秩方法。
按照这个方向,Lebedev 提出了核张量的典型多项式(CP)分解,使用非线性最小二乘法来计算。Tai 提出了一种新的从头开始训练低秩约束 CNN 的低秩张量分解算法。它使用批量标准化(BN)来转换内部隐藏单元的激活。一般来说, CP 和 BN分解方案都可以用来从头开始训练 CNN。
低秩方法很适合模型压缩和加速,但是低秩方法的实现并不容易,因为它涉及计算成本高昂的分解操作。另一个问题是目前的方法都是逐层执行低秩近似,无法执行全局参数压缩,因为不同的层具备不同的信息。最后,分解需要大量的重新训练来达到收敛。
3、迁移/压缩卷积滤波器
虽然目前缺乏强有力的理论,但大量的实证证据支持平移不变性和卷积权重共享对于良好预测性能的重要性。
使用迁移卷积层对 CNN 模型进行压缩受到 Cohen 的等变群论(equivariant group theory)的启发。使 x 作为输入,Φ(·) 作为网络或层,T(·) 作为变换矩阵。则等变概念可以定义为:
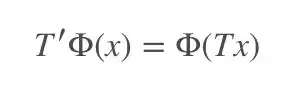
即使用变换矩阵 T(·) 转换输入 x,然后将其传送至网络或层 Φ(·),其结果和先将 x 映射到网络再变换映射后的表征结果一致。注意 T 和 T' 在作用到不同对象时可能会有不同的操作。根据这个理论,将变换应用到层次或滤波器 Φ(·) 来压缩整个网络模型是合理的。
使用紧凑的卷积滤波器可以直接降低计算成本。在 Inception 结构中使用了将 3×3 卷积分解成两个 1×1 的卷积;SqueezeNet 提出用 1×1 卷积来代替 3×3 卷积,与AlexNet 相比,SqueezeNet 创建了一个紧凑的神经网络,参数少了 50 倍,准确度相当。
这种方法仍有一些小问题解决。首先,这些方法擅长处理广泛/平坦的体系结构(如 VGGNet)网络,而不是狭窄的/特殊的(如 GoogleNet,ResidualNet)。其次,转移的假设有时过于强大,不足以指导算法,导致某些数据集的结果不稳定。
4、知识蒸馏
利用知识转移(knowledge transfer)来压缩模型最早是由 Caruana 等人提出的。他们训练了带有伪数据标记的强分类器的压缩/集成模型,并复制了原始大型网络的输出,但是,这项工作仅限于浅模型。
后来改进为知识蒸馏,将深度和宽度的网络压缩成较浅的网络,其中压缩模型模拟复杂模型所学习的功能,主要思想是通过学习通过 softmax 获得的类分布输出,将知识从一个大的模型转移到一个小的模型。
Hinton 的工作引入了知识蒸馏压缩框架,即通过遵循“学生-教师”的范式减少深度网络的训练量,这种“学生-教师”的范式,即通过软化“教师”的输出而惩罚“学生”。为了完成这一点,学生学要训练以预测教师的输出,即真实的分类标签。这种方法十分简单,但它同样在各种图像分类任务中表现出较好的结果。
基于知识蒸馏的方法能令更深的模型变得更加浅而显著地降低计算成本。但是也有一些缺点,例如只能用于具有 Softmax 损失函数分类任务,这阻碍了其应用。另一个缺点是模型的假设有时太严格,其性能有时比不上其它方法。