最近浅学了一下匈牙利算法,略有感触,发文记录一下
匈牙利算法是用在二分图匹配中的
所以要先知道二分图的几个概念
二分图:
有这么一个图
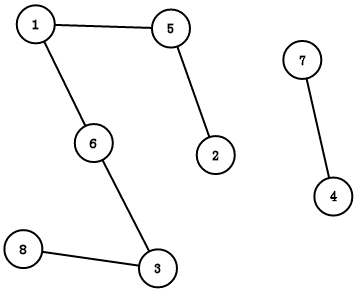
把一个图的顶点划分为两个不相交的集合 U 和 V ,且使得每一条边都分别连接 U 、V 中的顶点,如果存在这样的划分,则称此图为二分图。
简单说,就是可以把一个图分为两部分,同一部分里没有边相连
如图:
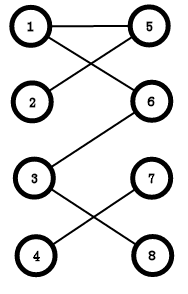
匹配:
二分图匹配就是边集中的任意两条边没有公共顶点
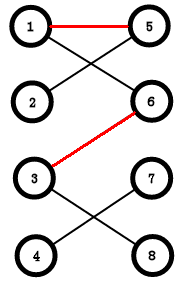
如图,图中的红边叫做匹配
最大匹配:
一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配
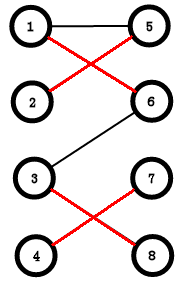
当然,最大匹配不一定只存在一种
完美匹配
如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配
上图就是一个完美匹配,完美匹配一定是最大匹配,完美匹配也可能存在多种,但并不是所有的图都有完美匹配
然后开始我们的匈牙利算法
接着是关于它的两个概念
交替路
从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边······形成的路径叫交替路。
增广路:
从一个未匹配的点出发,走交替路,如果路过一个未匹配的点(第一个点除外),这条交替路叫增广路
匈牙利算法的核心是:不断寻找增广路,并扩展增广路。不断重复这一过程直到找不到增广路为止。
如果现在看不懂,可以看完算法流程再后过头来看
请自动将图脑补成从左侧指向右侧的有向图我才不会说是我懒得改了呢
算法流程(深搜):
我们用link[v] = u表示u连向了v,也就是u和v配对
因为我们要从一边找另一边的最大匹配,所以我们要不断清空标记,标记另一侧没有被访问过
从1号点开始搜到5
5没有被标记过,标记一下,发现没有一个和5配对的点,记录一下link[5] = 1。
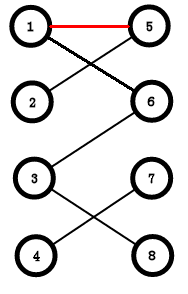
清空标记
接着搜2,找到5,5没有被标记过,打一下标记,记录一下5和2配.......等等,我们发现有5已经和1配对了,那怎么办,我们就搜一下和5配对的1,看1可不可以换一个
那就搜1呗,5被标记过了,然后走到了6,6没被标记过,也没有一个点和6配对,于是link[6] = 1;
这时1和6pd,那么2就可以和5配对;
这时图就变成了这样:
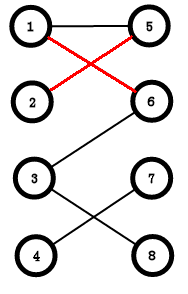
清空一下标记,接着搜下一个点3:
发现3指向了6,6没有被标记,标记一下,发现有一个点6和1配对,我们就搜一下和6配对点1,看1能不能再换个
搜1,找到了5,发现5没被标记过,标记一下,但有一个点2和5配对了,那就搜2
搜2,2连向的点5被标记了,2也没有别的连边,这条路走到头了,没有一个满足条件的点,所以很遗憾,3不能和6配对
接着找3的连边,3还连向8,8没有被标记过,也没有和8配对的,记录一下link[8] = 3
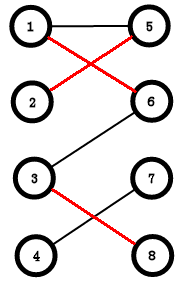
清空标记,搜下一个点4,4连向7,7没有被标记过,7也没有和别的点配对,link[7] = 4;
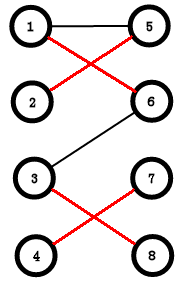
这样我们就走了一遍算法的流程,找到了这个二分图的最大匹配
匈牙利算法实际上就是一个搜索配对的过程
网上说BFS在小规模的数据里跑的比DFS快,但数据较大时两者差不多,但是看到DFS的10行和BFS的n行,果断选择DFS
代码(邻接表):
vis//标记
link//记录配对
head,e//邻接表的操作
a[i][j]//邻接矩阵标记i到j有一条边
bool dfs(int u) {
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!vis[v]) {
vis[v] = 1;
if(link[v] == -1 || dfs(link[v])) {
link[v] = u;
return 1;
}
}
}
return 0;
}
代码(邻接矩阵):
bool dfs(int u) {
for(int v = 1; v <= m; ++ v) {
if (!vis[v] && a[u][v]) {
vis[v] = 1;
if (link[v] == -1 || dfs(link[v])) {
link[v] = u;
return 1;
}
}
}
return 0;
}
查询:
//我们只要搜一侧就可以了
//如果这边的点多,那一定能遍历到另一边的所有点(如果有连边的话)
//如果这边的少,那最大匹配一定<=这边点的个数
memset(link,-1,sizeof(link));
for(int i = 1; i <= n; ++ i) {
memset(vis,0,sizeof(vis));
if(dfs(i)) ans ++;
}
关于匹配的概念就这些,这是在做题过程中可能会遇到的概念
顶点覆盖:
在顶点集合中,选取一部分顶点,这些顶点能够把所有的边都覆盖了。这些点就是顶点覆盖集
最小顶点覆盖:
在所有的顶点覆盖集中,顶点数最小的那个叫最小顶点集合。
独立集:
在所有的顶点中选取一些顶点,这些顶点两两之间没有连线,这些点就叫独立集
最大独立集:
在左右的独立集中,顶点数最多的那个集合
路径覆盖:
在图中找一些路径,这些路径覆盖图中所有的顶点,每个顶点都只与一条路径相关联。
最小路径覆盖:
在所有的路径覆盖中,路径个数最小的就是最小路径覆盖了。
定理:
König定理最大匹配 = 最小顶点覆盖
性质:
最大独立集 = 顶点个数 – 最小顶点覆盖(最大匹配)
最大团 = 补图的最大独立集
最小边覆盖 = 二分图最大独立集 = 顶点个数 - 最小路径覆盖
最小路径覆盖 = 顶点个数 - 最大匹配数
最小顶点覆盖 = 最大匹配数
最小顶点覆盖 + 最大独立数 = 顶点个数
some例题:
HDU 1068 Girls and Boys
HDU 1150 Mac hine Schedule
HDU 1151 Air Raid
HDU 1179 Ollivanders
HDU 1281 棋盘游戏
HDU 1498 50 years, 50 colors
HDU 2119 Matrix
HDU 2063 过山车
HDU 3861 The King’s Problem