0.特殊的矩阵
a.单位矩阵
类似于标量中的数字1,任何矩阵和单位矩阵相乘的结果还是原来的矩阵,。如下是一个三阶的单位矩阵:
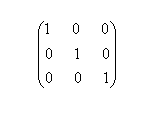
b.转置矩阵
对一个矩阵的行列进行交换,可以得到转置矩阵

c.逆矩阵
对于一个方阵M,它的逆矩阵用M-1来表示,一个重要的性质是:M*M-1=单位矩阵
逆矩阵是具有几何意义的,我们知道一个矩阵可以表示一个变换,而逆矩阵允许我们还原这个变换。因此,如果我们使用变换矩阵M对矢量v进行了一次变换,然后再使用它的逆矩阵M-1进行另一次变换,那么我们会得到原来的矢量
证明为:M-1*(M*v)=(M-1*M)*v=v
d.正交矩阵
矩阵M是正交的,等价于:M*MT=单位矩阵
结合上面的逆矩阵性质,可知对于正交矩阵M:MT=M-1
1.矩阵和矩阵的乘法
一个a*b的矩阵和一个b*c的矩阵相乘,结果为一个a*c的矩阵
2.矩阵和矢量的乘法
在unity中,通常会把矢量放在矩阵的右侧,即把矢量转换成列矩阵来进行运算。这是由unity提供的内置矩阵(如MVP矩阵)决定的,矢量放在左侧还是右侧,结果是不一样的
例如,一个4*4的矩阵,乘以一个4*1的向量,结果为一个4*1的向量
对于CBAv=(C(B(Av))),其中C、B、A为矩阵,v为向量,先对v使用A进行变换,再使用B进行变换,最后使用C进行变换
3.几何意义
a.变换
矩阵的几何意义是变换,变换包含常见的平移变换、旋转变换、缩放变换,分别通过构造平移矩阵、旋转矩阵、缩放矩阵,然后乘以点或矢量,就可以对点或矢量进行对应的操作
如果使用的是4*4的矩阵来进行变换,则需要把点或矢量扩展到四维空间,这就是齐次坐标空间
b.齐次坐标
齐次坐标是一个四维矢量
对于一个点,从三维坐标转为齐次坐标,是把其w分量设为1
对于一个矢量,从三维坐标转为齐次坐标,是把其w分量设为0
这样的话,当用一个4*4的变换矩阵对一个点进行变换时,平移、旋转、缩放都会作用于该点;而如果是用于变换一个矢量,平移的效果就会被忽略
旋转变换和缩放变换的矩阵是3*3的,平移变换的矩阵是4*4,点要考虑平移,而方向矢量不需要考虑平移,因此:
对顶点的的变换,通常使用4*4的变换矩阵
对方向矢量的的变换,通常使用3*3的变换矩阵
4.CG中的矩阵
a.初始化
在CG中,对float4x4等类型的变量是按行优先的方式进行填充的,例如用1到9去填充一个3x3的矩阵,则得到的是:
1 2 3
4 5 6
7 8 9
b.访问
访问一个矩阵中的元素时,也是按行来索引,例如定义上面的矩阵为M,则:
M[1][0]表示访问第2行第1列的元素,即值为4
c.mul方法
如下,M为矩阵,v为矢量,tranpose方法表示对矩阵进行转置。可知当参数位置调转时,要对矩阵进行转置
mul(M, v) == mul(v, tranpose(M))
mul(v, M) == mul(tranpose(M), v)