计算机中数的表示和存储（总结）

一、 无符号数和有符号数

1.无符号数

计算机中的数均存放在寄存器中，通常称寄存器的位数为机器字长。所谓的无符号数即没有符号的数，在寄存器中的每一位均可用来存放数值。而当存放有符号位时，则留出位置存放“符号”。因此，在机器字长相同时，无符号数与有符号数所对应的数值范围是不同的。以机器字长16位为例子，无符号数的范围为0~（2¹⁶-1=65535），而有符号数的表示范围为（-32768=2­­­¹⁵）~（+32767=2¹⁵-1）（此数值对应原码表示）。机器中的有符号数是用补码表示的。

2.有符号数

       对于有符号数而言，符号的正负机器是无法识别的，而在机器中是用0,1分别表示正，负的，并规定将它放在有效数字的前面，这样就组成了有符号数。

       把符号“数字化”的数叫做机器数，而把带“+”或“-”符号的数叫做真值。一旦符号数字化后，符号和真值就形成了一种新的编码。有符号数有原码、补码、反码和移码等四种表示形式。

      2.1 有符号数的编码方法-原码表示法

       原码是机器数中最简单的一种表示形式，其符号位为0表示正数，为1表示负数，数值位即真值的绝对值，故原码又称作带符号位的绝对值表示。

       整数原码的定义为

                           

       式中x为真值，n为整数的位数。例如，当x=-1110时，[x]_原=2⁴-(-1110)=11110

       小数的原码定义为

　　　　　　　　　　                           

       例如，当x=-0.1101时，[x]_原=1-(-0.1101)=1.1101

       当x=0时

              [+0.0000]_原=0.0000

              [-0.0000]_原=1-(0.0000)=1.0000

       可见[+0]_原不等于[-0]_原，即原码中的零有两种表示形式。

       原码编码的优缺点

       其表示简单明了，易于和真值转换，但用原码进行加减运算时，确带来了许多麻烦。

2.2 有符号数的编码方法-补码表示法

补码利用了生活中的“补数”的概念，即以某个数为基准，称为模数，该数对模数的取模运算的结果就是补数。例如，-3=+9（mod12），4=4（mod12）=16（mod12）。

所以，一个负数可用它的正补数来代替，而这个正补数可以用模加上负数本身求得。这样减法可以用加法替代。

整数补码的定义为

　　　　　　　　　　

式中x为真值，n为整数的位数。例如，当x=-1110时，[x]_原=2⁴⁺¹+(-1110)=10010

小数补码的定义为

                           

例如，当x=-0.1101时，[x]_原=2+(-0.1101)=10.0000-0.1101=1.0011

当x=0时

              [+0.0000]_补=0.0000

              [-0.0000]_补=2+(-0.0000)=10.0000-0.0000=0.0000

       或   [+0]_补=00

              [-0]_补=2_­¹⁺¹+(-0)=100-0=00

       可见[+0]_原=[-0]_原，即原码中的零只有一种表示形式。

       对于x=-1，若将其看成整数，则[-1]_补=2¹⁺¹ +(-1)=100-1=11；若将其看成小数，有[-1]_补=2+(-1)=10.0000-1.0000=1.0000。可见，-1本不属于小数范围，但却有[-1]补存在，故它能比原码多能表示一个“1”。

       原码和补码的转换准则：

       对于负数（整数或小数），无论是原码­→补码还是补码→原码,都遵守“除符号位外，每位取反，末位加1”得到，而原码→补码遵守“符号位不变，每位取反”。

2.3 有符号数的编码方法-反码表示法

       反码通常用来作为由原码求补码或者由补码求原码的中间过渡。反码的定义如下：

整数补码的定义为

                           

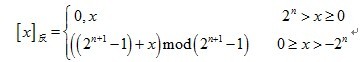
式中x为真值，n为整数的位数。例如，当x=-1110时，[x]_原=(2⁴⁺¹-1)+(-1110)=10001

小数反码的定义为

                           

例如，当x=-0.1101时，[x]_原=(2-2^-4)+(-0.1101)=1.1111-0.1101=1.0010

当x=0时

              [+0.0000]_补=0.0000

              [-0.0000]_补=(10.0000-0.0001)+(-0.0000) = 1.1111

可见[+0]_原不等于[-0]_原，即原码中的零有两种表示形式。

       有[y]_补→[-y]_补，无论真值是正还是负，都是采用“连同符号位在内，每位取反，末位加1”的规则。

2.4 三种编码方式+无符号的表示范围

对于机器字长为n（例如8），无符号数的范围为0~(2ⁿ-1)=255，原码、反码的范围为-(2^n-1-1)=-127~(2^n-1-1)=127，补码范围为-(2^n-1)=-128~(2^n-1-1)=127。考虑一个机器码10000000=0x80，对应无符号数就为128；原码为-0；反码为-127（对应原码为11111111）；补码为-128（由于补码可以表示最小的负数-2ⁿ⁼⁷=-128（真值）即[-128]_补=2⁷⁺¹-1000000=10000000或=2⁸⁺¹-1000000=1 10000000，即看成如果是9位则变成原码为1 10000000，但只有8位所以10000000补码就表示-128，而这个数字在原码和反码中都没法表示）。

2.5 移码

当真值用补码表示时，由于符号位和数值部分一起编码，与习惯上的表示法不同，因此人们很难从补码的形式上直接判断其真值的大小。

如果我们对每个真值加上一个2ⁿ（n为整数的位数），则可以直接比较各数的大小了。

由此可得移码的定义为

                                   [x]­_移=2ⁿ+x  （2ⁿ>x≥-2ⁿ）

式中x为真值，n为整数的位数。从其定义可以看出：移码的首位一样表示符号位，但和上述三种编码不同，其0表示为负数，1表示为整数。

其实移码就是在真值上加上一个常数2ⁿ。在数轴上移码所表示的范围恰好对应于真值在数轴上的范围向轴的正方向移动2ⁿ个单元。由此得移码之称，如下图所示：

 　　　　　　　　　　　　

当x=0时

       [+0]_移=2⁵+0=1,00000

       [-0]_移=2⁵-0=1,00000

可见，[+0]_移=[-0]_移，即移码表示中零也是唯一的。

由移码的定义知，当n=5时，其最小的真值为x=-2⁵=-100000，则[-100000]_移=2⁵+x=0,00000，即最小真值的移码为全0。利用移码这一特点，当浮点数的阶码用移码表示时，就能方便地判断阶码的大小。

进一步观察可以发现，同一个真值的移码和补码仅差一个符号位。

二、 C/C++语言中如何处理

C/C++语言中有unsigned类型、int类型及long int类型对应于整型的表示，计算机存储有符号数都是用补码表示的（实验验证）。win32下的位数分别都为4Bytes，则无符号表示的范围为0~2³²-1=4294967295，int表示的范围为-2³¹~2³¹-1（补码确定的）。

对于1个int类型的数据，当给其赋值时（即我们给的真值），当计算机对其进行存储时，都将该真值编码成了补码的形式，而当以%d形式（带符号的整型）输出时又转变成我们的真值，以x%形式（十六进制无符号整数）输出时则直接输出为补码形式的机器码）。例如：

 int a = -8;

printf("%d,%x\n",a,a);

则输出的结果为-8,fffffff8。

当输入的数越界时（比如说给int赋值超过2³¹-1=2147483647或者-2³¹），则同样将该该数转变成补码形式，然后截断超过的位数。例如：

int a = 2147483649;

printf("%d,%x\n",a,a);

将a表示成机器码为ff ff ff ff + 2 = 80 00 00 01（最高位进位直接去掉），而该补码形式对应的原码为ff ff ff ff，故对应输出的真值为-(2³¹-1)；当输入为2³¹=2147483648时，输出为-2³¹，当超过负数的界时，输出一直未-2³¹。

另外，无符号整数unsigned int中最高位不表示符号位，故当给无符号整数类型的变量赋值一个负数时，计算机存储时将其存为对应的补码形式，而输出的时候则不将首位1看成符号位。例如：

unsigned m5 = -8;

printf("%d,%u,%x,%d\n",m5,m5,m5);

则输出为-8,4294967288,fffffff8.同样，对无符号的输出超过上界时，其输出一直为2³²-1.

       C/C++中的各种数据类型可以进行转换，以其输出格式定。记住一点，有符号数在计算机中存储的都是补码形式。而当为无符号数时，在计算机中存储的形式即可以看成无符号数也可以看成有符号数（此时该机器码为有符号数的补码），故其输出的结果由输出的格式决定。当他们以十六进制或八进制输出时，输出的都是机器码，故不管是有符号还是无符号数，当他们的机器码一样时，输出的结果都一样。

 

参考文献：唐朔飞，计算机组成原理