并查集

题目：给定N个人物和M组朋友关系，计算出他们之间形成多少个朋友圈

举个例子，比如现在有5个宠物，分别是小猫1，小猫2，小猫3，小狗1，小狗2。再告诉你小猫1和小狗1是好朋友，小猫2和小狗1是好朋友，小猫3和小狗2是好朋友。这样它们之间就形成了2个朋友圈。如下图：

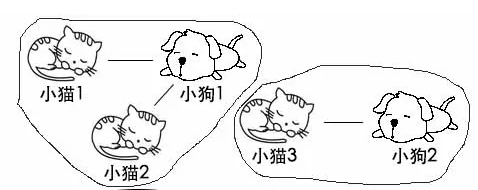
分析：典型的图结构的数据结构，也可用树结构进行处理

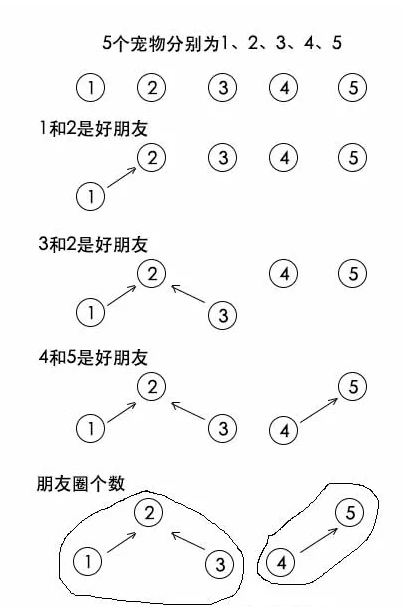
初始时每个节点单独是一棵树，一对好友关系就是把两棵树的树根连接起来

如果1和3是好朋友，并不是连接1和3，而是去找1的根和3的根，发现他们都是2，所以他们本来就在一个朋友圈，不需要相连。

树同样可以用数组存，初始时刻数组中都是-1，当有两个节点需要合并时，只需要将其中一个数的根的值设为另一个数的根的下标就行。

 

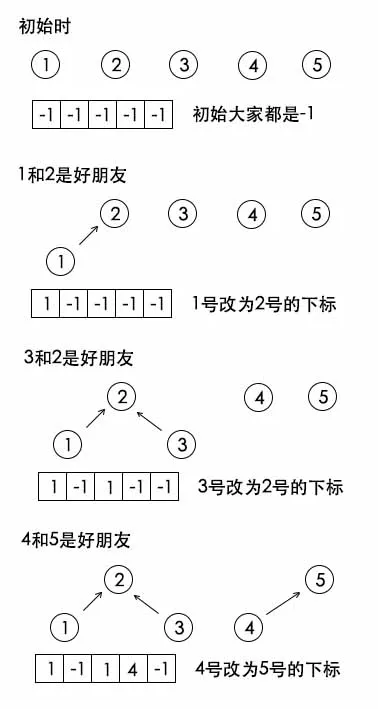
这种结构也叫【并查集】

 JAVA：

import java.io.*;
import java.util.*;

class test  
{
    public static void main (String[] args) throws java.lang.Exception
    {
        UnionFindSet ufs = new UnionFindSet(10);

        ufs.union(0, 1);
        ufs.union(0, 2);
        ufs.union(3, 4);
        ufs.union(3, 1);
        ufs.union(5, 7);
        ufs.union(7, 8);
        ufs.union(7, 8);
        
        ufs.print();
        System.out.println(ufs.count());
    }
    
}
class UnionFindSet {

    // 存储并查集
    private int[] elements;
    // 记录点的使用情况
    private int[] flag;

    UnionFindSet(int n) {
        // 初始都为-1
        elements = new int[n];
        flag = new int[n];
        for (int i = 0; i < n; i++) {
            elements[i] = -1;
            flag[i] = 0;
        }
    }

    // 找到一个数的根
    public int find(int x) {
        while(elements[x] != -1) {
            x = elements[x];
        }
        return x;
    }

    // 把两个数的根连起来
    public void union(int x, int y) {
        flag[x]++;
        flag[y]++;
        // x的根
        int rootx = find(x);
        // y的根
        int rooty = find(y);
        // 如果不是同一个根就连起来
        if(rootx != rooty) {
            elements[rootx] = rooty;
        }
    }

    // 计算形成了多少颗树
    public int count() {
        int count = 0;
        for(int i=0; i<elements.length; i++) {
            if(elements[i] == -1 && flag[i]!=0) {
                count++;
            }
        }
        return count;
    }

    // 打印并查集
    public void print() {
        for(int i=0; i<elements.length; i++) {
            if(flag[i]!=0){
                System.out.print(elements[i] + " ");
            }else{
                System.out.print(" * ");
            }
        }
        System.out.println();
    }

}

输出（* 表示没有形成朋友圈的单独点）：

1 2 -1 4 2 7  * 8 -1  * 
2

优化一：【基于树高度的合并优化】

特殊情况：1和2是好朋友，2和3是好朋友，3和4是好朋友，4和5是好朋友

 

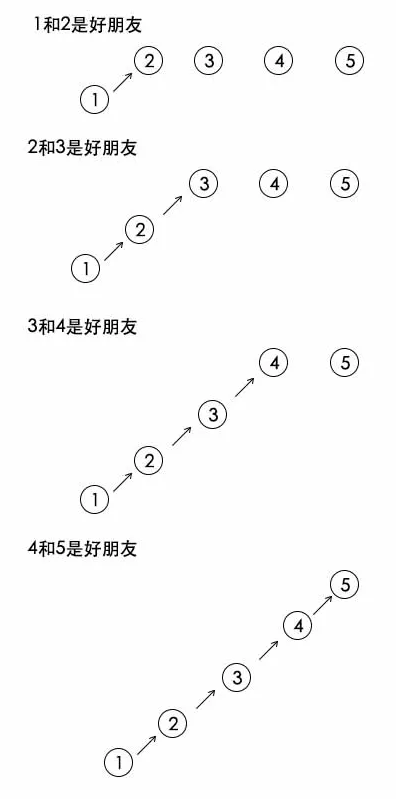
这种情况树就退化成链表，所以树的合并这里可以优化一下，矮的树向高的树合并，尽量避免树的高度无限制的增长

JAVA：

import java.io.*;
import java.util.*;

class test  
{
    public static void main (String[] args) throws java.lang.Exception
    {
        UnionFindSetMergeOptimize ufsmo = new UnionFindSetMergeOptimize(10);

        ufsmo.union(0, 1);
        ufsmo.union(1, 2);
        ufsmo.union(2, 3);
        ufsmo.union(3, 4);
        ufsmo.union(4, 5);
        ufsmo.union(5, 6);
        ufsmo.union(6, 7);
        ufsmo.union(7, 8);
        ufsmo.union(8, 9);

        ufsmo.print();
        System.out.println(ufsmo.count());
    }
    
}
class UnionFindSetMergeOptimize {

    // 存储并查集
    private int[] elements;
    // 存储树的高度
    private int[] heights;
    // 记录点的使用情况
    private int[] flag;

    UnionFindSetMergeOptimize(int n) {
        elements = new int[n];
        heights = new int[n];
        flag = new int[n];
        for (int i = 0; i < n; i++) {
            // 初始都为-1
            elements[i] = -1;
            // 初始高度1
            heights[i] = 1;
            flag[i] = 0;
        }
    }

    // 找到一个数的根
    public int find(int x) {
        while(elements[x] != -1) {
            x = elements[x];
        }
        return x;
    }

    // 把两个数的根连起来
    public void union(int x, int y) {
        flag[x]++;
        flag[y]++;
        // x的根
        int rootx = find(x);
        // y的根
        int rooty = find(y);
        // 如果不是同一个根就连起来
        if(rootx != rooty) {
            // 矮树向高树合并
            if(heights[rootx] > heights[rooty]) {
                elements[rooty] = rootx;
            } else if(heights[rootx] < heights[rooty]) {
                elements[rootx] = rooty;
            } else {
                // 如果高度相同，随便合并
                elements[rootx] = rooty;
                // 但是记得合并后高度加一
                heights[rooty]++;
            }

        }
    }

    // 打印并查集
    public void print() {
        for(int i=0; i<elements.length; i++) {
            if(flag[i]!=0){
                System.out.print(elements[i] + " ");
            }else{
                System.out.print(" * ");
            }
        }
        System.out.println();
        for(int i=0; i<heights.length; i++) {
            System.out.print(heights[i] + " ");
        }
        System.out.println();
    }
    // 计算形成了多少颗树
    public int count() {
        int count = 0;
        for(int i=0; i<elements.length; i++) {
            if(elements[i] == -1 && flag[i]!=0) {
                count++;
            }
        }
        return count;
    }

}

输出：

1 -1 1 1 1 1 1 1 1 1 //树的集合
1 2 1 1 1 1 1 1 1 1  //每个节点的高度
1

 优化二：【路径压缩优化】

每次查找都会顺藤摸瓜的找，直到找到值为-1的根节点为止，与其这样不如直接让这个节点指向根节点。不过这样的话，树的高度会发生变化，基于树的高度优化就会不准了

JAVA：

import java.io.*;
import java.util.*;

class test  
{
    public static void main (String[] args) throws java.lang.Exception
    {
        UnionFindSetPathOptimize ufspo = new UnionFindSetPathOptimize(10);

        ufspo.union(0, 1);
        ufspo.union(1, 2);
        ufspo.union(2, 3);
        ufspo.union(3, 4);
        ufspo.union(4, 5);
        ufspo.union(5, 6);
        ufspo.union(6, 7);
        ufspo.union(7, 8);
        ufspo.union(0, 9);

        ufspo.print();
        System.out.println(ufspo.count());
    }
    
}
class UnionFindSetPathOptimize {

    // 存储并查集
    private int[] elements;
    // 记录点的使用情况
    private int[] flag;

    UnionFindSetPathOptimize(int n) {
        // 初始都为-1
        elements = new int[n];
        flag = new int[n];
        for (int i = 0; i < n; i++) {
            elements[i] = -1;
            flag[i] = 0;
        }
    }

    // 找到一个数的根
    public int find(int x) {
        // 保存原始x值
        int originX = x;
        // 找到根
        while(elements[x] != -1) {
            x = elements[x];
        }
        // 把这一路的节点全部直接连到根上
        while(originX != x) {
            int tempX = originX;
            originX = elements[originX];
            elements[tempX] = x;
        }
        return x;
    }

    // 把两个数的根连起来
    public void union(int x, int y) {
        flag[x]++;
        flag[y]++;
        // x的根
        int rootx = find(x);
        // y的根
        int rooty = find(y);
        // 如果不是同一个根就连起来
        if(rootx != rooty) {
            elements[rootx] = rooty;
        }
    }

    // 计算形成了多少颗树
    public int count() {
        int count = 0;
        for(int i=0; i<elements.length; i++) {
            if(elements[i] == -1 && flag[i]!=0) {
                count++;
            }
        }
        return count;
    }

    // 打印并查集
    public void print() {
        for(int i=0; i<elements.length; i++) {
            if(flag[i]!=0){
                System.out.print(elements[i] + " ");
            }else{
                System.out.print(" * ");
            }
        }
        System.out.println();
    }

}

输出：

8 8 8 8 8 8 8 8 9 -1 
1