ACM FPGA 2019 -- Reconfigurable Convolutional Kernels for Neural Networks on FPGAs 论文解读

Reconfigurable Convolutional Kernels for Neural Networks on FPGAs -2019 ACM FPGA

@(论文笔记)

@

目录

• Reconfigurable Convolutional Kernels for Neural Networks on FPGAs -2019 ACM FPGA
  • 本文的主要贡献：
  • CNN core的设计
    • 1、Generic LUT-based Constant Multiplication （Ken Chapman.‘s Multiplier (KCM))
    • 2、Compressor Trees
    • 3、Run-time Reconfgurable LUTs
    • Generic Architecture
    • Reconfgurable SOP based on CFGLUTs
    • Faithfully Rounded SOP
    • Memory Requirements
    • Online Computation of LUT Contents

reconfgurable constant multipliers (RCMs) showed that

1. RCMs use considerably fewer resources compared to logic-based multipliers and
2. the reconfguration of the coefcients is possible within very few clock cycles
   最新的RCM 使用CFG-LUT, 可以在32个周期内进行重载

本文的主要贡献：

1. 本文设计了一种变体KCM（Ken Chapman.‘s Multiplier / Constant coefficient Multipliers）。使用快速可编程查找表，流水线加法树，faithfor rounding ，以及一种使用CFGLUT的在线可编程电路
2. 本文设计了一种基于FloPoCo代码生成器的自动脚本。
   FloPoCo (Floating-Point Cores) 是一种将算法公式（C,C++）自动转换为VHDL的工具。有点类似HLS.
   http://flopoco.gforge.inria.fr/

CNN core的设计

1、Generic LUT-based Constant Multiplication （Ken Chapman.‘s Multiplier (KCM))

x是原码，等号后面的表示补码到原码的转换。 例如 x=-3，其三位补码表示的x为（101），则有$-3 = -2^2+2^0$。 将x与Cn（$B_c$比特）相乘，可以将乘法分解为若干个小的乘法，每个都是$B_c imes L$。

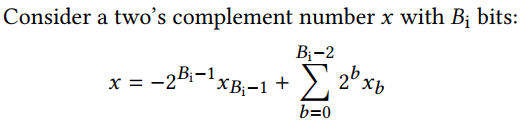
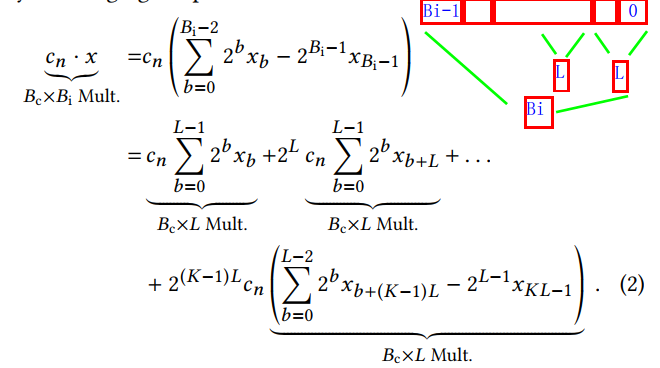
(K = [B_i/L]) 当Bi不能被L整除时，需要将Bi扩展。
所使用的KCM乘法器结构如下：其中，只有第一个计算Bi-1到Bi-L-2部分的乘法器是signed,其余都是unsigned.

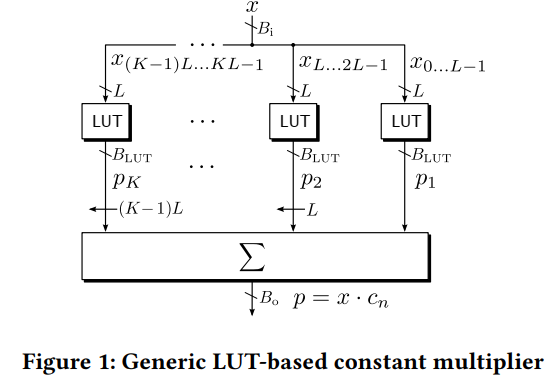
2、Compressor Trees

上图中最后的求和部分可以使用加法树实现。本文指出，传统的加法树是基于全加器和半加器设计的，在FPGA上映射到LUT上是十分低效的。因此本文使用Parandeh-Afshar提出的 generalized parallel counters (GPCs)。

3、Run-time Reconfgurable LUTs

confgurable lookup tables (CFGLUTs) 在现在的Xilinx FPGA中大部分都支持。其内容可以再运行时更改。
在 Reconfigurable LUT: A Double Edged Sword forSecurity-Critical Applications 中有比较详细的说明。

接受5个输入，可以作为5-1查找表配置，也可以作为4-2查找表配置。I4~I0是5个输入，O5,O6是输出。LUT有初始化INIT值，用来表示初始的真值表。该值可以再运行时被用户修改。 当reconfiguration使能信号CE为高时，通过CDI接口接收一个1bit的数据，每过一个周期将该比特数据移位进入32位的INIT寄存器中，同时旧的值从CDO移出。 例如将INIT的内容

需要32个周期完成配置：

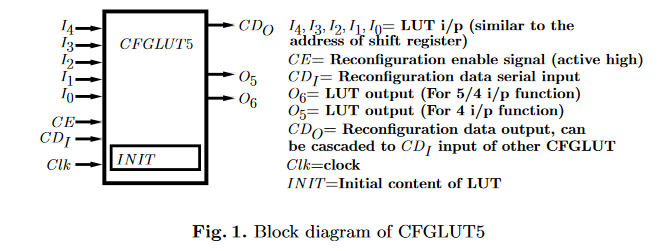
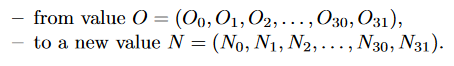
Generic Architecture

上述只是一个乘法的LUT结构，而神经网络需要求多个乘法的和，因此本文的乘加器结构（sum of products (SOP)）如下：

乘法器使用KCM，加法器使用加法树。值得一提的是，此处每个乘法器都是Bi位宽的，并且在内部被细分为K个小乘法器，每个小乘法器的位宽是跟查找表的输入个数有关的。例如使用CFGLUT（5-1或者4-2）则 L=5或4. Lut的输出位宽BLUT = L + Bc，Bc是乘数的位宽。每个lut的输出都会经过一个移位器，表示该部分代表乘法的第几部分。最终的结果位宽为B0, 对于超出该位宽的值会提前进行截断。

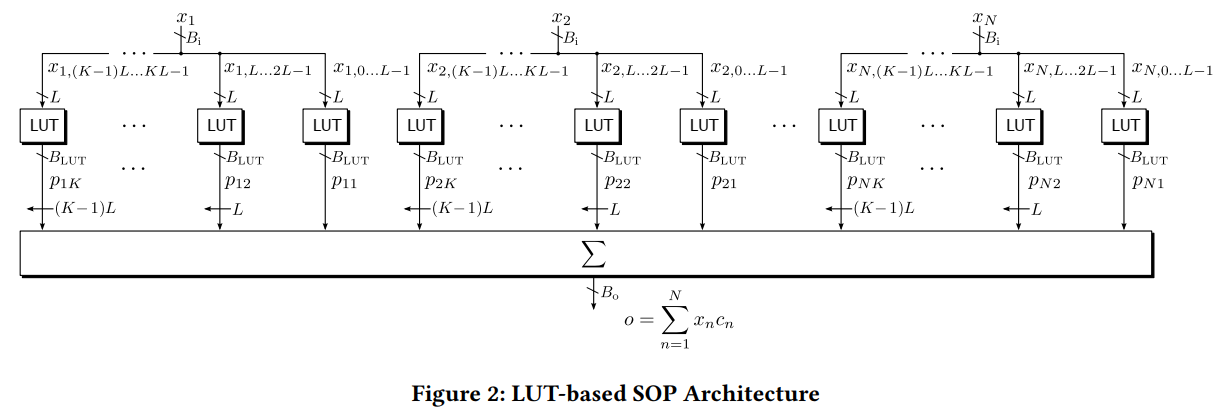
Reconfgurable SOP based on CFGLUTs

本位使用CFGLUTs构建可重构乘法器，使用4输入2输出模式，(I_4)置高，只使用(I_0~I_3)作为输入，(O_5,O_6)作为输出。因此将输入(B_i)位宽的feature分割为L=4的小块，输入查找表。对于一个大小为N的kernel size, 计算N个weight与feature的乘加操作需要消耗的lut个数为

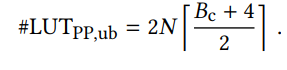
(Bc + 4) 时每个小乘法器的输出位宽，Bc是weight的位宽。由于每个CFGLUT只有两个outputs，因此计算一次4 bit*Bc bit的运算需要(（Bc + 4）/2)个LUT.

Faithfully Rounded SOP

加法树的输出的位宽比输入乘数的位宽要大许多，因此需要对其进行截位。一般来说，截位到q位会引入最大为(2^{-q})的误差。而四舍五入则会引入(2^{-q-1})的误差。对多个数截位再相加，其误差会累加，为了降低截位带来的误差，文中使用了一种Faithful rounding 的方法。可以使得多个截位后的数累加后，其误差仍然能保持或者小于(2^{-q})。主要思想是引入保护位g，使得在截断时截断到q+g位，相当于在求和时多保留几位，这样的截断误差为

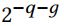
假设K是每个乘法器包含的4位乘法器个数：

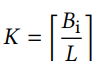
则总的截断误差为：

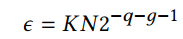
（个数*每个的误差）
要使最后的误差小于(2^{-q})，只要使：

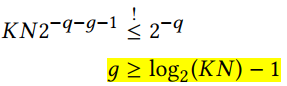
也就是

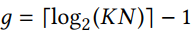
即可 。
所以只要在计算时保留到q+g位，最后round到q位。在q+1位上要做rounding,可以通过在该位加上该位表示的数值的一半，之后截位实现。

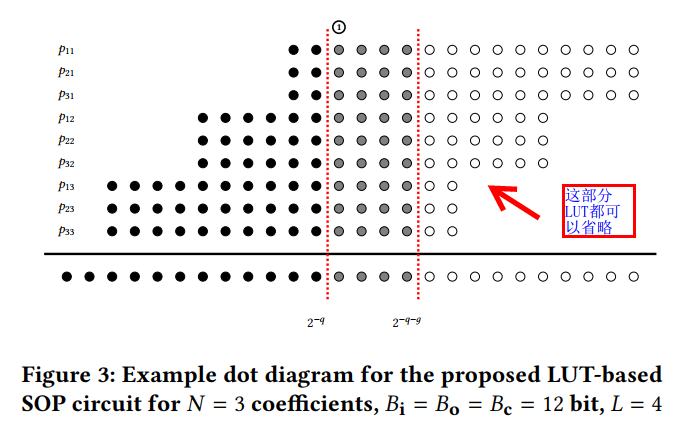
Memory Requirements

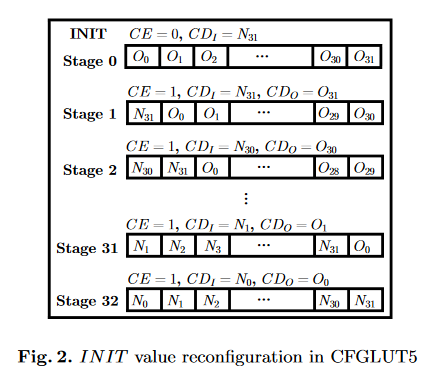
上述方法带来的问题是，LUT计算需要大量的memory（每个需要32bit）的INIT buffer，导致实际存储量是kernel size的32倍 左右。因此需要使用online confguration。

Online Computation of LUT Contents

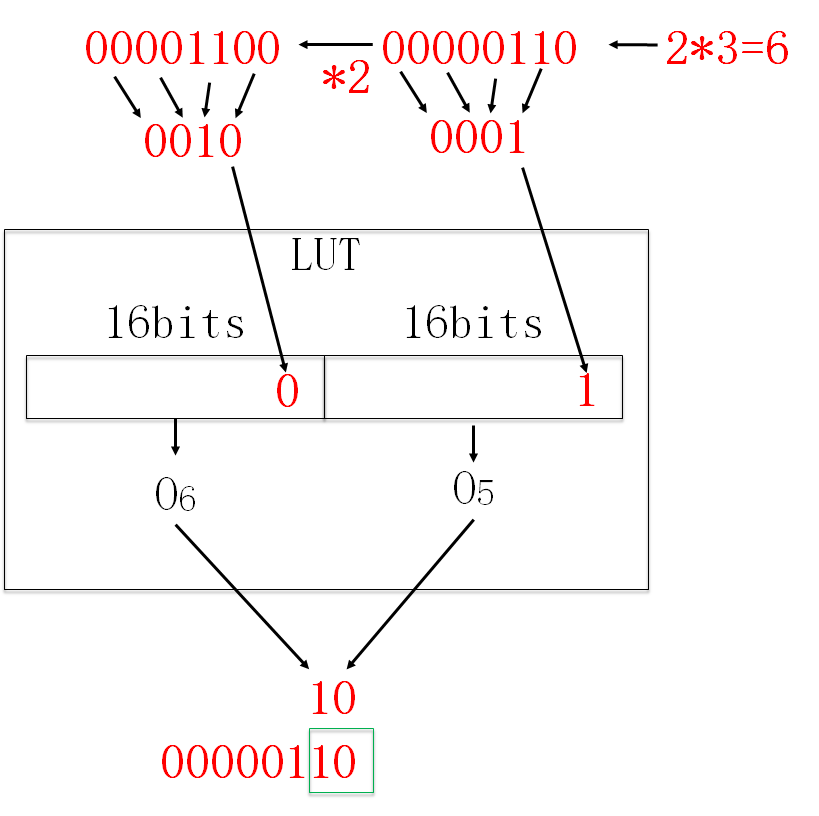
每个LUT配置为4-2的模式，输出两个比特的partial product. 两个比特的高位输出乘法结果的偶数位，低位输出奇数位。例如下图中O6输出的是乘法结果的第0，2，4... 位。而O5输出的是第1，3，5...位。

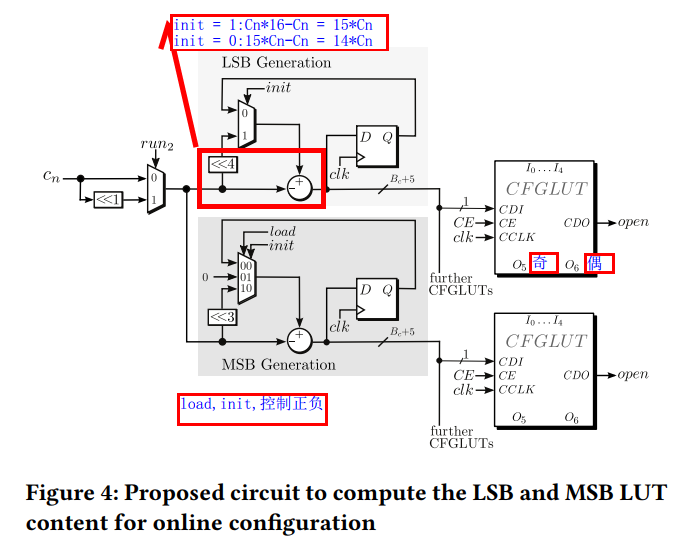
配置电路要配置（遍历4比特数与weight Cn的乘积）16*2个周期才能将一个weight与输入的所有可能结果存完。这里*2是因为CDI每次只接收一个比特的输入，而配置LUT内部存储内容时，首先存的是奇数位的16个可能的结果，用O5来输出该部分结果。之后存16个偶数位的可能结果，用O6输出。
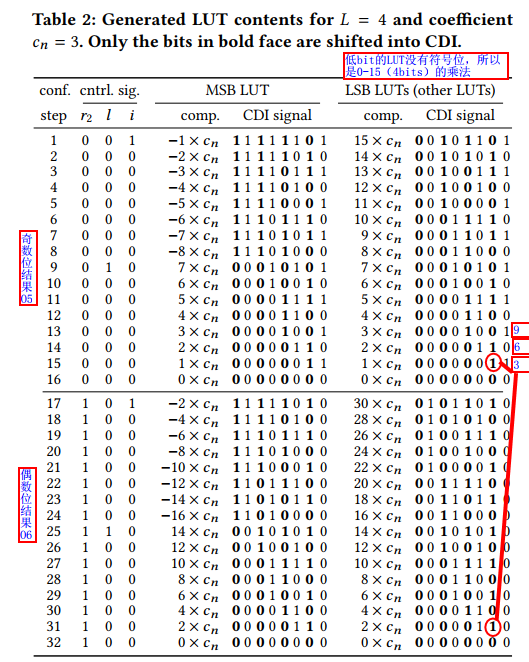
首先来看配置电路的原理。配置电路的目的是在32个周期内生成两bit的所有结果，对于LSB，也就是输入Xn的低位（0~L-1; L~L+3...）是没有符号位的，所以输入范围是0-15. init信号拉高时，CDI的结果是15*Cn, 之后每过一个周期减去一个CDI。如此16个周期算出来了所有可能的结果。对于MSB，事实上只有最高位的LUT需要该电路（Bi-L-4 ~Bi-1）。因此需要负数，用load和init控制，原理与LSB类似。
例如下图的例子：当weight （Cn）时3时， 配置电路首先遍历Cn*4bit数的所有可能结果，如LSB LUT列中 CDI signal的值，表示了乘积的所有结果。而图中说每个CDI只接受加粗部分的输入，也就是乘法结果的偶数位，是因为奇数位和偶数位的关系。例如当输入的4bit数=2时，结果应该时2*3=6
二进制结果00000110，此时O5输出第1位=1，O6输出第0位=0. 所以文中说先算奇数位，也就是将00000110取0，2，4，6位上的数0001.再将Cn*2,相当于把乘法结果往左边移动一位，再取0，2，4，6位的数：0010. 这样O5O6组合出来的乘积结果就是10，表示的是2*3的结果6：00000110的低2bit。