10.24testT3

序列
seq.cpp/in/out
1s / 32M
【题目描述】
山山有一个长度为 N 的序列 A,现在他想构造一个新的长度为 N 的序列
B,使得 B 中的任意两个数都互质。
并且他要使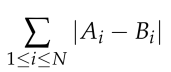

请输出最小值。
最小。
【输入格式】
第一行包含一个数 N 代表序列初始长度
接下来一行包含 N 个数 A1 , A2 ,..., AN ,代表序列 A
【输出格式】
输出包含一行,代表最小值
【样例输入】
5
1 6 4 2 8
【样例输出】
3
【样例说明】
样例中 B 数组可以为 1 5 3 1 8
【数据范围】
对于 40% 的数据,1 ≤ N ≤ 10
对于 100% 的数据,1 ≤ N ≤ 100,1 ≤ ai ≤ 30

分析：最开始拿到这个题，我采取了暴搜+剪枝的策略。然而时间复杂度太高，只拿了部分分。

首先题目要求你构造一个序列，使所有元素互质，从此我们可以提取出一个性质：所有元素的素数因子都不相同。

题目又要求，构造出的序列与原序列的差值的绝对值之和最小。而对于两个已知序列的排列，当且仅当两序列rank一一对应时满足。将原数组从大到小排序后，构造出的数组也一定是不降的。

考虑到ai最多变成58，如果变成更大的数还不如变成1，而且58之内只有16个素数 并且可以证明对于两个数a > b，变成的数A >= B

所以最多只有16个最大的数变成素数，其他的数都会变成1。

所以直接对于前16个数dp，dp[i][j]代表到第i个数，状压哪些素因子被用过了，花费最少为多少。枚举一个数来转移即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n,tim,f[20][1<<17],ans=0x3f3f3f3f,a[110],x[20],p[20],yz[70];
bool vis[70];
bool cmp(const int &a,const int &b)
{
    return a>b;
}
void kk()
{
    int t=sqrt(60);
    for(int i=2;i<=t;i++)
    if(!vis[i]){
        for(int j=i*i;j<=60;j+=i)
        vis[j]=1;
    }
    for(int i=2;i<=60;i++)
    if(!vis[i])x[++tim]=i;
}
int main()
{
    scanf("%d",&n);
    p[0]=1;
    for(int i=1;i<=20;i++)p[i]=p[i-1]<<1;
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    sort(a+1,a+1+n,cmp);
    kk();
    for(int i=2;i<=58;i++)
    {
    for(int j=1;j<=tim;j++)
        if(i%x[j]==0)
        yz[i]|=p[j-1];
    }
    int nn=min(n,16);
    memset(f,0x3f3f3f3f,sizeof(f));
    f[0][0]=0;
    for(int i=1;i<=nn;i++)//枚举已经处理到第几项了
    for(int j=0;j<=p[16]-1;j++)//前i项包含的素数因子的状态
        if(f[i-1][j]<0x3f3f3f3f)
        {
        f[i][j]=min(f[i][j],f[i-1][j]+abs(a[i]-1));
        for(int k=2;k<=58;k++)//枚举下一项的取值
            if((j&yz[k])==0)
            f[i][j|yz[k]]=min(f[i][j|yz[k]],f[i-1][j]+abs(a[i]-k));
        }
    for(int i=0;i<=p[16]-1;i++)ans=min(ans,f[nn][i]);
    for(int i=nn+1;i<=n;i++)ans+=abs(a[i]-1);
    printf("%d\n",ans);
    return 0;
}