随着互联网的发展，文本分析越来越受到重视。由于文本格式的复杂性，人们往往很难直接利用文本进行分析。因此一些将文本数值化的方法就出现了。LDA就是其中一种很NB的方法。 LDA有着很完美的理论支撑，而且有着维度小等一系列优点。本文对LDA算法进行介绍，欢迎批评指正。
本文目录：
1、Gamma函数
2、Dirichlet分布
3、LDA文本建模
4、吉普斯抽样概率公式推导
5、使用LDA
1、Gamma函数
T(x)= ∫ tx-1 e-tdt T(x+1) = xT(x)
若x为整数，则有 T(n) = (n-1)!
2、Dirichlet分布
这里抛出两个问题：
问题1： (1) X1, X2......Xn 服从Uniform(0,1)
(2) 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(3) 问X(k1)和X(k1+k2)的联合分布式什么
把整个概率区间分成[0,X1) , [X1, X1+Δ), [X1+Δ, X1+X2), [X1+X2, X1+X2+Δ), [X1+X2+Δ,1]
X(k1) 在区间[X1, X1+Δ), X(k1+k2) 在区间[X1+X2, X1+X2+Δ)。 我们另X3 = 1-X1-X2.
则，
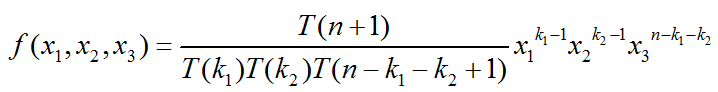
即Dir(x1, x2, x3| k1, k2, n-k1-k2+1)
问题2： (1) X1, X2......Xn 服从Uniform(0,1), 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(2) 令p1 = [0, X(k1)], p2 = [X(k1), X(k1+k2)], p3 = 1-p1-p2
(3) 另外给出新的信息， Y1, Y2.....Ym服从Uniform(0, 1), Yi落到[0,X(k1)], [X(k1), X(k1+k2)], [X(k1+k2), 1]的数目分别是m1, m2, m3
(4) 问后验概率 p(p1,p2,p3|Y1,Y2,....Ym)的分布。
其实这个问题和问题1很像，只是在同样的范围内多了一些点而已。 因此这个概率分布为 Dir(x1,x2,x3| k1+m1, k2+m2, n-k1-k2+1+m3)。
我们发现这么一个规律 Dir(p|k) + multCount(m) = Dir(p|k+m)。 即狄利克雷分布是多项分布的共轭分布。
狄利克雷分布有这么一个性质：如果
则，
3、 LDA文本建模
首先我们想一篇文章是如何形成的：作者在写一篇文章的时候首先会想这个文章需要包含什么主题呢。比如在写武侠小说的时候，首先会想小说里边需要包含武侠、爱情、亲情、搞笑四个主题。并且给这四个主题分配一定的比例（如武侠0.4，爱情0.3，亲情0.2，搞笑0.1）。每个主题会包含一些word，不同word的概率也是不一样的。 因此我们上帝在生成一篇文章的时候流程是这个样子的：
（1）上帝有两个坛子的骰子，第一个坛子装的是doc-topic骰子，第二个坛子装的是topic-wod骰子。
（2）上帝随机的从二个坛子中独立抽取了k个topic-doc骰子，编号1-K。
（3）每次生成一篇新的文档前，上帝先从第一个坛子中随机抽取一个doc-topic骰子，然后重复如下过程生成文档中的词。
<1>、投掷这个doc-topic骰子，得到一个topic的编号z。
<2>、选择K个topic-word骰子中编号为z的的那个，投掷这个骰子， 于是就得到了这个词。
假设语料库中有M篇文章， 所有的word和对应的topic如下表示：
我们可以用下图来解释这个过程:
一共两个物理过程：
第一个过程: 
，这个过程分两个阶段。第一个阶段是上帝在生成一篇文档之前，先抽出一个主题分布的骰子
，这个分布选择了狄利克雷分布（狄利克雷分布是多项分布的共轭分布）。 第二个阶段根据
来抽样得到每个单词的topic。这是一个多项分布。 整个过程是符合狄利克雷分布的。
第二个过程:
,这个过程也分两个阶段。第一个阶段是对每个主题，生成word对应的概率，即选取的骰子
，这个分布也是选择了狄利克雷分布。 第二个阶段是根据
，对于确定的主题选择对应的word,这是一个多项分布。因此，整个过程是狄利克雷分布。
4、吉普斯抽样概率公式推导
LDA的全概率公式为: 
。 由于
是观测到的已知数据，只有
是隐含的变量，所以我们需要关注的分布为：
。 我们利用Gibbs Sampling进行抽样。 我们要求的某个位置i(m,n)对应的条件分布为 
。
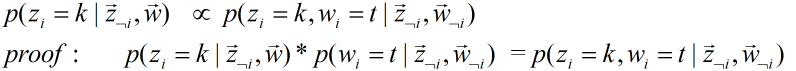
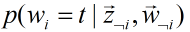是一个定值，因此原公式成立。
下边是公式
的推导:
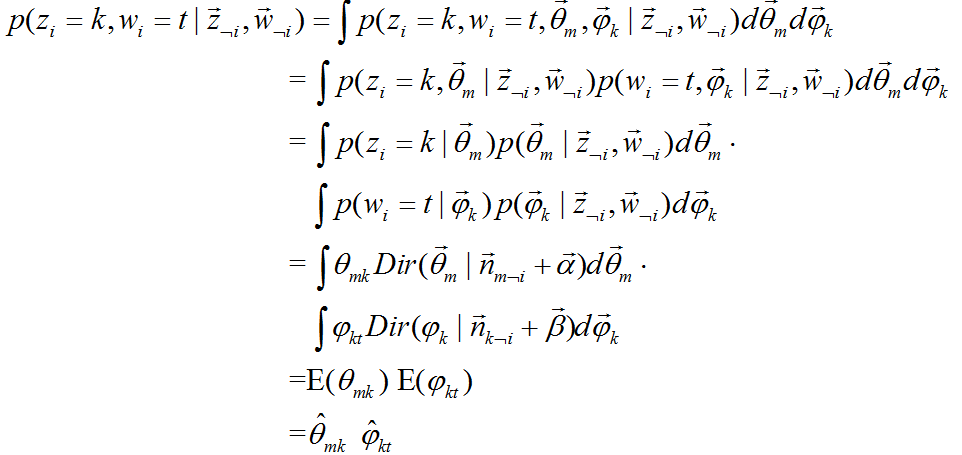
又由于根据狄利克雷分布的特性：
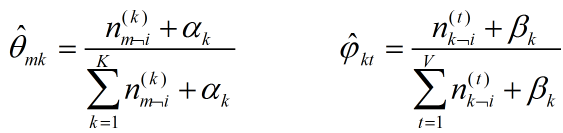
抽样的时候，首先随机给每个单词一个主题，然后用
和
进行Gibbs抽样，抽样后更新这两个值，一直迭代到收敛（EM过程）。
至此抽样就结束了。
5、使用LDA
抽样结束后，我们可以统计和来得到
和
。
对于LDA我们的目标有两个：
(1)得到文章库中每篇文章的主题分布
(2)对于一篇新来的文章，能得到它的主题分布。
第一个目标很容易就能达到。下面主要介绍如果计算 一篇新文章的主题分布。这里我们假设是不会变化的。因此对于一篇新文章到来之后，我们直接用Gibbs Sampling得到新文章的就好了。 具体抽样过程同上。
由于工程上对于计算新的文章没有作用，因此往往只会保存。