Georgia and Bob
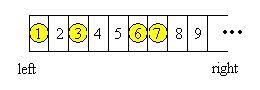
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.
Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.
Given the initial positions of the n chessmen, can you predict who will finally win the game?
一个棋子每一次向左移的最大步数是固定的,而且随着移动减少,不是和取石子很像么?那么和取石子的区别在哪呢?就在于每一次移动时都会让右边相邻的那颗棋子移动空间变大,这样就和取石子只减不增有所不同了,我们应该怎样解决这个问题呢?
我们并不放弃将其与我们熟悉的取石子对应,但我们将策略做小小的变动:
将棋子从右端向左端每相邻两个分为一对,如果只剩一个就将棋盘左端加一格放一颗棋子与之配对,这样配对后好像和以前没有什么区别,但决策时就方便多了,因为我们大可不必关心组与组之间的距离,当对手移动一组中靠左边的棋子时,我们只需将靠右的那一颗移动相同步数即可!同时我们把每一组两颗棋子的距离视作一堆石子,在对手移动两颗棋子中靠右的那一颗时,我们就和他玩取石子游戏,这样就把本题与取石子对应上了。
简单说:/*由于任何两个相邻的棋子只与他们之间的空位有关,所以可以转化为普通的Nim游戏:我们可以把这些空位看作是石子数,谁取得了最后一个空位,谁就是赢家。*/
代码:
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int a[1001],i,t,n,sg;
scanf("%d",&t);
while(t--)
{
sg=0;
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d",&a[i]);
if(n%2!=0)
a[n++]=0;
sort(a,a+n);
for(i=0;i<n;i+=2)
sg^=a[i+1]-a[i]-1;
if(sg==0)
printf("Bob will win
");
else
printf("Georgia will win
");
}
}