K近邻

K近邻

算法思想
一个样本与数据集中的k个样本最相似， 如果这k个样本中的大多数属于某一个类别， 则该样本也属于这个类别。
K值减小就意味着整体模型变复杂，分的不清楚，就容易发生过拟合。

流程：
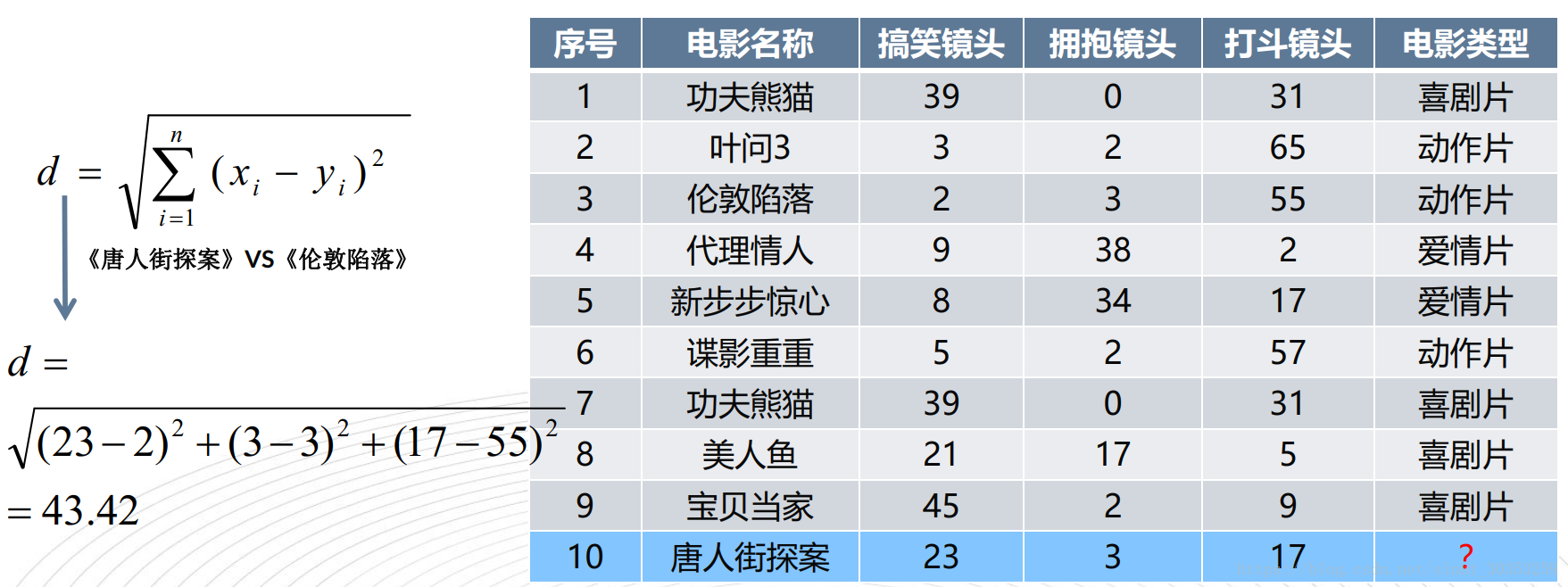
1） 计算已知类别数据集中的点与当前点之间的距离
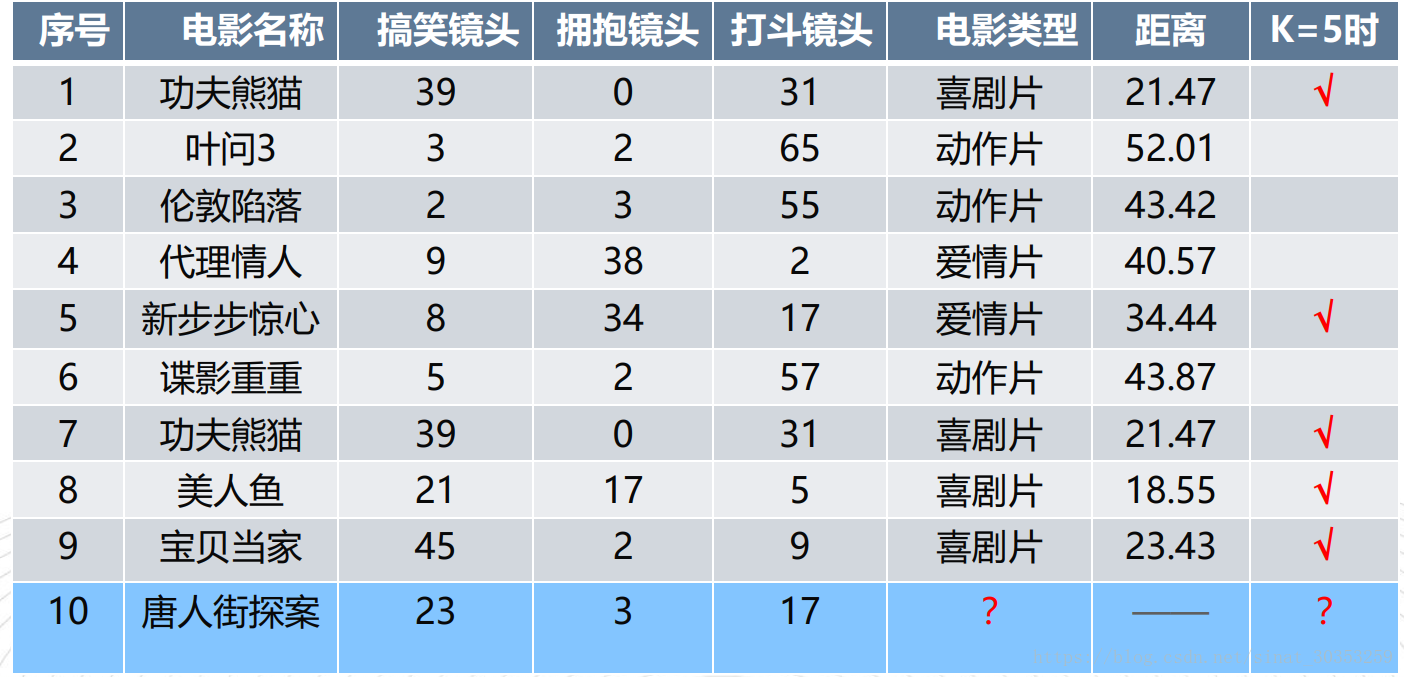
2） 按距离递增次序排序
3） 选取与当前点距离最小的k个点
4） 统计前k个点所在的类别出现的频率
5） 返回前k个点出现频率最高的类别作为当前点的预测分类

优点：

1. 简单有效
2. 重新训练代价低
3. 算法复杂度低
4. 适合类域交叉样本
5. 适用大样本自动分类

缺点：

1. 惰性学习
2. 类别分类不标准化
3. 输出可解释性不强
4. 不均衡性
5. 计算量较大

适用场景：

通常最近邻分类器使用于特征与目标类之间的关系为比较复杂的数字类型，或者说二者关系难以理解，但是相似类间特征总是相似。数据要求归一化，统一各个特征的量纲。

例子：

import math

movie_data = {"宝贝当家": [45, 2, 9, "喜剧片"],
              "美人鱼": [21, 17, 5, "喜剧片"],
              "澳门风云3": [54, 9, 11, "喜剧片"],
              "功夫熊猫3": [39, 0, 31, "喜剧片"],
              "谍影重重": [5, 2, 57, "动作片"],
              "叶问3": [3, 2, 65, "动作片"],
              "伦敦陷落": [2, 3, 55, "动作片"],
              "我的特工爷爷": [6, 4, 21, "动作片"],
              "奔爱": [7, 46, 4, "爱情片"],
              "夜孔雀": [9, 39, 8, "爱情片"],
              "代理情人": [9, 38, 2, "爱情片"],
              "新步步惊心": [8, 34, 17, "爱情片"]}

# 测试样本  唐人街探案": [23, 3, 17, "？片"]
#下面为求与数据集中所有数据的距离代码：
x = [23, 3, 17]
KNN = []
for key, v in movie_data.items():
    d = math.sqrt((x[0] - v[0]) ** 2 + (x[1] - v[1]) ** 2 + (x[2] - v[2]) ** 2)
    KNN.append([key, round(d, 2)])

# 输出所用电影到 唐人街探案的距离
print(KNN)

#按照距离大小进行递增排序
KNN.sort(key=lambda dis: dis[1])

#选取距离最小的k个样本，这里取k=5；
KNN=KNN[:5]
print(KNN)

#确定前k个样本所在类别出现的频率，并输出出现频率最高的类别
labels = {"喜剧片":0,"动作片":0,"爱情片":0}
for s in KNN:
    label = movie_data[s[0]]
    labels[label[3]] += 1
labels =sorted(labels.items(),key=lambda l: l[1],reverse=True)
print(labels,labels[0][0],sep='
')