一、选择题目
因为题目一的分数比题目二高,所以本次选择题目一
题目(1):最大连续子数组和(最大子段和)
背景:给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],...a[n],求该序列如a[i]+a[i+1]+...+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为:Max{0,a[i]+a[i+1]+...+a[j]},1<=i<=j<=n。例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
--引用自《[百度百科]https://baike.baidu.com/item/》
二、单元测试
1、判定条件覆盖法
判定条件覆盖是设计足够的测试用例,得使判断中每个条件的所有可能取值至少执行一次,同时每个判断本身所有可能结果也至少执行一次。缺点是忽略了条件的组合情况。
例如:一个判定包括两个条件如下:y>1andz=0
一组符合判定/条件覆盖的用例需要满足下面
1.使得判定为真
2.使得判定为假
3.使得y>1
4.使得y<=1
5.使得z=0
6.使得z!=0
--引用自《[百度百科]https://baike.so.com/doc/2337618-2472285.html》
2、程序
老师所给题目的第五个程序,所谓的暴力解法
···
include
using namespace std;
int AllSum(int n,int b[])
{
int thissum = 0, sum = 0;
for(int i=0;i<n;i++)
{
thissum=0;
for(int j=i;j<n;j++)
{
thissum+=b[j];
if(thissum>sum)
{
sum=thissum;
}
}
}
if(sum<0)
{
sum=0;
}
return sum;
}
int main()
{
int n,sum=0;
int b[100];
int AllSum(int n,int b[]);
cout<<"输入个数:"<<endl;
cin>>n;
cout<<"输入数组值:"<<endl;
for(int i=0;i<n;i++)
{
cin >> b[i];
}
sum=AllSum(n,b);
cout<<sum<<endl;
system("pause");
return 0;
}
···
相比于暴力解法每一次都从i到j地重新计算一次,这种算法每一次只需要在原来计算的基础上面加上一个数,所以这种算法少了一层循环,时间复杂度为O(n2)是一种比暴力解法要高效的解法
3、测试程序
下面是3个测试的
···
include "stdafx.h"
include "CppUnitTest.h"
using namespace Microsoft::VisualStudio::CppUnitTestFramework;
int thissum = 0, sum = 0;
int AllSum(int n, int b[])
{
for (int i = 0; i<n; i++)
{
thissum = 0;
for (int j = i; j<n; j++)
{
thissum += b[j];
if (thissum>sum)
{
sum = thissum;
}
}
}
if (sum<0)
{
sum = 0;
}
return sum;
}
namespace UnitTest1
{
TEST_CLASS(UnitTest1)
{
public:
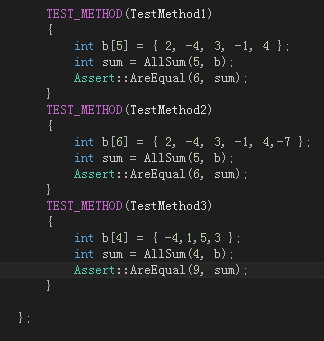
TEST_METHOD(TestMethod1)
{
int b[5] = { 2, -4, 3, -1, 4 };
int sum = AllSum(5, b);
Assert::AreEqual(6, sum);
}
TEST_METHOD(TestMethod2)
{
int b[6] = { 2, -4, 3, -1, 4,-7 };
int sum = AllSum(5, b);
Assert::AreEqual(6, sum);
}
TEST_METHOD(TestMethod3)
{
int b[4] = { -4,1,5,3 };
int sum = AllSum(4, b);
Assert::AreEqual(9, sum);
}
};
}
···
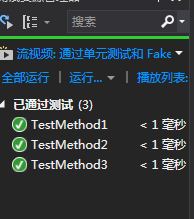
3、结论
过程依旧很坎坷,自己很菜,每次作业都是很艰辛,动手能力有加强,比在其他课学的多
