5 最长公共子串
给定两个字符串a、b,现有k次机会对字符串中的字符进行修改,使修改后两个字符串的最长公共子串最长。每一次修改,可以选择a、b字符串中某一个串的任意位置修改成任意字符。
输入格式
第一行包括一个正整数 k。
第二行和第三行分别输入字符串a、b。(每个串的长度不超过500)
输出格式
输出为一个整数,表示修改后的两个串的最长公共子串长度。
输入样例
5
aaaaa
bbbbb
输出样例
5
Accepted
找两个字符串的最长公共子串,这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
int calculate(string a,string b,int k){ //计算字符串开头开始最长的公共子串
int pos=0; //已访问位置
int K=0;//差异
while(pos<a.size()&&pos<b.size()&&(a[pos]==b[pos]||K<k)){
if(a[pos]!=b[pos]) K++;
pos++;
}
return pos;
}
int main(){
int k;
int lena,lenb;
int max=0;
int i,j;
int ans=0;
string a,b;
cin >>k;
cin >> a >> b;
lena=(int)a.size();
lenb=(int)b.size();
for(i=0;i<lena;i++){
for(j=0;j<lenb;j++){
max=calculate(a.substr(i),b.substr(j),k); //substr :主要功能是复制子字符串,要求从指定位置开始,并具有指定的长度。
if(ans<max) ans=max;
}
}
cout << ans << endl;
return 0;
}
6 旋转骰子
玛莎有n个骰子,每个骰子的6个面上都恰好有一个0到9之间的数字,且同一个骰子6个面上的数字不会重复。
现在玛莎将利用这n个筛子来制作新数字。她把n个骰子摆成一排,然后从左到右查看骰子的上表面并读取,即可得到一个新数字。随后她不断的旋转每个骰子的面就可以得到不同的新数字。旋转骰子需要满足以下规则: 1、制作的数字不能包含前导零; 2、制作新数字时不需要使用所有的骰子; 3、使用骰子旋转,无法将数字9转换为数字6,反之亦然。
给定n个骰子,玛莎可以用它们构成从1到x的所有整数。玛莎想知道,对于给定的n个骰子,这个x的最大取值是多少呢?
输入格式
第一行仅一个整数n,表示骰子的数量(1≤n≤3)。
接下来n行,每行包含6个整数a[i][j](0≤a[i][j]≤9),表示第i个骰子的第j个面上的数字。
输出格式
输出一个整数,即最大数x,玛莎可以使用她的骰子构成数字从1到x。如果无法构成1,则输出0。
输入样例
3
0 1 3 5 6 8
1 2 4 5 7 8
2 3 4 6 7 9
输出样例
98
Accepted
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
int main(){
int n;
int i,j,k,t;
int a[500][500];
cin >> n;
for(i=1;i<=n;i++){
for(j=1;j<=6;j++)
cin >> a[i][j];
}
//n==1
if(n==1){
for(j=1,k=1;j<=6;j++){
if(a[1][j]==k) k++;
}
k--;
cout << k << endl;
return 0;
}
//n==2
if(n==2){
for(j=1,k=1;j<=6;j++){
for(t=1;t<=6;t++)
if(a[1][t]==k||a[2][t]==k) k++;
}
k--;
if(k<9){cout << k << endl;return 0;}
else{
for(k=10,j=1;j<=35;j++){
for(i=1;i<=6;i++){
for(t=1;t<=6;t++)
if(a[1][i]*10+a[2][t]==k||a[1][i]+a[2][t]*10==k) k++;
}
}
k--;
cout << k << endl;return 0;
}
}
if(n==3){
for(j=1,k=1;j<=6;j++){
for(t=1;t<=6;t++)
if(a[1][t]==k||a[2][t]==k||a[3][t]==k) k++;
}
k--;
if(k<9){cout << k << endl;return 0;}
else{
for(k=10,j=1;j<=35;j++){
for(i=1;i<=6;i++){
for(t=1;t<=6;t++) if(a[1][i]*10+a[2][t]==k||a[1][t]+a[2][i]*10==k||a[1][i]*10+a[3][t]==k||a[1][t]+a[3][i]*10==k||a[2][i]*10+a[3][t]==k||a[2][t]+a[3][i]*10==k) k++;
}
}
k--;
cout << k << endl;return 0;
}
}
return 0;
}
7 均等笔
n个人围成一圈,每人有ai支笔。每人可以向左右相邻的人传递笔,每人每次传递一支笔消耗的能量为1。求使所有人获得均等数量的笔的最小能量。
输入格式
第一行一个整数n ,表示人的个数(30%的数据,n<=1000;100%的数据,n<=1e6)。
接下来n行,每行一个整数 ai。
输出格式
输出一个整数,表示使所有人获得均等笔的最小能量。(答案保证可以用64位有符号整数存储)
输入样例
4
1
2
5
4
输出样例
4
Accepted
参考来源:糖果传递
对于每个人,假设他的笔数要经过两类变化:1、从后一个人拿。2、给前一个人,最终的变化结果是变为aver.
- a[1]-X1+X2=aver X2=X1-(a[1]-aver)
- a[2]-X2+X3=aver X3=X1-(a[2]+a[1]-2*aver)
设c[1]=a[1]-aver c[2]=c[1]+a[2]-aver
则有c[i]=c[i-1]+a[i]-aver
则有问题|X1|+|X2|+……+|Xn|的和最小每个都可以用X1表示为|X1|+|X1-c[1]|+|X1-c[2]|+……+|X1-c[n-1]|
绝对值的含义又可以表示数轴上Xi到Ci的距离,所以问题变成了:给定数轴上的n个点,找出一个到他们的距离之和尽量小的点,而这个点就是这些数中的中位数,
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
int a[1000005]={0},x[1000005]={0};
int main(){
int n;
long long sum=0,num=0;
int i=0,j;
int aver;
cin >> n;
for(i=0;i<n;i++){
cin >> a[i];
sum+=a[i];
}
aver=(int)(sum/n);
for(i=0;i<n;i++){
x[i]=x[i-1]-a[i-1]+aver;
}
sort(x,x+n);
j=n/2;
for(i=0;i<n;i++){
num+=abs(x[j]-x[i]);
}
cout << num << endl;
return 0;
}
附:数学证明
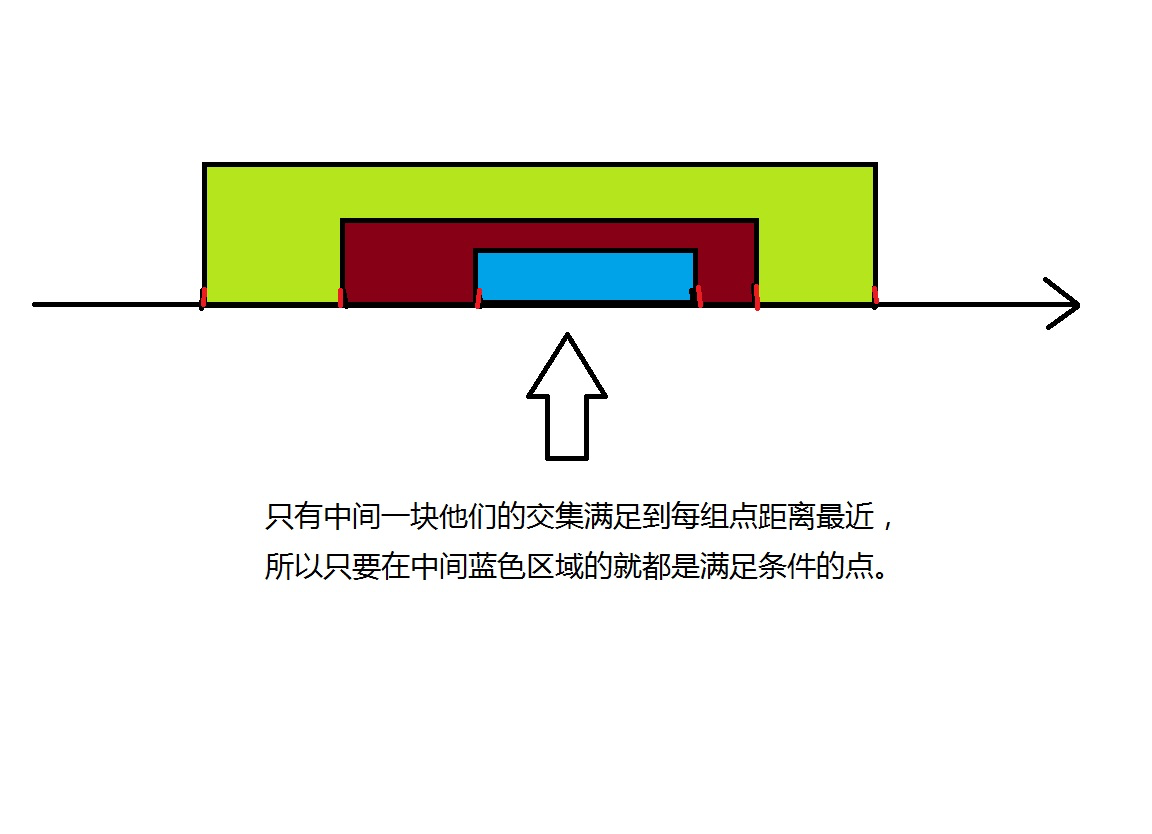
在数轴上有n个点,找出一个点x,使得她到各个点的距离和最小。求证:该点表示的数就是这n个数的中位数。如果我们把数轴上的点两两配对,最大的配最小的,次大的配次小的……则到每组点最近的距离的点在这两个点中间,那么
如果有奇数个点,那么显然中间那个点便为所求。
∴该点表示的数是这n个数的中位数得证。