Lasso回归的坐标下降法推导

 

目标函数

Lasso相当于带有L1正则化项的线性回归。先看下目标函数：RSS(w)+λ∥w∥1=∑Ni=0(yi−∑Dj=0wjhj(xi))2+λ∑Dj=0∣wj∣RSS(w)+λ∥w∥1=∑i=0N(yi−∑j=0Dwjhj(xi))2+λ∑j=0D∣wj∣ RSS(w)+lambda Vert wVert_1=sum_{i=0}^{N}(y_i-sum_{j=0}^D{w_jh_j(x_i)})^2+lambda sum_{j=0}^{D}|w_j| RSS(w)+λ∥w∥1​=∑i=0N​(yi​−∑j=0D​wj​hj​(xi​))2+λ∑j=0D​∣wj​∣
这个问题由于正则化项在零点处不可求导，所以使用非梯度下降法进行求解，如坐标下降法或最小角回归法。

坐标下降法

本文介绍坐标下降法。
坐标下降算法每次选择一个维度进行参数更新，维度的选择可以是随机的或者是按顺序。
当一轮更新结束后，更新步长的最大值少于预设阈值时，终止迭代。

下面分为两部求解

RSS偏导

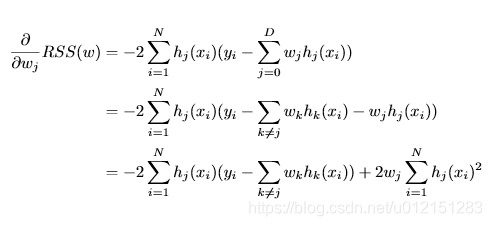
下面做一下标记化简
ρj=∑Ni=1hj(xi)(yi−∑k≠jwkhk(xi))ρj=∑i=1Nhj(xi)(yi−∑k≠jwkhk(xi)) ho_j=sum_{i=1}^Nh_j(x_i)(y_i-sum_{k eq j }w_kh_k(x_i)) ρj​=∑i=1N​hj​(xi​)(yi​−∑k̸​=j​wk​hk​(xi​))
zj=∑Ni=1hj(xi)2zj=∑i=1Nhj(xi)2 z_j=sum_{i=1}^N h_j(x_i)^2 zj​=∑i=1N​hj​(xi​)2
上式化简为∂∂wjRSS(w)=−2ρj+2wjzj∂∂wjRSS(w)=−2ρj+2wjzj frac{partial}{partial w_j}RSS(w)=-2 ho_j+2w_jz_j ∂wj​∂​RSS(w)=−2ρj​+2wj​zj​

正则项偏导

次梯度方法(subgradient method)是传统的梯度下降方法的拓展，用来处理不可导的凸函数。

λ∂wj∣wj∣=⎧⎩⎨⎪⎪−λ[−λ,λ]λwj&lt;0wj=0wj>0λ∂wj∣wj∣={−λwj&lt;0[−λ,λ]wj=0λwj>0 lambda partial_{w_j}|w_j|=egin{cases}-lambda&amp;w_j&lt;0\[-lambda,lambda]&amp; w_j=0\lambda&amp;w_j&gt;0end{cases} λ∂wj​​∣wj​∣=⎩⎪⎨⎪⎧​−λ[−λ,λ]λ​wj​<0wj​=0wj​>0​

整体偏导数

λ∂wj[lasso cost]=2zjwj−2ρj+⎧⎩⎨⎪⎪−λ[−λ,λ]λwj&lt;0wj=0wj>0=⎧⎩⎨⎪⎪2zjwj−2ρj−λ[−2ρj−λ,−2ρj+λ]2zjwj−2ρj+λwj&lt;0wj=0wj>0λ∂wj[lasso cost]=2zjwj−2ρj+{−λwj&lt;0[−λ,λ]wj=0λwj>0={2zjwj−2ρj−λwj&lt;0[−2ρj−λ,−2ρj+λ]wj=02zjwj−2ρj+λwj>0 lambda partial_{w_j} ext{[lasso cost]}= 2z_jw_j-2 ho_j+egin{cases}-lambda&amp;w_j&lt;0\[-lambda,lambda]&amp; w_j=0\lambda&amp;w_j&gt;0end{cases}\=egin{cases}2z_jw_j-2 ho_j-lambda&amp;w_j&lt;0\[-2 ho_j-lambda,-2 ho_j+lambda]&amp; w_j=0\2z_jw_j-2 ho_j+lambda&amp;w_j&gt;0end{cases} λ∂wj​​[lasso cost]=2zj​wj​−2ρj​+⎩⎪⎨⎪⎧​−λ[−λ,λ]λ​wj​<0wj​=0wj​>0​=⎩⎪⎨⎪⎧​2zj​wj​−2ρj​−λ[−2ρj​−λ,−2ρj​+λ]2zj​wj​−2ρj​+λ​wj​<0wj​=0wj​>0​
要想获得最有解，令

λ∂wj[lasso cost]=0λ∂wj[lasso cost]=0 lambda partial_{w_j} ext{[lasso cost]}=0 λ∂wj​​[lasso cost]=0。
解得，
wˆj=⎧⎩⎨⎪⎪(ρj+λ/2)/zj0(ρj−λ/2)/zjρj&lt;−λ/2ρj in [−λ/2,λ/2]ρj>λ/2w^j={(ρj+λ/2)/zjρj&lt;−λ/20ρj in [−λ/2,λ/2](ρj−λ/2)/zjρj>λ/2 hat w_j= egin{cases}( ho_j+lambda/2)/z_j&amp; ho_j&lt;-lambda/2\0&amp; ho_j ext{ in }[-lambda/2,lambda/2]\( ho_j-lambda/2)/z_j&amp; ho_j&gt;lambda/2end{cases} w^j​=⎩⎪⎨⎪⎧​(ρj​+λ/2)/zj​0(ρj​−λ/2)/zj​​ρj​<−λ/2ρj​ in [−λ/2,λ/2]ρj​>λ/2​

伪代码

预计算zj=∑Ni=1hj(xi)2zj=∑i=1Nhj(xi)2 z_j=sum_{i=1}^N h_j(x_i)^2 zj​=∑i=1N​hj​(xi​)2
初始化参数w（全0或随机）
循环直到收敛:

for j = 0,1,…D
$ space spacespacespace ho_j=sum_{i=1}^Nh_j(x_i)(y_i-sum_{k eq j }w_kh_k(x_i))$
    update wj    update wj space spacespacespace updatespace w_j     update wj​
选择变化幅度最大的维度进行更新

概率解释

拉普拉斯分布

随机变量X∼Laplace(μ,b)X∼Laplace(μ,b) Xsim Laplace(mu,b) X∼Laplace(μ,b)，其中μμ mu μ是位置参数，b>0b>0 b&gt;0 b>0是尺度参数。
概率密度函数为
f(x∣μ,b)=12bexp(−∣x−μ∣b)f(x∣μ,b)=12bexp(−∣x−μ∣b) f(x|mu,b)=frac{1}{2b}exp(-frac{|x-mu|}{b}) f(x∣μ,b)=2b1​exp(−b∣x−μ∣​)

MAP推导

假设ϵi∼N(0,σ2)ϵi∼N(0,σ2) epsilon_isim N(0,sigma^2) ϵi​∼N(0,σ2)，wi∼Laplace(0,1λ)wi∼Laplace(0,1λ) w_isim Laplace(0,frac{1}{lambda}) wi​∼Laplace(0,λ1​)

等价于