850. Dijkstra求最短路 II

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。

输入格式

第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式

输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出-1。

数据范围

1≤n,m≤1051≤n,m≤105,
图中涉及边长均不超过10000。

输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

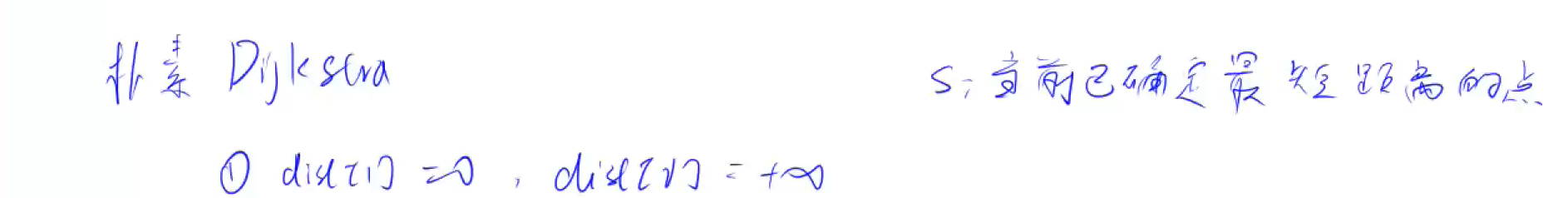
 代码实现：

//堆优化版本的dijkstra()
#include<iostream>
#include<cstring>
#include<queue>

using namespace std;


//我们需要用堆来维护所有的点的距离,维护距离的时候我们需要知道结点编号是多少
//所以堆里边存的其实是一个pair
typedef pair<int,int> PII;


const int N = 1e5 + 10;
//n,m都是1e5,属于稀疏图用邻接表
int d[N];
int h[N],ne[N],e[N],idx;
bool st[N];
//权重
int w[N];

int n,m;

void add(int a,int b,int c){
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}

int dijkstra(){
    memset(d,0x3f,sizeof d);
    d[1] = 0;
    
    //小根堆
    priority_queue<PII,vector<PII>,greater<PII>> heap;        
    //首先先把1号点放上去,因为1号点已经知道是最短距离了
    //所以先把1号点放上去跟新所有的点
    heap.push({0,1});//距离是0编号是1
    
    //当队列不为空
    while(heap.size()){
        
        //每次找到堆里边距离最小的点,也就是找到堆的起点
        auto t = heap.top();
        heap.pop();
        
        //用ver来表示结点的编号,用distance来表示结点的距离
        int ver = t.second,distance = t.first;
        
        //如果ver这个结点之前已经出来过了,说明当前这个点是一个冗余备份
        //所以没有必要再处理它了,直接continue就完事了
        if(st[ver]) continue;
        st[ver] = true;
        //后面就用当前这个点更新这个点就完事了
        //更新的话就遍历一下所有的邻边
        for(int i = h[ver];i != -1;i=ne[i]){
            //用j存储该结点的编号
            int j = e[i];
            
            //更新
            //如果当前距离d[j]大于从t过来的距离的话,就把d[j]更新下
            if(d[j] > distance + w[i]){
                //更新较小的距离
                d[j] = distance + w[i]; 
                
                //再将j这个点放在优先队列里边去
                heap.push({d[j],j});
            }
        }
    }
    
    
    
    if(d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}

int main(){
    cin >> n >> m;
    
    //邻接表初始化表头
    memset(h,-1,sizeof h);
    
    while(m --){
        int x,y,z;
        cin >> x >> y >> z;
        add(x,y,z);
    }
    
    //用邻接表不用去除重边，因为算法本身保证了最短路，所以不需要对重边做特殊的处理
    cout << dijkstra() << endl;
    return 0;
}