A. Sereja and Mugs
time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output
Sereja showed an interesting game to his friends. The game goes like that. Initially, there is a table with an empty cup and n water mugs on it. Then all players take turns to move. During a move, a player takes a non-empty mug of water and pours all water from it into the cup. If the cup overfills, then we assume that this player lost.
As soon as Sereja's friends heard of the game, they wanted to play it. Sereja, on the other hand, wanted to find out whether his friends can play the game in such a way that there are no losers. You are given the volumes of all mugs and the cup. Also, you know that Sereja has (n - 1) friends. Determine if Sereja's friends can play the game so that nobody loses.
The first line contains integers n and s (2 ≤ n ≤ 100; 1 ≤ s ≤ 1000) — the number of mugs and the volume of the cup. The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 10). Number ai means the volume of the i-th mug.
In a single line, print "YES" (without the quotes) if his friends can play in the described manner, and "NO" (without the quotes) otherwise.
3 4
1 1 1
YES
3 4
3 1 3
YES
3 4
4 4 4
NO
题意 : 大意大概是有很多n个小杯,1大杯,每个小杯的容积以及大杯的容积都知道了,游戏规则是,每个人拿一个非空的小杯,把水全部倒大杯里,如果谁倒的时候大杯满了,谁就输,然后她的(n-1)个朋友要玩儿,问你有没有一种倒水的方法使得没有人会输,如果没有输出NO。
思路 : 一开始以为她自己也玩儿,就不知道第二组样例为什么对了,后来又看了一遍题,觉得应该是光朋友玩儿,就试了一下儿,结果对了。。。。。


1 #include <stdio.h> 2 #include <iostream> 3 #include <algorithm> 4 5 using namespace std ; 6 7 int a[110] ; 8 9 int main() 10 { 11 int n,s ; 12 while(~scanf("%d %d",&n,&s)) 13 { 14 for(int i = 0 ; i < n ; i++) 15 scanf("%d",&a[i]) ; 16 sort(a,a+n) ; 17 int sum = 0 ; 18 bool flag = false ; 19 for(int i = 0 ; i < n-1 ; i++) 20 { 21 sum += a[i] ; 22 if(sum > s) 23 { 24 flag = true ; 25 break ; 26 } 27 } 28 if(flag) 29 puts("NO") ; 30 else puts("YES") ; 31 } 32 return 0 ; 33 }
B. Sereja and Mirroring
time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output
Let's assume that we are given a matrix b of size x × y, let's determine the operation of mirroring matrix b. The mirroring of matrix b is a2x × y matrix c which has the following properties:
- the upper half of matrix c (rows with numbers from 1 to x) exactly matches b;
- the lower half of matrix c (rows with numbers from x + 1 to 2x) is symmetric to the upper one; the symmetry line is the line that separates two halves (the line that goes in the middle, between rows x and x + 1).
Sereja has an n × m matrix a. He wants to find such matrix b, that it can be transformed into matrix a, if we'll perform on it several(possibly zero) mirrorings. What minimum number of rows can such matrix contain?
The first line contains two integers, n and m (1 ≤ n, m ≤ 100). Each of the next n lines contains m integers — the elements of matrix a. The i-th line contains integers ai1, ai2, ..., aim (0 ≤ aij ≤ 1) — the i-th row of the matrix a.
In the single line, print the answer to the problem — the minimum number of rows of matrix b.
4 3
0 0 1
1 1 0
1 1 0
0 0 1
2
3 3
0 0 0
0 0 0
0 0 0
3
8 1
0
1
1
0
0
1
1
0
2
In the first test sample the answer is a 2 × 3 matrix b:
001
110
If we perform a mirroring operation with this matrix, we get the matrix a that is given in the input:
001110
110
001
题意 :这个破题读了好久,我严重怀疑我近段时间的英语水平。就是说一个大小为x*y的矩阵b的mirroring定义为一个大小为2x*y的矩阵,前x行与b相同,后x行与前x行对称,然后给你一个n*m的矩阵,让你求一个矩阵b,使得b经过几次或0次mirroring后能够得到a,让你输出成立的b中,行最少的那一个。


1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 6 using namespace std ; 7 8 int a[110][110] ; 9 char str[110][110] ; 10 11 int main() 12 { 13 int n,m ; 14 while(~scanf("%d %d",&n,&m)) 15 { 16 for(int i = 0 ; i < n ; i++) 17 for(int j = 0 ; j < m ; j++) 18 scanf("%d",&a[i][j]) ; 19 if(n % 2) 20 { 21 cout<<n<<endl ; 22 continue ; 23 } 24 int mid ; 25 while(true) 26 { 27 mid = n >> 1 ; 28 bool flag = true; 29 for(int i = 0 ; i < mid ; i++) 30 { 31 int j = n-i-1 ; 32 for(int k = 0 ; k < m ; k++) 33 { 34 if(a[i][k] != a[j][k]) 35 { 36 flag = false ; 37 break ; 38 } 39 } 40 if(!flag) 41 break ; 42 } 43 if(!flag) 44 { 45 printf("%d ",mid*2) ; 46 break ; 47 } 48 else 49 { 50 if(mid % 2) 51 { 52 cout<<mid<<endl ; 53 break ; 54 } 55 else 56 n = n >> 1 ; 57 } 58 } 59 } 60 return 0 ; 61 }
C. Sereja and Swaps
time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output
As usual, Sereja has array a, its elements are integers: a[1], a[2], ..., a[n]. Let's introduce notation:
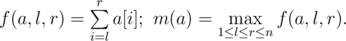
A swap operation is the following sequence of actions:
- choose two indexes i, j (i ≠ j);
- perform assignments tmp = a[i], a[i] = a[j], a[j] = tmp.
What maximum value of function m(a) can Sereja get if he is allowed to perform at most k swap operations?
The first line contains two integers n and k (1 ≤ n ≤ 200; 1 ≤ k ≤ 10). The next line contains n integers a[1], a[2], ..., a[n] ( - 1000 ≤ a[i] ≤ 1000).
In a single line print the maximum value of m(a) that Sereja can get if he is allowed to perform at most k swap operations.
10 2
10 -1 2 2 2 2 2 2 -1 10
32
5 10
-1 -1 -1 -1 -1
题意 : 给了两个公式能够求出m(a),然后允许最多交换k次,求其中的最大的m(a)。


1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <algorithm> 5 #include <vector> 6 7 using namespace std ; 8 9 int a[1010] ; 10 11 int main() 12 { 13 int n ,k; 14 while(~scanf("%d %d",&n,&k)) 15 { 16 for(int i = 1 ; i <= n ; i++) 17 scanf("%d",&a[i]) ; 18 int maxx = -9999999,sum ; 19 for(int i = 1 ; i <= n ; i++) 20 { 21 for(int j = i ; j <= n ; j++) 22 { 23 sum = 0 ; 24 vector<int > v ,u; 25 for(int h = i ; h <= j ; h++) 26 { 27 v.push_back(a[h]) ; 28 sum += a[h] ; 29 } 30 maxx = max(maxx,sum) ; 31 for(int h = 1 ; h <= n ; h++) 32 { 33 if(h < i || h > j) 34 u.push_back(a[h]) ; 35 } 36 sort(v.begin(),v.end()) ; 37 sort(u.begin(),u.end()) ; 38 reverse(u.begin(),u.end()) ; 39 for(int h = 1 ; h <= k && h <= v.size() && h <= u.size() ; h++)//枚举交换次数 40 { 41 if(v[h-1] < u[h-1]) 42 { 43 sum -= v[h-1] ; 44 sum += u[h-1] ; 45 maxx = max(sum,maxx) ; 46 } 47 } 48 } 49 } 50 printf("%d ",maxx) ; 51 } 52 return 0 ; 53 }