Codeforces Round #242 (Div. 2) A～C

题目链接

A. Squats

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

Pasha has many hamsters and he makes them work out. Today, n hamsters (n is even) came to work out. The hamsters lined up and each hamster either sat down or stood up.

For another exercise, Pasha needs exactly  hamsters to stand up and the other hamsters to sit down. In one minute, Pasha can make some hamster ether sit down or stand up. How many minutes will he need to get what he wants if he acts optimally well?

Input

The first line contains integer n (2 ≤ n ≤ 200; n is even). The next line contains n characters without spaces. These characters describe the hamsters' position: the i-th character equals 'X', if the i-th hamster in the row is standing, and 'x', if he is sitting.

Output

In the first line, print a single integer — the minimum required number of minutes. In the second line, print a string that describes the hamsters' position after Pasha makes the required changes. If there are multiple optimal positions, print any of them.

Sample test(s)

input

4
xxXx

output

1
XxXx

input

2
XX

output

1
xX

input

6
xXXxXx

output

0
xXXxXx

题意 ： X代表站着，x代表蹲着，要求n只中正好有一半是蹲着一半是站着，让一只仓鼠由蹲变为站或由站变为蹲需要1分钟，问最少需要多少分钟能够达到要求。

思路 ： 水题不详述，一开始还因为题中的那个1分钟让一些仓鼠换状态，有一些疑惑，后来就直接当成让一个，然后就过了。

#include <stdio.h>
#include <string.h>
#include <iostream>

using namespace std ;
char sh[210] ;
int main()
{
    int n ;
    while(~scanf("%d",&n))
    {
        scanf("%s",sh) ;
        int cnt = 0 ;
        for(int i = 0 ; i < n ; i++)
            if(sh[i] == 'X')
                cnt++ ;
        if(cnt == n/2)
        {
            printf("0
%s
",sh) ;
        }
        else if(cnt > n/2)
        {
            printf("%d
",cnt-n/2) ;
            for(int i = 0 ,k = 0; i < n && k < cnt-n/2 ; i++)
                if(sh[i] == 'X')
                {
                    sh[i] = 'x';
                    k++ ;
                }
            printf("%s
",sh) ;
        }
        else if(cnt < n/2)
        {
            printf("%d
",n/2-cnt) ;
            for(int i = 0 ,k = 0; i < n && k < n/2-cnt ; i++)
                if(sh[i] == 'x')
                {
                    sh[i] = 'X';
                    k++ ;
                }
            printf("%s
",sh) ;
        }
    }
    return 0 ;
}

B. Megacity

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

The administration of the Tomsk Region firmly believes that it's time to become a megacity (that is, get population of one million). Instead of improving the demographic situation, they decided to achieve its goal by expanding the boundaries of the city.

The city of Tomsk can be represented as point on the plane with coordinates (0; 0). The city is surrounded with n other locations, the i-th one has coordinates (xi, yi) with the population of ki people. You can widen the city boundaries to a circle of radius r. In such case all locations inside the circle and on its border are included into the city.

Your goal is to write a program that will determine the minimum radius r, to which is necessary to expand the boundaries of Tomsk, so that it becomes a megacity.

Input

The first line of the input contains two integers n and s (1 ≤ n ≤ 103; 1 ≤ s < 106) — the number of locatons around Tomsk city and the population of the city. Then n lines follow. The i-th line contains three integers — the xi and yi coordinate values of the i-th location and the number ki of people in it (1 ≤ ki < 106). Each coordinate is an integer and doesn't exceed 104 in its absolute value.

It is guaranteed that no two locations are at the same point and no location is at point (0; 0).

Output

In the output, print "-1" (without the quotes), if Tomsk won't be able to become a megacity. Otherwise, in the first line print a single real number — the minimum radius of the circle that the city needs to expand to in order to become a megacity.

The answer is considered correct if the absolute or relative error don't exceed 10 - 6.

Sample test(s)

input

4 999998
1 1 1
2 2 1
3 3 1
2 -2 1

output

2.8284271

input

4 999998
1 1 2
2 2 1
3 3 1
2 -2 1

output

1.4142136

input

2 1
1 1 999997
2 2 1

output

-1

题意 ： 周围有n个城市，这个城市目前有k个人，这个城市要往外扩充，来让人数达到1000000，以0，0为圆心，问你找一个半径为r的圆，要使r尽量小并且这个城市扩充之后的人数至少为1000000 。

思路 ： 把这n个城市到圆心的距离排一下序，从最近的开始加。

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <iostream>

using namespace std ;

struct node
{
    double x,y ;
    int num ;
} p[1100];

int cmp(const node &a,const node &b)
{
    if(sqrt(a.x*a.x+a.y*a.y)  ==  sqrt(b.x*b.x+b.y*b.y))
        return a.num > b.num ;
    return sqrt(a.x*a.x+a.y*a.y) < sqrt(b.x*b.x+b.y*b.y) ;
}
int main()
{
    int n , k;
    while(~scanf("%d %d",&n,&k))
    {
        int sum = 0 ;
        for(int i = 0 ; i < n ; i++)
        {
            scanf("%lf %lf %d",&p[i].x,&p[i].y,&p[i].num) ;
            sum += p[i].num ;
        }
        if(sum + k < 1000000)
        {
            printf("-1
") ;
            continue ;
        }
        sort(p,p+n,cmp) ;
        int cnt = 1000000-k,j,i ;
        for(i = 0 ,j = cnt; i < n && j >= 0 ; i++)
        {
                if(p[i].num >= j)
                    break ;
                else {
                    j -= p[i].num ;
                }

        }
        printf("%.7lf
",sqrt(p[i].x*p[i].x+p[i].y*p[i].y)) ;
    }
    return 0 ;
}

C. Magic Formulas

time limit per test:1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

People in the Tomskaya region like magic formulas very much. You can see some of them below.

Imagine you are given a sequence of positive integer numbers p1, p2, ..., pn. Lets write down some magic formulas:

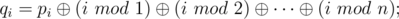
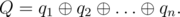
Here, "mod" means the operation of taking the residue after dividing.

The expression 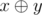 means applying the bitwise xor (excluding "OR") operation to integers x and y. The given operation exists in all modern programming languages. For example, in languages C++ and Java it is represented by "^", in Pascal — by "xor".

People in the Tomskaya region like magic formulas very much, but they don't like to calculate them! Therefore you are given the sequence p, calculate the value of Q.

Input

The first line of the input contains the only integer n (1 ≤ n ≤ 106). The next line contains n integers: p1, p2, ..., pn (0 ≤ pi ≤ 2·109).

Output

The only line of output should contain a single integer — the value of Q.

Sample test(s)

input

3
1 2 3

output

3

题意 ： 给你p1,p2.....pn,根据给定的两个式子，让你求出Q 。

思路 ： 如果直接求肯定超时，所以要另辟蹊径。不能一行一行的异或，要一列一列的异或，等列出表就可以轻易的观察出规律。还有一个数异或上0还是本身。

从这个表中可以看出每一列的规律，所以异或的时候一列一列的去异或，因为如果你异或上两个相同的数还是本身，所以每一列要找重复周期，如果周期为偶数，那就不用异或，如果为偶数但是余数不为0，可以看出3那一列就是周期数为偶数但是余数为1，就要再异或上这个1，当然有的时候剩的不止是1，但是剩下的数一定从一开始，所以要提前打个表。

我的代码

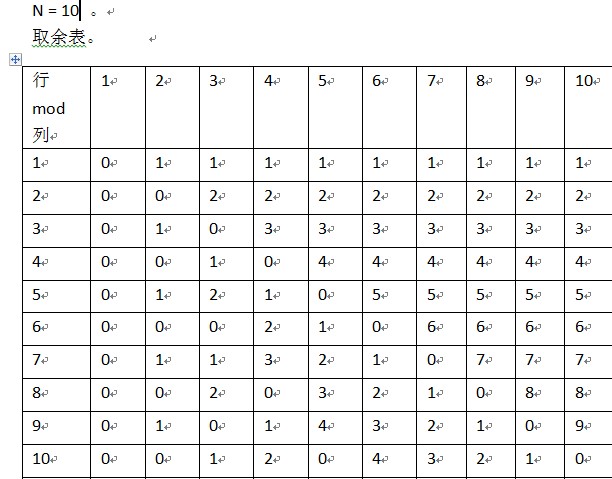
#include <stdio.h>
#include <iostream>
#include <string.h>

using namespace std ;

long long a[1000010] ;
long long m ;

void table()
{
    a[0] = 0 ;
    a[1] = 1 ;
    for(int i = 2 ; i < 1000010 ; i++)
        a[i] = a[i-1] ^ i ;
}

int main()
{
    int n ;
    table() ;
    while(~scanf("%d",&n))
    {
        long long sum = 0 ;
        for(int i = 1 ; i <= n ; i++)
        {
            scanf("%I64d",&m) ;
            sum = sum ^ m ;
        }
        for(int i = 2 ; i <= n ; i++)
        {
            int rest = n % i ;
            int t = n / i ;
            if(t % 2)
            {
                sum ^= a[i-1] ;
                if(rest != 0)
                sum ^= a[rest] ;
            }
            else
            {
                if(rest != 0)
                    sum ^= a[rest] ;
            }
        }
        printf("%I64d
",sum) ;
    }
    return 0 ;
}

这个代码其实有更为简单的写法。。。。。

#include<stdio.h>

long long sum,a[1234567],n,m;

int main()
{
    while(~scanf("%I64d",&n))
    {
        for(int i = 1 ; i <= n ; i++)
        {
            a[i] = a[i-1] ^ i ;
            scanf("%I64d",&m) ;
            sum ^= m ^ a[n % i] ^ ( n / i % 2 ? a[i-1] : 0 );
        }
        printf("%I64d
",sum) ;
    }
    return 0;
}

很神奇有没有。。。。