参考文献:J. M. Thijssen, 《Computational Physics》
1. Formalism
为了简化,设一维谐振子的哈密顿量为
\[\hat{H} = - \frac{d^2}{dx^2} + x^2
\]
引入拟设波函数
\[\psi(x, \alpha) = e^{-\alpha x^2},
\]
定义局域能量
\[E_L(x, \alpha) = \frac{ \hat{H} \psi(x, \alpha) }{ \psi(x, \alpha)},
\]
如果 \(\alpha\) 的值恰当,使得 \(\psi(x,\alpha)\) 是 \(\hat{H}\) 的本征态,则 \(\forall x, E_L(x,\alpha) = \epsilon\)。
变分法中的“平均能量”为
\[\langle E(\alpha) \rangle = \int E_L(x, \alpha) \psi(x,\alpha)^2 dx.
\]
所以,设置大量的随机行者,用 Markov-Metropolis 方法,使得行者的分布密度 \(\rho(x,\alpha) \propto \psi(x,\alpha)^2\),然后做 \(E_L(x,\alpha)\)的抽样平均,即得 \(\langle E(\alpha) \rangle\) 的近似值。
另外,可以观察抽样方差 \(\sigma^2(\alpha) = \langle E(\alpha)^2 \rangle - \langle E(\alpha) \rangle^2\) 与 \(\alpha\) 的函数关系。如果 \(\alpha\) 恰当,使得 \(\psi(x,\alpha)\) 是 \(\hat{H}\) 的本征态,则 \(\sigma^2(\alpha) = 0\),如果 \(\alpha\) 不够理想,就有 \(\sigma^2(\alpha) > 0\)。
2. 代码
# 一维谐振子求基态能量
import numpy as np
import matplotlib.pyplot as plt
# trial wave: psi = e^{ -alpha x^2 }
# H = - d^2/dx^2 + x*x
import scipy.integrate
def psi(x,alpha):
return np.exp( -alpha * x * x )
#help(scipy.integrate.quad); exit(1)
def plotpsi2(alpha):
C = scipy.integrate.quad(psi,-np.inf,np.inf,args=(2*alpha,))[0]
x = np.arange(-3,3,0.1)
y = [ psi(t,alpha) * psi(t,alpha) / C for t in x ]
plt.plot(x,y)
#plotpsi2(0.4); exit(1)
# d/dx psi = -2 alpha x e^{- alpha * x * x }
# d^2 /d x^2 psi = -2 alpha + 4 * alpha^2 x^2 e^{-alpha x^2}
# ( - d^2/dx^2 + x*x ) psi / psi = 2 alpha + (- 4 alpha^2 + 1) x^2
def EL( alpha, x):
return 2*alpha + (1-4*alpha*alpha)*x*x
# if alpha = 0.5, EL(alpha, x) = 1
# if alpha = 0.6, EL(alpha, x) = 1.2 - 0.44 * x*x
def Accept( x1, x2, alpha, psi ):
if( abs(x2)>3 ): return 0
p = ( psi(x2,alpha) / psi(x1,alpha) )**2
#print("p=",p)
if p>1: return 1
else: return p
def tryonestep(x,nwalker,h,alpha):
for j in range(nwalker):
step = h * ( 2*np.random.randint(0,2) - 1 )
A = Accept(x[j], x[j] + step, alpha, psi)
if (np.random.random() < A):
x[j] += step
def ELsampling( alpha, nwalker, psi, EL, a, b, h, nstep ):
x = (b-a)*np.random.random(nwalker) + a # 初始位置
for i in range(nstep):
tryonestep(x, nwalker, h, alpha)
#plotpsi2(alpha);
#plt.hist(x, bins=np.arange(-3.1,3.1,0.2), rwidth=0.8, density="True" ); plt.show()
#print( "alpha = ",alpha, " <E>_L = ", np.average( [ EL(alpha,t) for t in x ] ) )
return [ EL(alpha,t) for t in x ]
aveE = []; aveE2 = [] # < E >, < E^2 >
Alpha = np.arange(0.4,0.6,0.02)
for alpha in Alpha:
ELsample = ELsampling(alpha, 1000, psi, EL, a=-3, b=3, h=0.2, nstep=100 )
aveE.append( np.average(ELsample) )
aveE2.append( np.average([t*t for t in ELsample ]) )
sigma2 = aveE2 - np.array([t*t for t in aveE])
plt.plot(Alpha, sigma2)
plt.show()
3. 结果
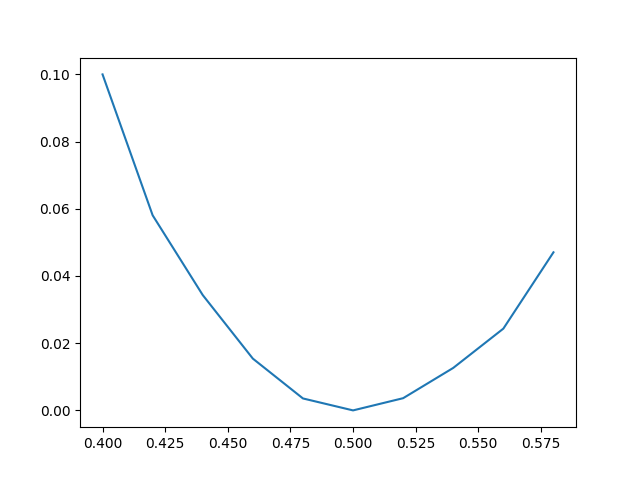
做出来 \(\sigma^2(\alpha) \sim \alpha\) 的图如下。可见 \(\alpha=0.5\) 是最优参数。
4. 小结
- 代码中有绘制 \(\rho(x,\alpha)\) 的片段,可以用于观察随机行者在接受概率的指引下收敛于 \(\rho(x,\alpha)\) 的速度。在我的试验中,行者处在 \(-3, -2.8, \cdots, 2.8, 3.0\) 这些格点上,一共大约 30 个位置,大约 100 步随机行走后,行者分布就已经收敛至 \(\rho(x, \alpha)\) 曲线。
- \(\langle E(\alpha) \rangle\) 远远没有 \(\sigma^2(\alpha)\) 犀利。上面的代码以及其中的参数跑出来的 \(\langle E(\alpha) \rangle\) 曲线非常磕碜,但是上面展示的 \(\sigma^2(\alpha)\) 曲线就非常规整,且容易反映出问题。如果你开个根号,画 \(\sigma \sim \alpha\),就会更加 sharp。