gsl库
在ubuntu下,只需
sudo apt-get install libgsl23
或者
sudo apt-get install libgsl-dev
即可安装
gsl_multimin_fdfminimizer
众所周知,共轭梯度法是很有效的多元函数找极值算法。gsl是gnu scientific library的缩写,gnu是GNU's not Unix的缩写,是个自由操作系统统称,下面有很多软件,gsl是其中之一。gsl_multimin_fdfminimizer 是gsl中的共轭梯度法求解器,如下是使用代码示例。
使用步骤为:
- 定义函数(f(vec{x}, void * params)),params是用到的其他参数,都用一个指针传递。
- 定义一阶导数(f'(vec{x}, void * params))
- 把(f, f')集成在一块,定义my_fdf
- 定义并初始化一个 gsl_multimin_fdfminimizer 对象,然后进行迭代,直到在某处梯度矢量的绝对值小于某个值。
代码示例
#include<iostream>
using namespace std;
#include<gsl/gsl_multimin.h>
#include<gsl/gsl_sf_bessel.h>
int count_myf = 0;
/* Paraboloid centered on (p[0],p[1]), with
scale factors (p[2],p[3]) and minimum value p[4] */
double my_f (const gsl_vector *v, void *params)
{
count_myf ++;
double x, y;
double *p = (double *)params;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
return p[2] * (x - p[0]) * (x - p[0]) +
p[3] * (y - p[1]) * (y - p[1]) + p[4];
}
/* The gradient of f, df = (df/dx, df/dy). */
void my_df (const gsl_vector *v, void *params, gsl_vector *df)
{
double x, y;
double *p = (double *)params;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
gsl_vector_set(df, 0, 2.0 * p[2] * (x - p[0]));
gsl_vector_set(df, 1, 2.0 * p[3] * (y - p[1]));
}
/* Compute both f and df together. */
void my_fdf (const gsl_vector *x, void *params, double *f, gsl_vector *df)
{
*f = my_f(x, params);
my_df(x, params, df);
}
int main(){
// define the multi-var function to be optimized
gsl_multimin_function_fdf my_func;
/* Paraboloid center at (1,2), scale factors (10, 20), minimum value 30 */
double p[5] = { 1.0, 2.0, 10.0, 20.0, 30.0 };
my_func.n = 2; /* number of function components */
my_func.f = &my_f;
my_func.df = &my_df;
my_func.fdf = &my_fdf;
my_func.params = (void *)p;
// set initial position x
gsl_vector *x;
x = gsl_vector_alloc(2);
gsl_vector_set( x, 0, 5.0 );
gsl_vector_set( x, 1, 7.0 );
cout<<" f(1,2) = "<< my_func.f( x, my_func.params ) <<endl;
// set minimization type
const gsl_multimin_fdfminimizer_type *T;
T = gsl_multimin_fdfminimizer_conjugate_fr;
// set minimizer
gsl_multimin_fdfminimizer *s;
s = gsl_multimin_fdfminimizer_alloc( T, 2 );
gsl_multimin_fdfminimizer_set( s, &my_func, x, 0.01, 1E-4 );
int iter = 0, status;
do{
iter++;
status = gsl_multimin_fdfminimizer_iterate( s );
if( status ) break;
status = gsl_multimin_test_gradient( s->gradient, 1E-3 );
if( status == GSL_SUCCESS )
printf( " Minimum found at :
" );
printf( "%5d %.10f %.10f %10.5f
", iter, gsl_vector_get( s->x, 0 ), gsl_vector_get( s->x, 1 ), s->f );
}
while ( status == GSL_CONTINUE && iter < 100 );
cout<<" count_myf = "<<count_myf<<endl;
gsl_multimin_fdfminimizer_free( s );
gsl_vector_free( x );
return 0;
}
编译、运行、结果
编译:
g++ test_multimin_conjugate_gradient.cpp -lgsl -lblas
运行:
./a.out
结果:
f(1,2) = 690
1 4.9962860932 6.9907152331 687.84780
2 4.9888582797 6.9721456993 683.55456
3 4.9740026527 6.9350066316 675.01278
4 4.9442913985 6.8607284964 658.10798
5 4.8848688903 6.7121722258 625.01340
6 4.7660238739 6.4150596847 561.68440
7 4.5283338410 5.8208346026 446.46694
8 4.0529537753 4.6323844382 261.79422
9 3.1021936438 2.2554841096 75.49762
10 2.8518518519 1.6296296296 67.03704
11 2.1908758523 1.7618248295 45.31640
12 0.8689238532 2.0262152294 30.18555
Minimum found at :
13 1.0000000000 2.0000000000 30.00000
count_myf = 28
所以一共取了13个点,(f(vec{x}))函数被调用了28次。收敛的很好,误差很小。把这些点画在二维平面上:
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('screen')
x, y = [], []
for t in data:
x.append(t[0])
y.append(t[1])
fig, ax = plt.subplots()
ax.scatter(x,y)
#建立步长为0.01,即每隔0.01取一个点
step = 0.01
x = np.arange(-10,10,step)
y = np.arange(-10,10,step)
#也可以用x = np.linspace(-10,10,100)表示从-10到10,分100份
#将原始数据变成网格数据形式
X,Y = np.meshgrid(x,y)
#写入函数,z是大写
Z = 10*(X-1)**2 + 20*(Y-2)**2 + 30
#设置打开画布大小,长10,宽6
#plt.figure(figsize=(10,6))
#填充颜色,f即filled
#ax.contourf(X,Y,Z)
#画等高线
ax.contour(X,Y,Z)
plt.show()
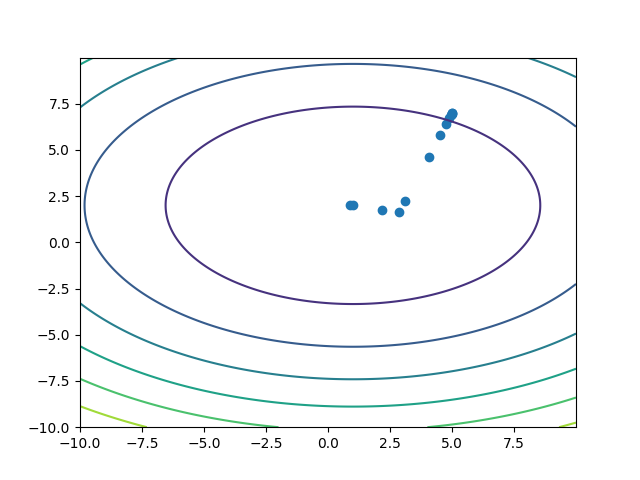
如果仔细算斜率,会发现确实只有两个下降方向,与共轭梯度理论一致。更重要的是,一共只取了13个点。gsl的文档中有说明,每次一维最优化只需要达到很低的精度即可,然而也还是能保证一共只需2个下降方向,这大概是他们设计的算法的力量。这是使用gsl库,而不自己重写共轭梯度法的好处。
自由参数个数(n=50,100,150,...,1000)
下面的代码测试(n)值更大时,迭代次数的增长规律,(n, iter)的值被输出到文件。
#include<iostream>
using namespace std;
#include<iomanip>
#include<fstream>
#include<gsl/gsl_multimin.h>
#include<gsl/gsl_sf_bessel.h>
int n = 100;
double my_f (const gsl_vector *v, void *params)
{
double *p = (double *)params;
double x, f = 0;
for(int i=0;i<n;i++){
x = gsl_vector_get(v, i);
f += p[n+i] * ( x - p[i] ) * (x - p[i] );
}
f += p[ 2*n ];
return f;
}
/* The gradient of f, df = (df/dx, df/dy). */
void my_df (const gsl_vector *v, void *params,
gsl_vector *df)
{
double x;
double *p = (double *)params;
for(int i=0;i<n;i++){
x = gsl_vector_get(v, i);
gsl_vector_set(df, i, 2.0 * p[n+i] * ( x - p[i] ) );
}
}
/* Compute both f and df together. */
void my_fdf (const gsl_vector *x, void *params,
double *f, gsl_vector *df)
{
*f = my_f(x, params);
my_df(x, params, df);
}
void minimizer( ofstream & fout ){
// define the multi-var function to be optimized
gsl_multimin_function_fdf my_func;
double *p = new double [ 2*n + 1 ];
for(int i=0;i<n;i++){
p[i] = i+1; p[n+i] = 10*i+10;
}
p[2*n] = 100;
my_func.n = n; /* number of function components */
my_func.f = &my_f;
my_func.df = &my_df;
my_func.fdf = &my_fdf;
my_func.params = (void *)p;
// set initial position x
gsl_vector *x;
x = gsl_vector_alloc(n);
for(int i=0;i<n;i++) gsl_vector_set( x, i, 10.0 );
// set minimization type
const gsl_multimin_fdfminimizer_type *T;
T = gsl_multimin_fdfminimizer_conjugate_fr;
// set minimizer
gsl_multimin_fdfminimizer *s;
s = gsl_multimin_fdfminimizer_alloc( T, n );
gsl_multimin_fdfminimizer_set( s, &my_func, x, 0.01, 1E-4 );
int iter = 0, status;
do{
iter++;
status = gsl_multimin_fdfminimizer_iterate( s );
if( status ) break;
status = gsl_multimin_test_gradient( s->gradient, 1E-3 );
if( status == GSL_SUCCESS ){
fout<<n<<" "<<iter<<endl;
printf( " n=%d, Minimum found after %d iterations
", n, iter );
/*
cout<<" "<<iter << setprecision(14);
for(int j=0;j<n;j++) cout<<" "<< gsl_vector_get( s->x, j );
cout<<" "<< s->f <<endl;
*/
}
}
while ( status == GSL_CONTINUE && iter < 10000 );
gsl_multimin_fdfminimizer_free( s );
gsl_vector_free( x );
}
int main(){
ofstream fout("iterater.txt");
for(n=50;n<=1000;n+=50) minimizer( fout );
fout.close();
return 0;
}
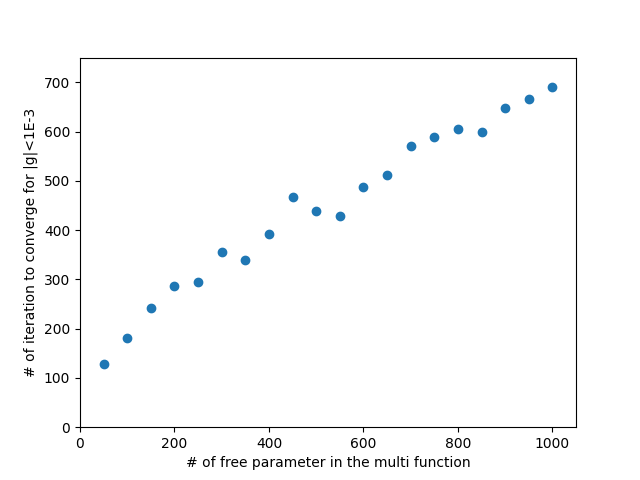
从文件中读取(n,iter)的值以后,作图如下
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('../test/gsl/iterater.txt')
x, y = [], []
for t in data:
x.append(t[0])
y.append(t[1])
fig, ax = plt.subplots()
ax.scatter(x,y)
ax.set_xlim(0,1050)
ax.set_ylim(0,750)
ax.set_xlabel("# of free parameter in the multi function")
ax.set_ylabel("# of iteration to converge for |g|<1E-3")
plt.show()
条件优化:控制(x^2+y^2 approx 1)
优化函数:(f(vec{r}) = frac{ 10 ( x^2 + 2 y^2 ) }{ x^2 + y^2 }),并且控制(|vec{r}|)不要偏离1太远。
策略:加上一个函数:(g(vec{r}) = 100 ( |vec{r}| - 1 )^2, if |vec{r}|>1, 0<|vec{r}| < 0.5; 0, else),人为地抬高(vec{r})太小或太大的区域,以此完成目标。
#include<iostream>
using namespace std;
#include<iomanip>
#include<fstream>
#include<gsl/gsl_multimin.h>
#include<gsl/gsl_sf_bessel.h>
double my_f (const gsl_vector *v, void *params)
{
double x, y, norm, z ;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
norm = x*x + y*y;
z = 10 * ( x*x + 2*y*y ) / ( x*x + y*y );
if( norm > 1 || norm < 0.5 ) return z + 100 * (norm-1) * (norm-1);
else return z;
}
/* The gradient of f, df = (df/dx, df/dy). */
void my_df (const gsl_vector *v, void *params,
gsl_vector *df)
{
double x, y, norm, z;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
norm = x*x + y*y;
z = - 20 * x * y * y / ( x*x + y*y ) / ( x*x + y*y );
if ( norm >= 1 || norm <= 0.5 ) z += 400 * x * ( norm -1 );
gsl_vector_set(df, 0, z );
z = 20 * x * x * y / ( x*x + y*y ) / ( x*x + y*y );
if ( norm >= 1 || norm <= 0.5 ) z += 400 * y * ( norm -1 );
gsl_vector_set(df, 1, z );
}
/* Compute both f and df together. */
void my_fdf (const gsl_vector *x, void *params,
double *f, gsl_vector *df)
{
*f = my_f(x, params);
my_df(x, params, df);
}
/*
* int n: number of variables
* double * x_init: initial position
* double step: size of the first trial step
* double tol: 1-d optimization is finished when gradient g is perpendicular to the search direction p to a relative accuracy tol: vec{p} cdot vec{g} < tol * | vec{p} | * | vec{g} |, 0.1 should be enough for most purposes, 0 means absolute orthogonal which is expensive.
* double epsabs: criteria of whether the norm of gradient is small enough: |g| < epsabs
* const int max_iter: max iteration number
*/
void GSL_fdf_minimizer( int n, double *x_init, double step, double tol, double epsabs, const int max_iter,
double (*m_f)( const gsl_vector *, void *), void (*my_df)( const gsl_vector *, void *, gsl_vector *), void (*my_fdf)( const gsl_vector *, void *, double *, gsl_vector *) ){
// define the multi-var function to be optimized
gsl_multimin_function_fdf my_func;
my_func.n = n; /* number of function components */
my_func.f = my_f;
my_func.df = my_df;
my_func.fdf = my_fdf;
//my_func.params = (void *)p;
// set initial position x
gsl_vector *x;
x = gsl_vector_alloc(n);
for(int i=0;i<n;i++) gsl_vector_set( x, i, x_init[i] );
// set minimization type
const gsl_multimin_fdfminimizer_type *T;
T = gsl_multimin_fdfminimizer_conjugate_fr;
// set minimizer
gsl_multimin_fdfminimizer *s;
s = gsl_multimin_fdfminimizer_alloc( T, n );
gsl_multimin_fdfminimizer_set( s, &my_func, x, step, tol );
int iter = 0, status;
do{
iter++;
status = gsl_multimin_fdfminimizer_iterate( s );
if( status ) break;
status = gsl_multimin_test_gradient( s->gradient, epsabs );
// test the norm of gradient against tolerance epsabs, returns GSL_SUCCESS if |g| < epsabs
if( status == GSL_SUCCESS ){
printf( " n=%d, Minimum found after %d iterations
", n, iter );
}
cout<<" "<<iter ;//<< setprecision(14);
for(int j=0;j<n;j++) cout<<" "<< gsl_vector_get( s->x, j );
cout<<" "<< s->f <<endl;
}
while ( status == GSL_CONTINUE && iter < max_iter );
if( iter == max_iter ) cout<<" Failed to converge, after "<<max_iter<<" iterations"<<endl;
gsl_multimin_fdfminimizer_free( s );
gsl_vector_free( x );
}
int main(){
ofstream fout("iterater.txt");
int n = 2; // 2-variable
double x_init[] = {5,7};
double step = 0.1;
double tol = 0.001;
double epsabs = 1E-3;
int max_iter = 1E6;
GSL_fdf_minimizer( n, x_init, step, tol, epsabs, max_iter, my_f, my_df, my_fdf );
fout.close();
return 0;
}
运行结果:
1 4.94188 6.91863 508236
2 4.82563 6.75588 461446
3 4.59314 6.43038 377587
4 4.12815 5.7794 244478
5 3.19817 4.47742 85722.6
6 1.33822 1.87346 1866.22
7 0.534537 0.748294 16.6213
8 0.894672 0.491013 12.4873
9 0.683379 0.192045 10.7319
10 0.696522 -0.173815 10.5862
11 0.694989 -0.131158 10.3439
12 0.702905 -0.0892135 10.1585
13 0.718737 -0.00532433 10.0005
n=2, Minimum found after 14 iterations
14 0.719741 -3.544e-11 10
与理论预期一致:收敛在(y=0)的点上,并且(|vec{r}| = 0.719741)也没有偏离1很远。