1、构成:
符号位、尾数、基数、指数

2、浮点数二进制表示
基数为2,只保留符号位(s)、尾数(m)、指数(e):
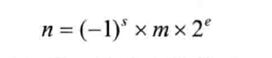
3、浮点数格式:
单精度、双精度和扩展精度。
单精度浮点数为32位:
对应于C语言中的float,其中包含一位符号位S,8位指数位E和23位尾数位M,尽管M有23位,但他表示小数点之后的二进制小数,例如M为0110,其实是0.0110,这时因为标准规定小数点左边还有一个隐含位.(此处有一个点.),从而尾数值可能是0.0110,也可能是1.0110。E关系到规格化和非规格化。

双精度浮点数为64位:
对应于C语言中的double。
4、规格化
当指数位E表示的二进制序列不全0也不全1时,该浮点数为规格化形式。此时,指数位对应的实际值e被解释为表示偏置(bias)形式的整数,相应的计算公式为:
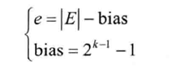
| E |表示E的二进制序列表示的整数值;bias为偏移量;k为指数位宽度,对于单精度而言,k=8,故bias=127,E=10000001(binary)时,| E |=129(decimal),所以e=129-127=2。
对于规格化浮点数,IEEE—754标准规定尾数位小数点左侧的隐含位位1,此时m的计算公式为:
m=| 1.M |
M=“1001000….0”,1.M=1.1001000…0,带入上式得到 m=1+2^(-1)+2^(-4)=1.5625。
所以:
n=(-1)^(0) x (1.5625)^(2)= 2.44140625
5、单精度规格化浮点数特点
(1)、由于E表示的二进制序列几部全为0也不全为1,所以E的表示范围为0~255.
(2)、尾数m的最小值为1,对应的M全为0,最大值为2-2^(-23)
(3)、规格化浮点数能表示的数绝对值最大值为(2-2^(-23))x 2^(127)。
单精度规格化浮点数计算公式为: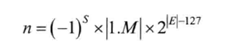
6、非规格化
当E的二进制位全部为0时,该浮点数为非规格化形式。指数位e和m为:

单精度非规格化浮点数计算公式为:
