Coursera《machine learning》--（6）逻辑回归

六 逻辑回归(Logistic Regression：LR)

逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就是由于这个逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。

6.1 分类问题（Classification）

本小节开始介绍分类问题（该问题中要预测的变量y是离散值），同时，还要学习一种叫做逻辑回归的算法（Logistic regression），这是目前使用最广泛的一种算法。虽然该算法中有"回归"二字，但其实它并不是一种回归算法，而是一种分类算法，只是由于各种历史原因才这么叫，不要纠结于这个问题。

6.1.1 什么是分类问题

什么是分类问题呢？下侧左图给出了一些分类问题的例子，分别为：垃圾邮件的分类问题、网上交易是否为诈骗的分类问题、肿瘤的分类问题等，在所有这些分类问题中，输出变量都是一个离散的值：0或1，其中，0为负类，1为正类（通常是这样使用的，但0和1到底哪个对应正类、哪个对应负类是任意的），也就是说，这些都是两类分类问题。另外，下图还给出了一个四类分类问题的情况，此时，输出变量也是一个离散值，但是取0、1、2、3中的某一个数。本小节主要讨论两类分类问题，也就是输出只有0和1的分类问题，在后面的章节中再讨论多类分类问题（多离散输出问题）。

那么，要如何开发一个分类算法呢？下面举一个例子，如上侧右图所示，给出了一个训练样本集，X为数据点（即肿瘤的大小），Y为观测值（即表示是否为恶性肿瘤），问题的目的是对肿瘤进行分类：恶性的还是良性的，输出只有两个离散值0和1。那么，应该如何解决这个分类问题呢？

6.1.2 线性回归可以解决分类问题吗？

实际上，线性回归方法并不能很好地解决分类问题。下面，尝试用线性回归方法进行分类；首先，利用训练集训练线性回归模型，也就是，尝试利用一条直线来拟合该训练样本集，可以得到下侧左图所示的假设函数h_θ (x)；然后，对于某一个待待分类样本，利用由训练样本集构建线性回归模型，判断它的类别，具体地：①对于该待测样本x，计算假设函数的取值h_θ (x)；②如果h_θ (x)≥0.5，则判断为恶性（正性）；如果h_θ (x)<0.5，则判断为良性（负性）。

换一种描述方式，如下侧右图所示，绘制y=0.5这条直线，与假设函数直线相交于点A，过点A作平行于y轴的直线x=x_A；对于某个给定的肿瘤大小，如果它位于位于x=x_A左侧，则为良性的，如果位于x=x_A的右侧，则为恶性的。

对于该例子而言，似乎这个假设函数可以正确区分训练样本集中的所有样本。但实际上，线性回归的鲁棒性是很差的。现对上图所示的训练样本进行一点小小的改造：如下图所示，在训练样本中添加一个尺寸非常大的恶性肿瘤（三角圈出的样本点），利用该训练集拟合出假设函数h_θ (x)，利用该模型对训练样本集中的样本进行分类，可以看到，出现了两个错分样本。因此，利用线性回归来解决分类问题并不是一个好的"主意"，可能有些比较"幸运"的情况才会出现还不错的结果。

有一个值得注意的问题：对于分类问题，它的输出y有两个取值：0或者1，如果我们利用线性回归算法来解决分类问题，得到的假设函数输出值可能远大于1或者远小于0（即使是在所有的训练样本的y值都等于0或者都等于1的情况）。所以，接下来要开始研究逻辑回归问题，该算法的特点是：它的输出永远是[0, 1]之间的数。

6.2 假设函数的表达

6.2.1 假设函数的形式

首先，讨论逻辑回归问题中的假设函数的表达形式（也就是说，在分类问题中，应该用什么样的函数来表示假设）。在上一小节中提到过，逻辑回归的假设函数的输出值位于[0, 1]之间，所以，我们需要找到一个满足这个性质的假设函数。

在线性回归问题中，假设函数具有如下形式：

    

在逻辑回归问题中，将该函数的形式转换为如下形式：

    

其中，函数g称为S型函数（sigmoid function）或者是逻辑函数（Logistic function）（这两个术语是可以互换的），它具有如下形式：

    

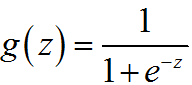
该函数图形如下图所示：

可以看到，S型函数的取值位于（0,1）之间，满足。那么，逻辑回归的假设函数的形式即为：

    

注意线性回归的假设函数和逻辑回归假设函数的形式上的区别：

线性回归假设函数为：

逻辑回归假设函数为：

6.2.2 假设函数的输出的意义

下面，讨论逻辑回归假设函数的输出的意义。

对于某个样本x，它对应的假设函数的输出值为h_θ(x)，该值表示样本x被判别为类为1的概率。

举一个具体的例子（肿瘤良性恶性的分类问题）：对于某个待测试样本x，它的假设函数的输出值h_θ(x)=0.7，该值表示：该样本为恶性肿瘤的可能性为70%。

接下来，再从条件概率的角度理解逻辑回归假设函数{h_θ(x)=P(y=1|x;θ)}的意义：在给定的样本x和参数向量θ的情况下，样本x被判断为类1的概率；那么，在给定的样本x和参数向量θ的情况下，输入样本x被判断为类0的概率为h_θ(x)=P(y=0|x;θ)：

6.3 判定边界

6.3.1 什么是判定边界

本小节主要介绍Decision Boundary的概念，它可以帮助我们理解逻辑回归的假设函数到底在计算什么。首先，讨论在什么情况下，假设函数的输出≥0.5。下图给出了sigmoid函数曲线（S型曲线），从左图可以看到：对于样本类别的判断完全取决于sigmoid函数的输出，而该输出又与函数自变量z具有直接关系，也就是说：

这里的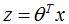，那么上式其实就是：

也就是说，对于给定的样本x，对于它的类别判断最终可由下式确定：

这里的所描述的曲线就是判定边界。注意到，利用判定边界和假设函数进行判断是等价的，只不过是与不同的数值比较大小。

6.3.2 如何利用判定边界

那么，如何利用判定边界进行分类预测？关于假设函数中的参数θ，这里先认为它是已知的，具体的计算方法会在后面的课程中讲述。

首先，看一个较为简单的例子。下图给出了一个训练样本集（+表示正样本，o表示负样本），每个样本的特征是二维的，它对应的逻辑回归函数为：，假设已经利用某种方法计算得到了参数向量θ=[-3,1,1]^T，那么，该问题的判定边界方程即为。对于一个待分类样本x=[x₁,x₂]，便可利用该判定边界对其进行分类，它的类别y计算方式如下：

接下来，看一个更加复杂的例子，下图给出了一个训练样本集（+表示正样本，o表示负样本），每个样本的特征仍是二维的，那么如何利用逻辑回归进行分类呢？对于逻辑回归问题，有时为了更好地得到分类边界，可以"添加额外变量"，所以，这里添加两个额外变量，假设该问题的假设函数h_θ(x)具有如下的形式：

    

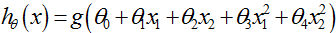
可以看到，在给定的3个特征基础上（x₀=1，x₁和x₂），又添加两个额外的特征。假设我们已经求得了参数向量θ=[-1 0 0 1 1]^T，则该最优参数对应的判定边界方程为，它是一个圆形的边界，其图像如下图所示，从而，决策规则为：。

还可以得到更加复杂的决策边界，例如下面给出的例子。

6.4 成本函数Cost和代价函数J

本小节主要介绍构造逻辑回归问题的成本函数Cost和代价函数J。如下图所示，给定了一个含有m个样本的训练样本集，每个样本具有n维特征，另外，为了计算方便，增加新的特征x₀=1，则每个样本有n+1个特征。x⁽ⁱ⁾为第i个样本的特征向量，y⁽ⁱ⁾为第i个样本的分类标签，回归问题的假设函数为h_θ(x)，那么，如何能够根据给定的训练样本集得到假设函数中的参数向量θ（也就是模型参数）呢？

参考线性回归分析中的代价函数J(θ)：

    

可以构造如下的代价函数J(θ)：

    

其中成本函数Cost为（类比线性回归问题构造的）：

    

但是，这个成本函数Cost是关于θ的非凸函数，它的图形如下图左侧所示，梯度下降法不能保证该函数收敛到全局最小值，但梯度下降法可以保证凸函数（如下图右侧所示）收敛到全局最小解。所以，我们需要寻找另外的代价函数，使它是凸函数。

对于逻辑回归问题，构造如下式所示的成本函数：

也就是说，当样本标签为1时，利用-log(h_θ(x))计算成本函数，该函数图像如下图左侧所示；当样本标签为0时，利用-log(1-h_θ(x))计算成本函数，该函数图像如下图右侧所示。

从图中可以看出成本函数的意义：

当y=1（即标签为1）时

1. 假设函数的输出值为1，则成本函数取值为0（实现了正确的分类，不需要付出代价）。
2. 假设函数的输出值为0，则成本函数取值为无穷大（分类错误，付出了无穷大的代价）。

注：为什么逻辑回归的成本函数可以写为这种log的形式？

6.5 简化的成本函数和梯度下降

本小节主要讲解如何简化成本函数的写法，同时，介绍如何利用梯度下降法来解决逻辑回归中的参数求解问题。

6.5.1 简化的成本函数和代价函数

下式给出了逻辑回归问题的代价函数J(θ)（即考虑了m个训练样本）：

    

可以看到，在分类问题中，训练样本的y值永远是1或者0，所以可以据此来简化成本函数的书写（即将原来的分情况讨论的两个式子合并为一个式子），简化后的成本函数如下：

从而，逻辑回归的代价函数J(θ)可以写为：

    

通过最小化代价函数J(θ)可以得到最优的向量参数：。

在得到逻辑回归问题的最优化向量参数后：

可以利用假设函数对待预测样本x进行分类：（其中）

也可以利用判别边界对该待测样本x进行分类：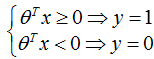

6.5.2 逻辑回归问题的梯度下降法

那么，如何通过最小化逻辑回归问题的代价函数求得最优的参数呢？下图给出了利用梯度下降法（Gradient Descent）求解逻辑回归问题具体的流程：左侧是梯度下降法，右侧是将梯度下降法应用于逻辑回归。

其中：

优化问题的关键问题是代价函数相对于待优化参数的梯度和代价函数取值的求解，所以，实际中，需要首先编写一个计算代价函数和代价函数梯度的函数，例如，在matlab中实现，需要编写costFunction函数，该函数根据输入的训练样本集及其相应的标签，计算在输入的当前参数向量值下，代价函数的取值及在当前参数向量下的偏导数（已经向量化）：

1. 利用下式计算代价函数取值

   

2. 利用下式计算代价函数的偏导数

   

*****偏导数公式的推导过程*****

*****向量化的推导过程*****

6.6 高级优化

本小节将介绍一些高级算法，使得梯度下降法的速度大幅度的提升，从而，可以将梯度下降法适用于大型的机器学习问题。现在，我们换个角度来看一下什么是梯度下降法，有一个代价函数J，优化的目标是最小化J，程序的要做的事情是，当输入参数向量θ时，可以输出J(θ)和J对各参数的偏导数。可以实现这一过程的代码如下图所示：

根据代码可以看出，梯度下降法的目的就是要计算J(θ)和J对各参数的偏导数，然后，将它们插入到迭代算法中，就可以一步步地最小化代价函数。在梯度下降算法中，其实不需要计算代价函数，只要计算代价函数对各参数的偏导数即可，但有时为了监控程序的运行过程，可以计算代价函数的取值。同时，梯度下降算法并不是唯一可以使用的方法，还有一些更高级、更复杂的方法，例如Conjugate gradient、BFGS和L-BFGS等，下图给出了它们的优缺点（其实，具体使用时，可以不知道这些算法那的具体原理）。

下面，举例说明如何使用这些优化算法，现在，有一个两参数优化问题：

可以利用不同的优化算法计算得到最优参数向量，具体地：

（1）构造函数costFunction，它的作用是计算J(θ)和J对各参数的偏导数；

（2）利用matlab自带函数optimset、fminunc得到最优化的参数向量

6.7 多类分类：一个对所有

本节主要讨论如何将逻辑回归应用到多类分类问题中，通过一个叫做"一对多"的分类算法。下图给出了一些多类分类问题。

如下图所示，左侧是一个二元分类问题的训练样本集，右侧是一个三元分类问题的训练样本集。那么，如何得到一个学习方法呢？利用一对多的分类思想，可以将逻辑回归应用到多元分类问题上。

下面，介绍如何利用一对多的思想进行分类。如下图所示，左侧给出了一个具有三类样本的训练集，要对这三类样本进行分类，那么，利用两类问题的回归分析方法，可以将这个三元分类问题转化为三个二元分类问题。将具有N类样本训练样本集分为N个伪训练集，对于第i个伪训练集，认为类别为i的样本为一类，其余所有的样本为另一类，这样，可以利用两类分类问题的逻辑回归方法对该伪训练集求解决策边界，这样，利用N个伪训练集可以得到N个决策边界（也就是N个假设函数）。

如上所述，利用N个伪训练集可以得到N个决策边界（也就是N个假设函数），那么对于一个待分类样本x，可以利用如下的方法预测它属于哪一类：将该样本x分别代入N个假设函数中，计算得到N个假设函数的输出值，哪个输出值最大，就将x判别属于该最大值对应的假设函数对应的类别。