本笔记为Coursera在线课程《Machine Learning》中的神经网络章节的笔记。
八、神经网络:表述(Neural Networks: Representation)
本节主要讨论一种叫做神经网络的机器学习算法。首先讨论神经网络的表层结构,在后续的课程中再讨论具体的学习算法。神经网络其实是一个比较古老的算法,它沉寂过一点时间,但现在又成为了许多机器学习的首选技术。
8.1 非线性假设
参考视频: 8 - 1 - Non-linear Hypotheses (10 min).mkv
前面已经讲述了线性回归和逻辑回归算法,为什么还要研究神经网络呢?下面,通过几个机器学习的例子来阐述研究神经网络的目的,这几个例子的解决都依赖于复杂的非线性分类器。
考虑下图所示的监督学习的例子(房价分类问题,而不是不是以前的房价预测问题,给定房子的一些特征,预测在未来半年内该房子是否可以卖得出去,这是一个分类问题),在图中,给出了训练样本集(其中,+为这个样本,-为负样本)。如果利用逻辑回归来解决这个问题,首先需要构造一个包含很多个非线性项的假设逻辑回归函数(包含很多的二次项、甚至三次项等);当非线性项足够多时,可以得到能够将正样本和负样本区分开的分类边界(如下图的分类界面所示)。当只有两个特征时(x1和x2),这种分类方法的效果其实还是不错的,因为可以将x1和x2的所有组合都包含在多项式中。

但对于许多复杂的机器学习问题,涉及到的特征往往多于两项,例如,某个房子可能有100个特征(即n=100),此时,如果仍旧利用逻辑回归方法,即使在逻辑回归函数中仅考虑所有的二次项,那么最后的回归函数也会有5000个二次项:

并且,随着特征特殊个数n的增加,二次项的个数大约以n2的量级增长(计算复杂度是o(n2),二次项的个数大约是n2/2个),所以说,要在逻辑回归函数中包含所有的二次项是非常困难的,更不要说再包含三次项、四次项等(如果考虑三次项,计算复杂度将会变为o(n3)),回归函数大概包括17000个三次项)。并且,由于多项式项个数的增加,最后结果可能会产生过拟合的问题,同时,处理这么多的项,也会存在运算量过大的问题。同时,如果真的只考虑二次项,也会抛弃大量的其他特征,使得最后得到的决策边界并不好。实际中,许多机器学习问题的特征个数n是很大的,以下给出一些例子。
下图给出了一个计算机视觉中的问题:利用机器学习来训练一个分类器,它可以判定一副输入图像是否为一辆汽车。取出图像中的一个小矩形部分,将其放大,可以看到,人类眼中的汽车,计算机看到的却是一个数值矩阵(每个数值代表相应位置的灰度值),所以,这个识别问题对计算机而言,就变为了根据像素点亮度矩阵判断这个数值矩阵到底代表的是什么。

具体而言,用机器学习算法构造汽车识别器的基本过程是:将给定的一个带有标签的样本集(其中,一类是汽车样本,另一类是非汽车样本)输入到学习算法中,从而得到一个分类器;对于给定的一个新的测试样本,该分类器就可以判断出"这是什么东西"。理想情况下,分类器可以识别出一个汽车。

为了描述引入非线性分类器的必要性,从训练样本集中挑出一些汽车图片和非汽车图片,从每组图像中挑出一组像素点(pixel1和pixel2两个像素点),在坐标系中标出该汽车的位置(即为坐标系中的一个点,x坐标为pixel1亮度值、y坐标为pixel2亮度值),利用同样的方法,标出其它图片中的汽车的位置及非汽车物体的位置,绘制结果如下图所示。对于这种简答的情况,似乎结果还是可以线性分割的。
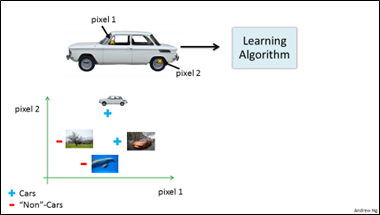
下面,继续绘制更多的样本点,绘制结果如下图所示。可以看到,汽车样本和非汽车样本分布在坐标系中的不同区域(一个非线性分类问题),所以,我们需要一个非线性分类器将这两类样本尽量区分开来(下图绘制出了一个非线性的决策边界)。

这个分类问题的样本特征个数大概有多少呢?假使我们采用的样本像素大小都是50×50,并且将所有的像素点的灰度值视为特征,则会有 2500个特征,如果再进一步将两两特征组合构成一个多项式模型,则会有约25002/2 个(接近300万个)特征。因此,只是简单地增加二次型、三次项等的逻辑回归算法,并不是一个解决复杂非线性问题的好办法,因为当n值很大时,会产生非常多的特征项。所以,接下来,将要讲解神经网络算法,它被证实:在求解非线性分类问题中,即使在n值很大时,它是一种很好的算法。
8.2 神经元和大脑
参考视频: 8 - 2 - Neurons and the Brain (8 min).mkv
神经网络是一种很古老的算法,它最初产生的目的是制造能模拟大脑的机器。由于神经网络能够很好地解决不同的机器学习问题(而不只因为它们在逻辑上行得通),现在又重新被应用到各种实际问题中。本小节,主要讲述一些神经网络的背景知识,由此我们能知道可以用神经网络来做什么(可以将它应用到现代的机器学习问题上,或者是那些你可能会感兴趣的问题中)。也许,这一伟大的人工智能梦想在未来能制造出真正的智能机器。
神经网络产生的原因是人们想尝试设计出模仿大脑的算法:从某种意义上说,如果我们想要建立学习系统,那为什么不去模仿我们所认识的最神奇的学习机器-人类的大脑呢?神经网络逐渐兴起于二十世纪八九十年代,当时应用得非常广泛,但由于各种原因,在90年代的后期应用减少了。但是最近,神经网络又东山再起了,其中一个原因是:尽管神经网络是一个计算量有些偏大的算法,但近些年来计算机的运行速度变快,使得大规模的神经网络算法得以运行。正是由于这个原因和其他一些我们后面会讨论到的技术因素,如今的神经网络对于许多应用来说是最先进的技术。

我们能学习数学,学着做微积分,而且大脑能处理各种不同的令人惊奇的事情,似乎如果你想要模仿它,你得写很多不同的软件来模拟所有这些五花八门的奇妙的事情。不过,能不能假设大脑要做所有这些不同事情时,不需要用上千个不同的程序去实现,而只通过一个单一的学习算法就可以了?下面可以看一些这方面的证据。
如下面左图所示,大脑中的一小片红色区域是听觉皮层。耳朵接收到声音信号,并把声音信号传递给听觉皮层(这样,'你'才能明白'我'的话)。神经系统科学家做了个有趣的实验,把耳朵到听觉皮层的神经切断,在人眼和听觉皮层建立联系,这样,从眼睛到视神经的信号最终将传到听觉皮层。结果表明,听觉皮层将会学会"看"。下面再举另一个例子,如下面右图所示,这块红色的脑组织是躯体感觉皮层,它是用来处理触觉的,如果做一个和刚才类似的重接实验,那么躯体感觉皮层也能学会"看"。


这个实验和其它一些类似的实验,被称为神经重接实验,从这个意义上说,如果人体有同一块脑组织可以处理光、声或触觉信号,那么也许存在一种学习算法,可以同时处理视觉、听觉和触觉,而不是需要运行上千个不同的程序、或者上千个不同的算法来做这些大脑所完成的成千上万的美好事情。我们需要做的就是找出一些近似的或实际的大脑学习算法,然后使大脑通过自学掌握如何处理这些不同类型的数据。在很大的程度上,可以猜想如果我们把几乎任何一种传感器接入到大脑的几乎任何一个部位的话,大脑就会学会处理它。
下面再举几个例子。下图左侧是用舌头学会"看"的一个例子。这实际上是一个名为BrainPort的系统,它现在正在FDA (美国食品和药物管理局) 的临床试验阶段,它能帮助失明人士看见事物。它的原理是:你在前额上带一个灰度摄像头,面朝前,它就能获取你面前事物的低分辨率的灰度图像。你连一根线到舌头上安装的电极阵列上,那么每个像素都被映射到你舌头的某个位置上,可能电压值高的点对应一个暗像素电压值低的点。对应于亮像素,即使依靠它现在的功能,使用这种系统就能让你我在几十分钟里就学会用我们的舌头"看"东西。


上图右侧是第二个例子:人体回声定位或者说人体声纳。你有两种方法可以实现:你可以弹响指,或者咂舌头。不过现在有失明人士,确实在学校里接受这样的培训,并学会解读从环境反弹回来的声波模式—这就是声纳。如果你搜索YouTube之后,就会发现有些视频讲述了一个令人称奇的孩子,他因为癌症眼球惨遭移除,虽然失去了眼球,但是通过打响指,他可以四处走动而不撞到任何东西,他能滑滑板,他可以将篮球投入篮框中。
第三个例子是触觉皮带,如下图左侧所示,如果你把它戴在腰上,蜂鸣器会响,而且总是朝向北时发出嗡嗡声。它可以使人拥有方向感,用类似于鸟类感知方向的方式。


还有一些离奇的例子:如果你在青蛙身上插入第三只眼(如上图右侧),青蛙也能学会使用那只眼睛。因此,这将会非常令人惊奇。如果你能把几乎任何传感器接入到大脑中,大脑的学习算法就能找出学习数据的方法,并处理这些数据。从某种意义上来说,如果我们能找出大脑的学习算法,然后在计算机上执行大脑学习算法或与之相似的算法,也许这将是我们向人工智能迈进做出的最好的尝试。人工智能的梦想就是:有一天能制造出真正的智能机器。
神经网络可能为我们打开一扇进入遥远的人工智能梦的窗户,但我在这节课中讲授神经网络的原因,主要是对于现代机器学习应用。它是最有效的技术方法。因此在接下来的一些课程中,我们将开始深入到神经网络的技术细节。
8.3 模型表示1
参考视频: 8 - 3 - Model Representation I (12 min).mkv
本节主要介绍如何表示神经网络,也就是说,当我们利用神经网络时,应该如何表示假设或者模型呢?神经网络是在模拟大脑中的神经元时发明的,所以,为了解释如何对假设进行表示,需要首先看看单个神经元在大脑中是什么样子。在我们的大脑中,充满了如下图左侧所示的神经元,每个神经元都有一个细胞核、一定数量的输入神经(树突Dendrite)、一个输出神经(轴突Axon)。简单来讲,神经元是一个计算单元,它从输入神经接收一定数目的信息,并作出一些计算,将计算结果通过轴突传送到其他神经元。


上图右侧是一组神经元的示意图,神经元利用微弱的电流进行沟通,这些弱电流也称作动作电位。如果神经元想要传递一个消息,它就会通过它的轴突发送一段微弱电流给其他神经元,这个神经元接收到这条信息,作出一些计算,再将计算的信息传送给其他的神经元。其实,这就是人类思考的模型:神经元把自己的收到的消息进行计算,并向其他神经元传递消息。这也是我们的感觉和肌肉的运转原理。例如,如果你想活动一块肌肉,就会触发一个神经元给你的肌肉发送脉冲,并引起你的肌肉收缩,如果一些感官(例如眼睛)想要给大脑传送一个消息,那么它也会这样发送电脉冲给大脑。
在一个神经网络中(或者说,我们在电脑上实现神经网络时),我们可以使用一个非常简单的模型来模拟神经元的工作。将神经元模拟为一个逻辑单元,如下图所示,中间的黄色圈圈可以看做类似于神经元的东西,然后通过它的树突(或者叫做它的输入神经input wires)传递给该神经元一些消息,接下来该神经元做一些计算,并通过它的轴突(或叫做输出神经output wires)输出计算结果。

该模型是一个及其简单的模拟神经元模型,它的三个输入为x1~x3,输出是类似于逻辑回归中的假设函数的形式hθ(x)。在绘制时,通常只绘制输入x1~ x3,但有时也会增加一个额外的节点x0,被称为"bias unit",由于x0总是等于1,所以,在本课中,有时会画出它,而有时不会。下面,再讨论一下关于神经网络的术语:对于上图给出的神经元,称它为一个以s型函数(逻辑函数)作为激励函数的人工神经元,在神经网络中,激励函数只是对类似于'非线性函数g(z)'的另一个术语称呼。θ称为模型的参数,在神经网络中,它更多地被称为模型的权重(模型的参数和模型的权重是相同的概念)。
什么是神经网络呢?下图给出了神经网络的例子,它其实就是很多的神经元组合在一起的集合。神经网络模型是许多逻辑单元按照不同层次组织起来的网络,每一层的输出变量都是下一层的输入变量。具体地:
(1)具有三个输入单元x1~x3,有时会画出一个额外的节点x0(偏执单元)(无论画出与否,计算时是肯定要考虑的);
(2)具有三个神经元 ,有时,会画出一个额外的偏置单元
,有时,会画出一个额外的偏置单元 ,它的输出永远是1。
,它的输出永远是1。
(3) Layer1为输入层(Input Layer),因为在该层输入了特征项x1~x3;Layer3为输出层(Output Layer),因为该层计算得到了输出值;中间的一层称为隐藏层(Hidden Layers),在监督学习中,可以看到输入层和输入层,看不到中间层,所以才称中间层为隐藏层。为每一层都增加一个偏差单位(bias unit))

下面,解释一些记号,用来描述模型:
(1):第j层的第i个神经元,即:上标i代表第几层,下标j代表第几个神经元。例如:表示第二层的第1个激励(即隐藏层的第一个激励,所谓激励,是指由一个神经元读入、计算并输出的值)。
(2)Θ(j):从第j层映射到第j+1层时的权重的矩阵。例如Θ(1)表示从第一层映射到第二层的权重的矩阵,其尺寸为:以第j+1层的激活单元数量为行数,以第j层的激活单元数+1为列数的矩阵。例如:上图所示的神经网络中Θ(1)的尺寸为 3*4。(这里的提到的激励单元数不包括偏执单元)


接下来,看一下这个神经网络展现了什么样的计算呢?仍旧以前面的神经网络为例,它有三个input units和三个hidden units。

该网络隐藏层的输出为:

最后的输出为:

注:
8.4 模型表示2
参考视频: 8 - 4 - Model Representation II (12 min).mkv
本小节主要讲述如何利用向量化的方法描述神经网络的计算。以下面的神经网络为例。

对于第一层到第二层有:

写为矩阵形式为:
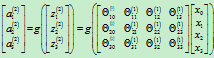 ,即:
,即: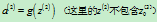
其中:
 ,即
,即 ,
,
解释一些符号:
 :第j层的第i个神经元的输入;
:第j层的第i个神经元的输入; :列向量,为第j层所有神经元的输入
:列向量,为第j层所有神经元的输入
 :第j层的第i个神经元的输出;
:第j层的第i个神经元的输出; :列向量,第j层所有神经元的输出
:列向量,第j层所有神经元的输出
注意到,以上只是针对一个训练集,如果有N个训练集,即网络的输入为:

那么,对整个训练集进行计算时:
 ,即
,即 ,而
,而  。
。
这里的 ,每一列分别为某一个输入训练样本的第二层激励的所有输入(不包括偏执单元)。
,每一列分别为某一个输入训练样本的第二层激励的所有输入(不包括偏执单元)。
接下来,为了更好了了解Neuron Networks的工作原理,我们先把左半部分遮住:剩下的部分很像是逻辑回归(如下图所示),利用逻辑回顾单元来预测hΘ(x)的输出。

其实神经网络就像是logistic regression,只不过把logistic regression中的输入向量[x0~x3]变成了中间层的 ,即:
,即:
注:可以把a0,a1,a2,a3看成更为高级的特征值,也就是x0, x1, x2, x3的进化体,并且它们是由x与θ决定的,因为θ是梯度下降的,所以a是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将x次方厉害,也能更好的预测新数据。这就是神经网络相比于逻辑回归和线性回归的优势。
8.5 特征和直观理解1
参考视频: 8 - 5 - Examples and Intuitions I (7 min).mkv
首先,给出一些常用的逻辑运算:OR(或运算)、AND(与运算)、XOR(亦或运算,不同为1)、XNOR同或运算(也成为亦或非,相同为1)。
本小节给出一个例子,说明神经网络是如何学习复杂非线性假设的。首先,以一个简单的AND运算为例,功能要求:输入x1和x2都是二进制,输出y=x1 AND x2(逻辑与运算)。

下面的神经网络实现了或运算(OR)。(也是用单层神经元)

从本质上讲,神经网络能够通过学习得出其自身的一系列特征。在普通的逻辑回归中,我们被限制为使用数据中的原始特征x1,x2,...,xn,我们虽然可以使用一些二项式项来组合这些特征,但是我们仍然受到这些原始特征的限制。在神经网络中,原始特征只是输入层,在我们上面三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
8.6 样本和直观理解II
参考视频: 8 - 6 - Examples and Intuitions II (10 min).mkv
上一小节讲解了如何利用神经网路来计算x1和x2的与运算和或运算,其中:x1和x2都是二进制数。本小节,首先给出一个非运算的例子。总体思路:想要计算非运算,在取非运算的变量前面加上一个绝对值大的负数作为权值;

接下来,再看一个非x1与非x2的例子,可以在x1和x2的前面放一个绝对值大的负数作为权值,也可以通过建立一个神经网络来进行计算。

有了以上一些简单的逻辑运算,就可以计算XNOR(同或)运算了:将与运算、非与非运算和或运算组合在一起,结果如下图所示:

8.7 多类分类
参考视频: 8 - 7 - Multiclass Classification (4 min).mkv
当我们有不止两种分类时(也就是y=1,2,3….),比如以下这种情况,该怎么办?如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层我们应该有4个值。例如,第一个值为1或0用于预测是否是行人,第二个值用于判断是否为汽车,第三个值用来判别是否为摩托车,第四个值用来判别是否为truck。输入向量x有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现[a b c d]T,且a,b,c,d中仅有一个为1,表示当前类。下面是该神经网络的可能结构示例:
