首先,Shell是发明这个算法的人名,不是这个算法的思想或者特点。
希尔排序,也称为增量递减排序。基本思路,是把原来的序列,等效视为一个矩阵的形式。矩阵的列数,也称为宽度或者增量,记为w。
假设数组A[n]以及矩阵B[][],对于两者的对应关系,可以记为A[k]=B[k/w][k%w]。也就是说,A中的元素会按照先行后列的顺序排列,即先左后右、先上后下的顺序放入矩阵B中。
对于增量或者说矩阵的宽度w,会有许多策略进行选择。假设w={1,2,4,8,16,32...}。从w的集合中选择小于数组元素数量n的最大元素w[i],并且选取w[0]到w[i]之间的所有增量,从w[i]开始,按照矩阵B中的每一列进行排序。这里的排序必须是输入敏感的,通常采用插入排序。本次完成后,取下一个w,再按照每列进行排序。直到w=1,矩阵退化为向量,排序完成。
1 int max(int* H, int n, int size) 2 { 3 int i = 0; 4 while (i < n&&size > H[i]) i++; 5 return i - 1; 6 } 7 void shellSort(int* A, int lo, int hi)//[lo,hi) 8 { 9 int H[11] = { 1,5,19,41,109,209,505,929,2161,3905,8929 }; 10 int size = hi - lo; 11 int gap = max(H,11,size);//选取小于规模的最大增量 12 for (int t = gap; t >= 0; t--)//从W[gap]一直到w=1,递减增量 13 { 14 int w = H[t];//选取步长,w即增量也是宽度(列数) 1516 for (int k = 0; k < w; k++)//对于每一列 17 { 18 for (int i = lo + w; i < hi; i += w)//下面的循环即插入排序 19 { 20 int j = i - w; 21 int tmp = A[i]; 22 while ((j >= lo) && (A[j] > tmp)) 23 { 24 A[j + w] = A[j]; 25 j -= w; 26 } 27 A[j + w] = tmp; 28 }//一列的插入排序结束 29 }//每列都进行插入排序 30 } 31 }
希尔排序的总体策略,就是通过按列排序,使得每次排序后的局部有序性增加,最后达到全序列排序的目的。具体的证明可以参考《数据结构C++语言版》,有比较详细的h-有序和(g,h)-有序以及有序性增加的介绍。
下面是一个n=12,w{1,5}的过程。可以看到,w=5排序过后,有序性确实会有一定增加。
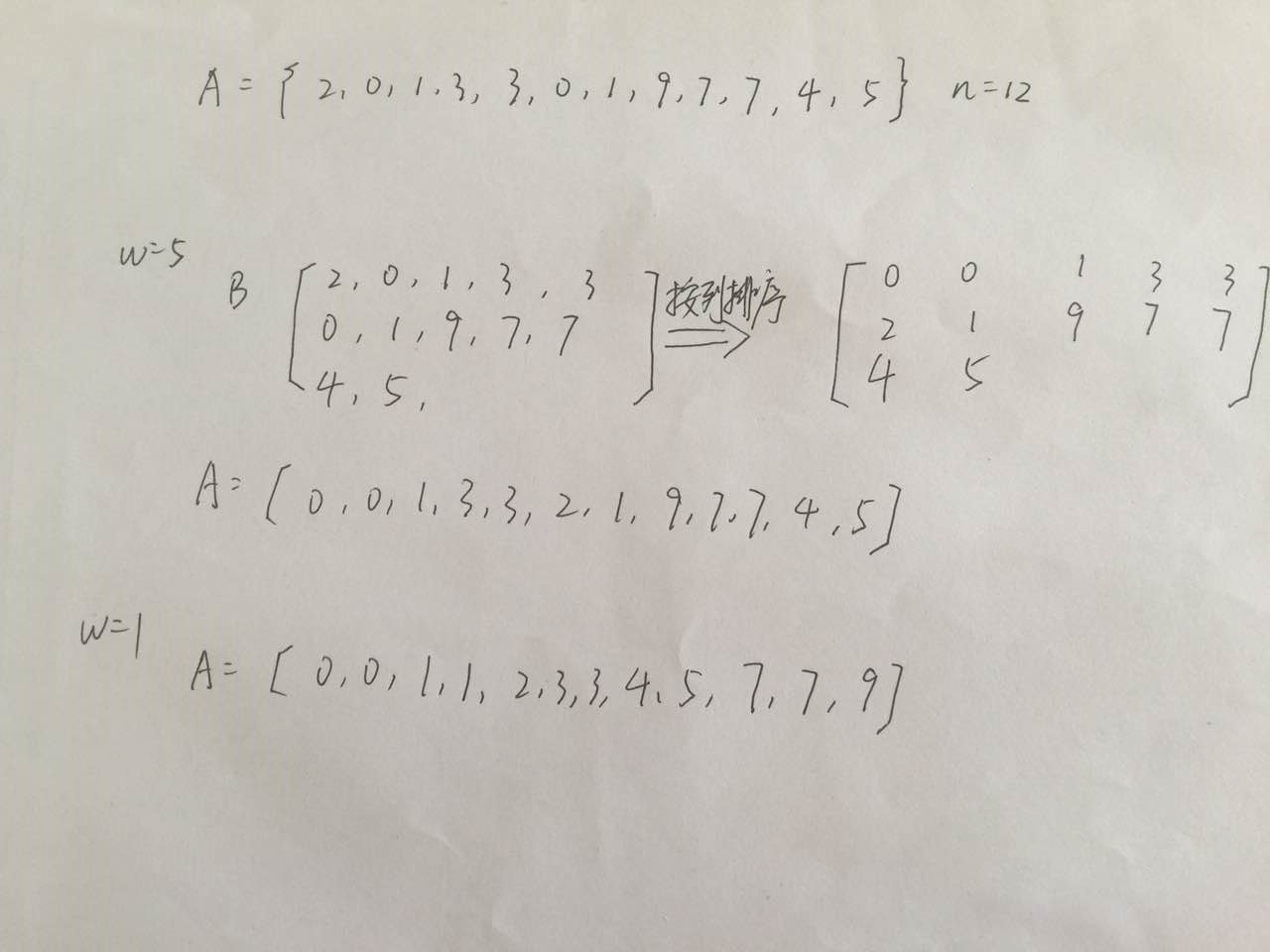
希尔排序的复杂度,取决于增量序列w的选择。几个比较优秀的序列,Pratt序列{1,2,3,4,6,8,9,12,..2^p*3^q,...}。这个序列的缺点很明显,会造成排序迭代次数很多,不过时间复杂度可以达到O(nlog^2n)。Sedgewick序列{1,5,19,41,109,209,505,929,2161,3905,8929...}的时间扶再度在最坏情况下可以为O(n^(4/3)),最好情况下为O(n^(7/6).