链接: https://leetcode.com/problems/trapping-rain-water/
【描述】
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
For example,
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.
【中文描述】
给定n个非负数,想像它们代表了n堵墙,墙的高度就是Ni, 现在想像下了一场雨,让求这些墙能保存多少水?如图:

————————————————————————————————————————————————————————————
【初始思路】
这个题挺有意思, 所以也没看discuss, 完全自己硬刚出来的。这个题其实不难,主要是考验思维的缜密程度,然后逐段逐情况分析即可。
我一开始的思路是(brutle的就不讨论了吧),用i遍历数组,遇到比i高的,就停下来,然后算里面的水量,然后更新i。
这是最基本的思路了,但是,里面有巨量的细节需要考虑:
细节1: 如果i下一位比i高或和i一样高,显然i这堵墙就没用了, continue;
好了,i 的下一堵墙肯定低于 i 墙,这个时候,我使用了动态规划的思想,不管三七二十一,先开始按照 i 墙的高度算水量,给一个变量j = i+1, j一直移动到结尾。
那么在 j 移动到结尾的过程中,有几种可能性:
(1)遇到了某一堵墙比 i 墙要高, 真是太好了, 那么计算到这个位置的时候, 这段区间内的水量就是咱们动态规划计算出来的水量, result加入这个值就可以了。然后j也不用再往后看了, i=j,continue即可, 可以看下图帮助理解这种情况, 浅绿色的面积 == maxPoten, 这就是留水量。这个值加入result后, i移动到j,然后继续用j往后找就行了。
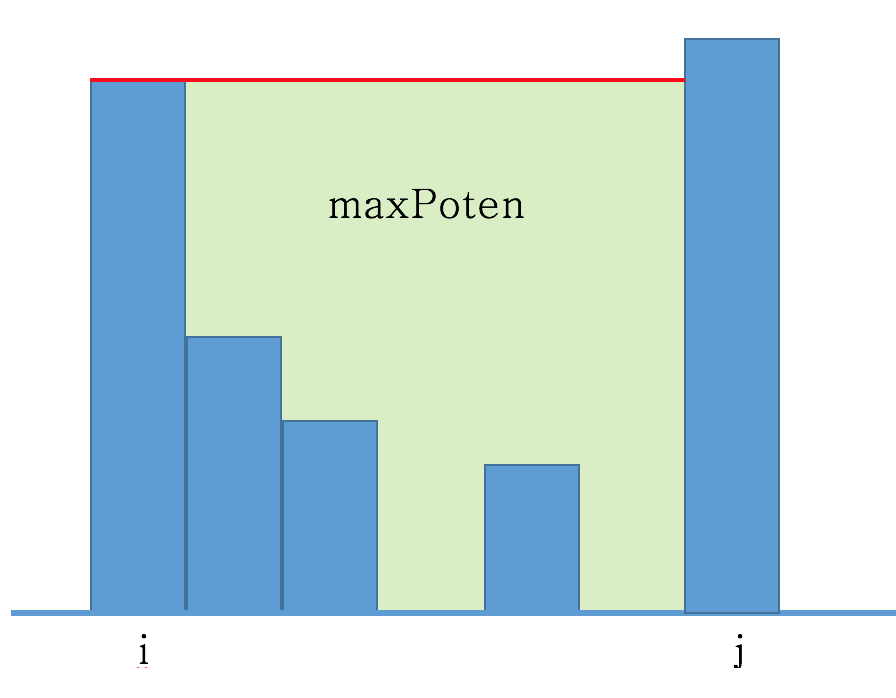
(2)从头到尾,j都没有遇到比i还高的墙,那怎么办?这个时候,最简单的办法是,i 直接continue。 但是,这样的话,我们刚才算过的值全都白算了,而且这样算,时间复杂度肯定就接近O(n2)了。所以我根本没实现这个思路(虽然这个思路是最简单的,面试时候可以直接这么写);
(2改)我的思路是,已经算的不能白费,怎么办呢?既然比 i 墙高或者等于 i 墙的没找到,那我们就争取找到比 i 低的最远处的一堵墙。如果最坏情况下,没找到比 i 墙高或者等于 i 墙的, 我们还可以用比 i 墙稍低一点的这个墙来补偿,刚才做的计算也不会白费。 并且!!最重要的是, 这样计算完后, i可以直接跳到这堵稍低点的墙的位置,时间复杂度大大降低。最优情况可以接近O(n)!
好了, 这样的话,我们在计算j->结尾的这个过程中, 有几个变量需要实时计算:
maxPoten, 代表了最大可能留水量。当找到比i墙高或者等于i墙的, 这个值就是留水量, 绝对不会错!
lower, 代表了没找到理想墙,但是找到了比 i 墙稍低一点的墙, 那么在这种情况下, lower墙决定的留水量就是这个区间内的留水量,绝对不会错!
lowerPoten,代表由lower墙决定的留水量。 并且,lowerPoten和maxPoten之间有算术关系,稍后我们讨论这个关系,并且给出公式。
这些是否足够了?我们来看看下面的图,帮助理解这种情况下可能的问题:
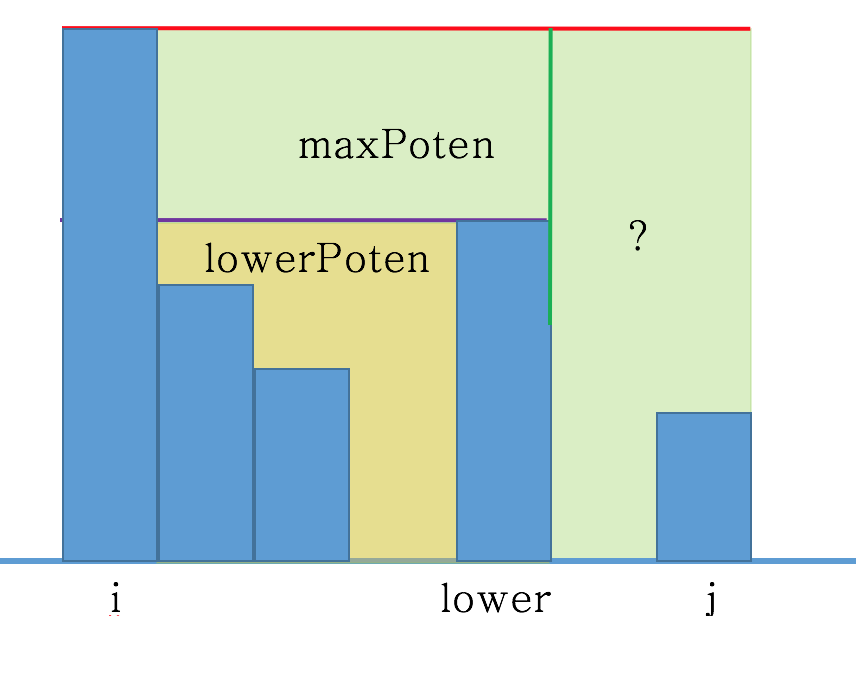
如上图, 找到lower后,实际的存水量应该是lowerPoten,那么lowerPoten怎么算出来。maxPoten -(两墙高差)*(两墙距离) = lowerPoten?光凭抽象理解,很容易得出这样一个错误的式子,但是看上面图就一目了然了, 细节2: lower后面的面积,也需要减去!正如图上标示的一样,这个面积怎么算?
我们根据lower的更新机制来看, 这个面积其实和lower息息相关,我们实时计算的时候,除了实时计算maxPoten,再计算这个面积,然后每次求出新的lower的时候,这个面积归零。最终,我们就可以求得这个面积了。
所以,我们还需要一个变量: lowerBehind.
那么, lowerPoten = maxPoten - lowerBehind - (两墙高差)*(两墙距离)。
这样是否就OK了?答案是否定的,我们来看下面的图:
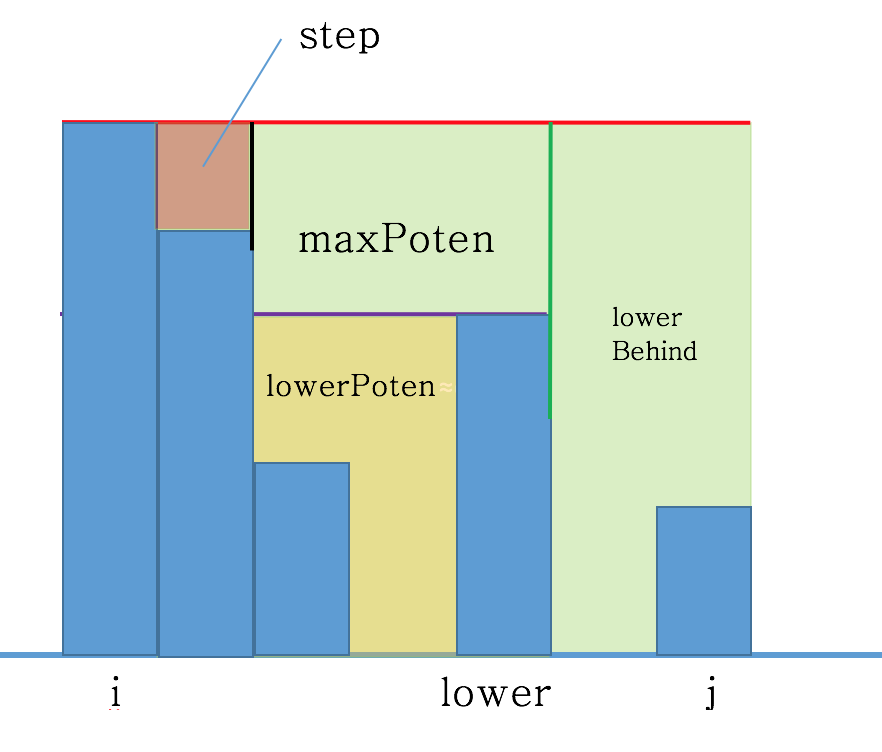
上图可以很明显看出来, 由于左上角橘红色区块的存在,之前的公式就是错误的了: lowerPoten = maxPoten - lowerBehind - (两墙高差)*(两墙距离)。
因为显然,细节3: maxPoten需要减掉step上的水体积,然后再减(lower和step之间的间距) * (两墙高差) 才能得到正确答案。
所以,需要考虑下怎么算step上的水量。
思考一下step为何会产生,从图上可以看出来,因为step高度>=lower墙的高度。step的确定看似简单:j从i+1位开始往后推移的时候,遇到比lower高且和i墙紧邻的都是step。但是实现的时候这个想法就不好实现了,因为lower还没有产生,我怎么知道当前这个墙是不是step。 所以,我的思路是:
只要 j 墙紧邻 i 墙,就把 j 墙先算作step,然后存入一个list里。
怎么确定紧邻?简单,给一个boolean的紧邻标记=true, 只要当前 j 墙不为0且紧邻标记为true,那么当前 j 墙肯定紧邻 i 墙。如果一旦 j 墙==0了,紧邻标志置为false即可。
在最终确定了lower后,我们再遍历这个list,把从左往右最后一个大于lower的墙标记为最右step墙。 那么 step1, step2, .. stepn的水量加起来就是上图中的step水量。同时,因为已经算出了最靠右的step墙,那么lower和这个墙之间的差距就可以用来算lowerPoten了。
到此,我们得出最后的公式:
lowerPoten = maxPoten - lowerBehind - stepWater -(两墙高差)*(lower - 最右step墙)
最后整个算法最核心的点:lower,怎么算?
首先,lower肯定是从最小往最大去更新。 那么lower最开始=0, 然后遇到比当前lower大的,lower就更新。但是这样做的话,有一种情况就无法解决了。看下图:
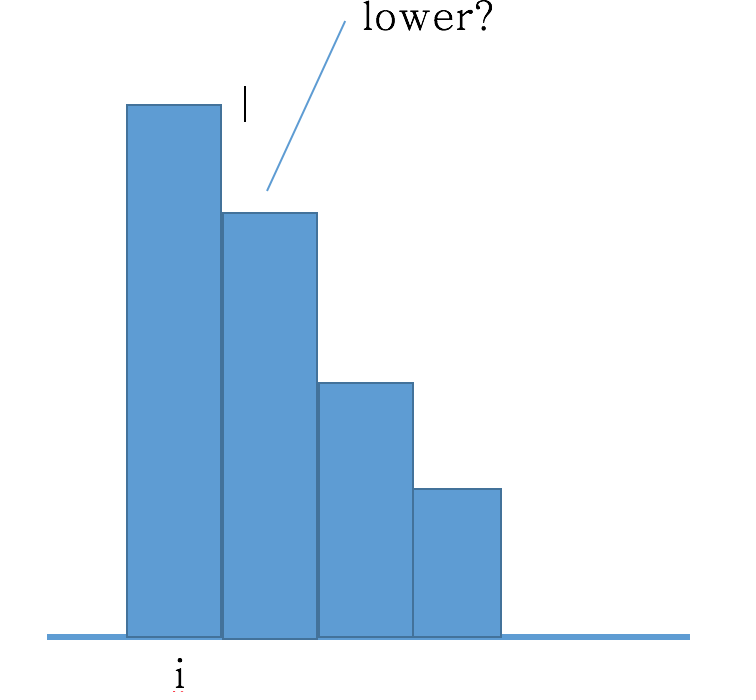
根据上面描述,那么遇到这种递减数列到结束的情况, lower就会在i + 1的位置。这显然是不合理的。因为这样的话,这种情况下也能留水!那么lower应该怎么选?
显然,lower只要在数列不是递减的情况下,才会至少找到一个。如果数列递减,lower肯定不能找到。
所以,lower的更新机制,除了上面提到的之外,还需要加上,细节4: j 墙 > j - 1墙的情况下, lower开始更新。一旦出现了j墙>j-1墙的情况, 肯定不是递减数列了,那么就可以更新lower了。
到此,整个算法里的细节就都分析到了,综上,可以写出代码。
【Show me the Code!!!】

1 if (height == null || height.length == 0) return 0; 2 3 int result = 0; 4 int i = 0; 5 while (i < height.length) { 6 //每次i移动后, 几个变量要归0 7 int maxPoten = 0; 8 int lowerPoten = 0; 9 int lower = -1; 10 int lowerBehind = 0;//lower后的总水量,必要时候要减掉,每次lower更新后,此值更新到0,并重新累积 11 if (i < height.length - 1 && height[i] <= height[i + 1]) { 12 i++; 13 continue;//当前i比后一个矮, 直接continue, 细节1 14 } 15 List<Integer> union = new ArrayList<Integer>();//保存和i墙连续的低墙 16 boolean isUnion = true; 17 int j = i + 1; 18 while (j < height.length) { 19 if (height[j] >= height[i]) { 20 //找到了比height[i]还高或者一样高的, 直接break; 21 //当前的maxPoten就是临时结果,直接加入result即可 22 break; 23 } 24 if (lower == -1 && height[j] > height[j - 1]) { 25 //第一次出现了升序, lower更新到第一个位置, 细节4 26 lower = j; 27 } 28 if (height[j] == 0) { 29 isUnion = false; 30 } 31 maxPoten += height[i] - height[j];//每一步都要计算maxPoten 32 lowerBehind += height[i] - height[j];//细节2, lower后的面积需要计算出来,必要时候要减去 33 if (isUnion) { 34 union.add(j);//最终计算的时候, union部分也需要考虑 35 } 36 if (lower != -1 && height[j] >= height[lower]) { 37 lower = j;//更新lower到最远,且高度仅次于height[i]的位置 38 //每次更新lower后,lowerBehind从头算 39 lowerBehind = 0; 40 } 41 j++; 42 } 43 // 有2个可能性: 44 // (1) break出来的, 那么maxPoten直接加入result, continue 45 // (2) j遍历完了整个数组, 说明maxPoten不可用, 那么计算lowerPoten 46 if (j == height.length) { 47 //说明是正常遍历完的, lower起作用了 48 //计算lowerPoten 49 //先算起初台阶的存水,这部分要区分对待 50 if (lower == -1) { 51 //说明也没找到lower, 说明就是一直降的台阶, 循环直接结束 52 break; 53 } 54 int stepWater = 0; 55 int k = 0; 56 if (union.size() > 0) {//计算台阶 57 while (k < union.size() && height[union.get(k)] > height[lower]) { 58 stepWater += height[i] - height[i + k + 1];//细节3, 计算step上的水量 59 k++; 60 } 61 } 62 //此外, maxPoten应截止到lower, lower后的水不能再算进去. 63 lowerPoten = maxPoten - stepWater - lowerBehind - (height[i] - height[lower]) * (lower - (i + k)); 64 result += lowerPoten; 65 i = lower; // i更新到lower位置 66 } else { 67 //说明是break出来的 68 result += maxPoten; 69 i = j; //i移动到j的位置 70 } 71 } 72 73 return result; 74 }
代码有点长,但是效率绝对高,leetCode上跑一遍全部用例,只用了5ms。
时间复杂度上来看,由于每次算出lower 或者 找到比 i 墙还高的墙之后, i 直接移到了lower或更高的墙去。 所以理想情况下是O(n)的复杂度。平均摊还上来看,也比较接近O(n)。
