论文阅读 DyREP:Learning Representations Over Dynamic Graphs

6 DyREP:Learning Representations Over Dynamic Graphs

link:https://scholar.google.com/scholar_url?url=https://par.nsf.gov/servlets/purl/10099025&hl=zh-CN&sa=X&ei=kIF4YrmVJ-OM6rQPxfOKUA&scisig=AAGBfm3I4EpwNkRLc5xhuaLEs47V0XWOzA&oi=scholarr

Abstract

摘要对动态图的嵌入提出了两个问题

1 如何在图上优雅地建模动态过程？

2 如何利用这种模型有效地将不断变化的图信息编码为嵌入？

他们提出了了一个模型DyRep，该模型将表示学习作为一个潜在的中间过程，连接两个观察到的过程：网络的动态（实现为拓扑演化）和网络上的动态（实现为节点之间的活动）

（原文：dynamics of the network (realized as topological evolution) and dynamics on the network (realized as activities between nodes)）

具体地说，本文提出了一个双时间尺度的深时序点过程模型（a two-time scale deep temporal point process model），该模型捕获了观测过程的交错动态。该模型由一个时序注意力嵌入网络进一步参数化，该网络将时间演化的结构信息编码为节点表示，进而驱动被观测动态图的非线性演化。

说人话就是作者用了基于时序点过程的注意力来捕获两个方面的信息 一个模型观测图级别的时序变化(拓扑演化：节点的增加和新边出现) 一个模型观测节点和边级别的时序变化(节点之间的活动：消息传递)，两个合起来做嵌入

Conclusion

本文提出了一种新的动态图建模框架，通过将嵌入作为潜在的中介过程，连接拓扑演化和节点交互的动态过程，有效地学习节点表示。

结尾提到该模型不支持网络收缩，原因有二：1很难获得具有细粒度删除时间戳的数据。2时序点过程模型需要更复杂的技术来支持删除。

Figure and table

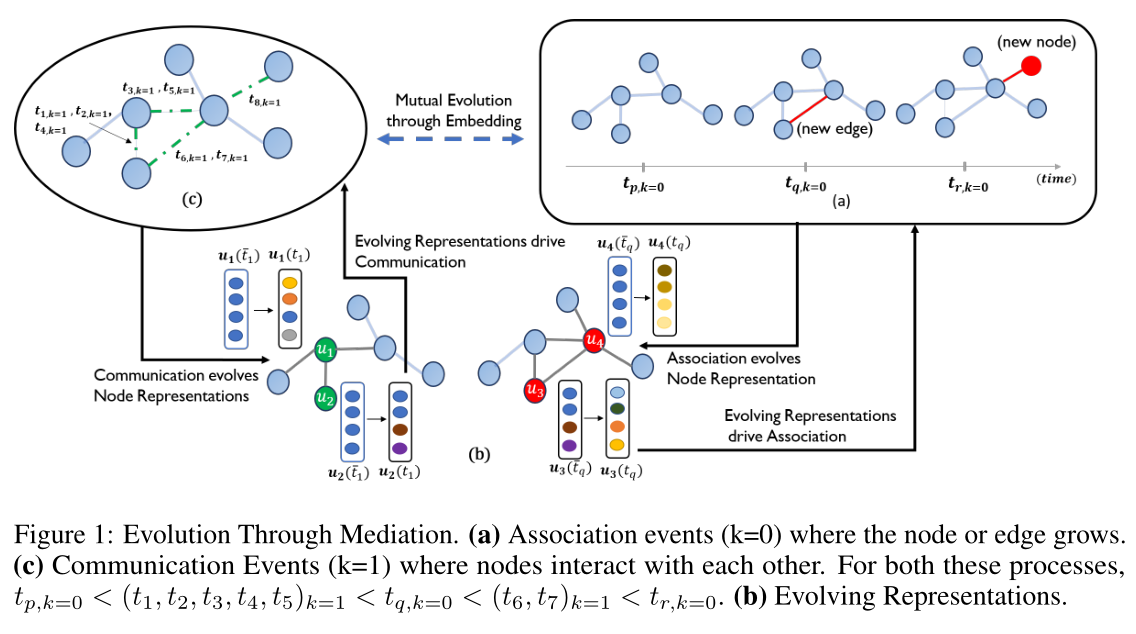
图1：算法嵌入的总览图。包含节点增加 边增加 交互的操作序列以及模型的嵌入流程

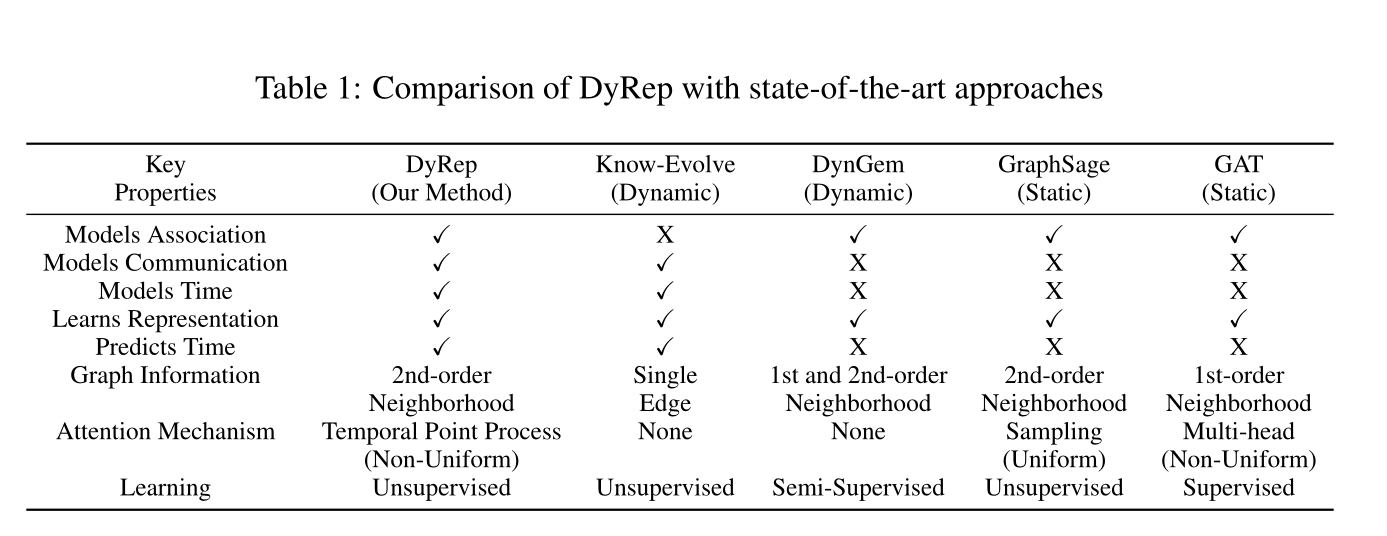
表1：各种算法的性质对照表（可以看到本文的注意力机制是基于时序点过程处理的）

图2：各模型在社交演化数据集和github数据集上的链路预测新效果。HITS@10效果放到了附录E中

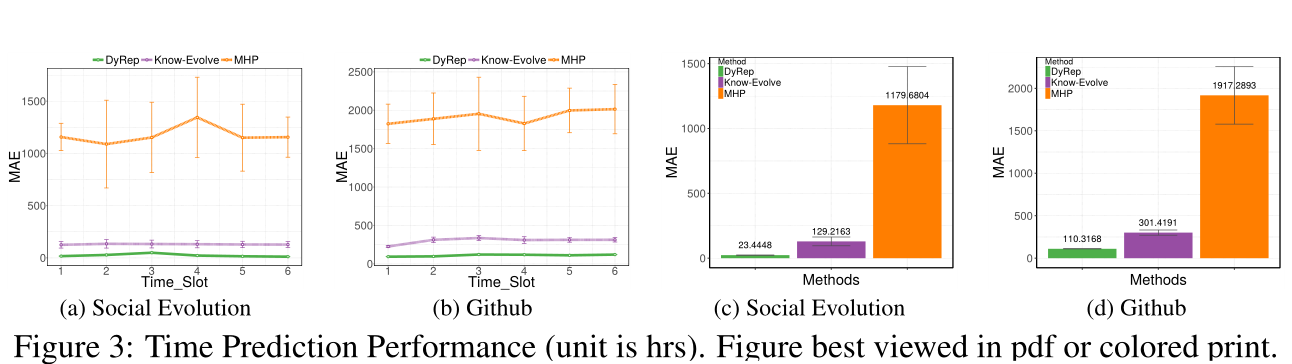
图3：事件时间预测表现

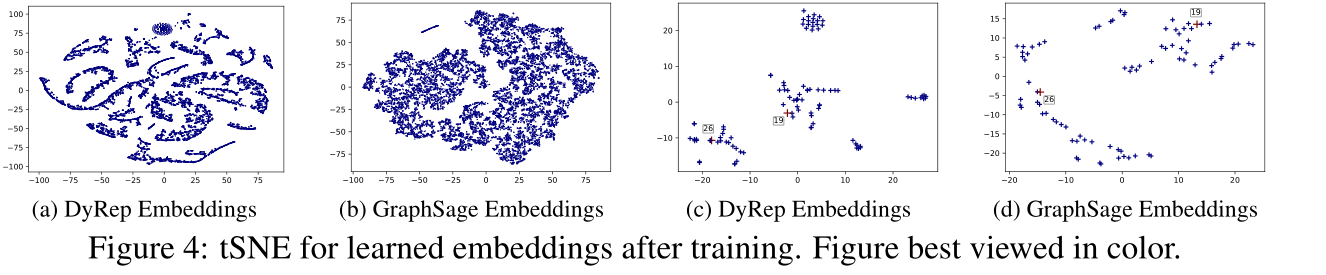
图4：训练后的embedding可视化

图5：局部嵌入传播

Introduction

摘要里的两个问题作者又提了一遍

1 如何在图上优雅地建模动态过程？

原来的工作将动态图的演变看做是单个时间维度的变化，而这篇论文提出大多数真实世界的图至少表现出两种不同的动态过程，它们在不同的时间尺度上演化

（1）拓扑演化：节点和边的数量预计会随着时间的推移而增长（或收缩），从而导致图中的结构变化；

（2）节点交互：与节点之间的活动有关，这些活动可能在结构上连接，也可能在结构上不连接。

对这些非线性演化的动态过程之间的交叉依赖，进行建模是推进动态图形式化模型的关键下一步。

2 如何利用这样的模型来学习能够有效捕获随时间变化的图形信息的动态节点表示？

现有的技术下可分类为两种方法

（1）DTDG：该方法将图上的演化过程看做若干个静态图的快照（比如DynGEM）。这些方法倾向于保留（编码）非常有限的结构信息，并在非常粗糙的级别捕获时间信息，这会导致快照之间的信息丢失，并且缺乏捕获细粒度时间动态的能力。这种方法的另一个问题是如何选择适当的聚合粒度。

（2）CTDG：连续时间方法，将图上的演化过程的粒度选择精细化。虽然现有方法已证明在特定环境下非常有效，但它们要么以解耦的方式建模简单的结构和复杂的时间特性，要么使用简单的时间模型（Continuous-Time Dynamic Network Embeddings）。但是，有几个地方表现出结构特性的高度非线性演化与复杂的时间动力学相耦合，有效地建模和学习捕捉此类复杂系统各种动力学特性的信息表示仍然是一个开放的问题。

如Natural algorithms and influence systems所述，有效学习此类动力系统的一个重要要求是能够在不同尺度上表达动力过程。所以本文提出，任何动态图都必须最小程度地表示为两个在不同时间尺度上演化的基本过程的结果：关联过程（网络的动态），它带来图结构的变化，并导致节点之间的信息传递；通信过程（网络上的动态），与节点之间（不一定连接）的活动有关，从而导致节点之间的临时信息传递。然后， 假设学习节点表示的目标是建模一个潜在的中介过程，该过程将上述两个观察到的过程连接起来，从而学习到的表示驱动这两个过程的复杂时间动态，这些过程随后导致节点表示的非线性演化。

此外，在图中传播的信息受节点与其邻域的链接和关联历史的时间动态控制。例如，在社交网络中，当一个节点的邻域增长时，它会改变该节点的表示，进而影响她的社交互动（链接→ 嵌入→ 消息传递）。类似地，当节点的交互行为发生变化时，它会影响其邻居和她自己的表示，而这反过来又会由于链接的添加或删除（消息传递→嵌入→链接）而改变其连接的结构和强度。 将这种现象称为“通过中介的进化”，并在图1中以图形方式加以说明。

本文提出了一个新的动态图表示学习框架DyRep，通过上面表达的潜在中介过程来模拟两个观察过程的交错演化，并随着时间的推移有效地学习更丰富的节点表示。随着时间的推移，框架以链接和消息传递的形式接收动态图信息，并在节点表示出现在这些事件中时更新它们。建立了一个双时间尺度的深时点过程方法来捕捉两个观测过程的连续时间细粒度时间动态。用一个深度归纳表示网络进一步参数化时间点过程的条件强度函数，该网络学习函数来计算节点表示。最后， 通过设计一种新的时间注意机制来耦合框架的结构和时间成分，该机制使用学习的强度函数在邻域节点上诱导时间注意。这使得 能够捕捉到随着时间推移控制节点表示的高度交错和非线性动态。 为框架的端到端培训设计了一个高效的无监督培训程序。

Method

2 BACKGROUND AND PRELIMINARIES

2.2 TEMPORAL POINT PROCESSES

https://zhuanlan.zhihu.com/p/65086715

这篇专栏里有具体解释（我也看的一知半解的 淦）

2.3 NOTATIONS AND DYNAMIC GRAPH SETTING

设\(\mathcal{G}_{t}=\left(\mathcal{V}_{t}, \mathcal{E}_{t}\right)\)是在\(t\)时刻\(\mathcal{G}\)的快照，\(\mathcal{V}_t\)是节点集，\(\mathcal{E}_t\)是边集。

事件观察：通信和关联过程都是以图\(\mathcal{G}\)上节点之间在时间窗口\([t_0，T]\)上观察到的以二元事件的形式实现的，并按时间排序。 对时间\(t\)的任何类型的事件使用以下规范元组表示，形式为\(e=(u，v，t，k)\)，其中\(u，v\)是事件中涉及的两个节点。\(t\)代表事件发生的时间。\(K∈ \{0，1\}\) 使用\(k=0\)表示拓扑演化过程（关联）中的事件，\(k=1\)表示节点交互过程（通信）中的事件。图中的边仅通过拓扑事件出现，而交互事件不会对其产生影响。所以\(k\)表示1：与生成拓扑（网络动态）的过程相关的范畴，2：互动事件（网络上的动态）这两点的抽象。然后， 将窗口\([0，T]\)中按时间排序的\(P\)个观测事件的完整集合表示为\(O=\{(u，v，t，k)_P\}^P_{p=1}\)。此处 $t_p ∈ \mathbb{R}^+, 0 ≤ t_p ≤ T $

节点表示：\(\mathbf{z}^{v} \in \mathbb{R}^{d}\)代表节点\(v\)的\(d\)维表示，随着时间的推移而演变，将其限定为时间的函数：\(\mathbf{z}^v(t)\)在时间\(t\)涉及\(v\)的事件之后更新的节点\(v\)表示。 使用\(\mathbf{z}^{v}(\bar{t})\)来表示t之前最近更新的节点v嵌入

动态图设置：\(\mathcal{G}_{t_0}=\left(\mathcal{V}_{t_0}, \mathcal{E}_{t_0}\right)\)作为图在t0时刻的初始快照。Gt0可能为空，也可能包含初始结构（关联边缘），但它不会有任何通信历史记录。框架将图形的演化视为一个事件流\(\mathcal{O}\)，因此任何新节点都将被视为此类事件的一部分。这将在数据可用的节点上引发自然排序。由于 的方法是归纳的，所以 从不学习特定于节点的表示，而是学习计算节点表示的函数。在这项工作中，只支持网络的增长，也就是说，本文只对节点和结构边的添加进行建模，并将删除作为未来的工作。此外，对于模型的一般描述， 将假设图中的边没有类型，节点没有属性。

3 PROPOSED METHOD: DYREP

该模型从两个层面（节点和边级别，图级别）观察图上的事件发生。比如在两个节点之间观察到事件时（消息传递即通信事件、边增加即交互事件），信息从一个节点流向另一个节点，并相应地影响节点的表示。虽然通信事件（或交互事件）仅在两个节点之间传播局部信息，但关联事件会改变拓扑结构，从而具有更大的全局影响。通过对观察到的局部事件进行编码，从而进一步了解这些事件的局部动态。

3.1 MODELING TWO-TIME SCALE OBSERVED GRAPH DYNAMICS

动态图上的观测包含两个交错复杂过程的时间点模式，分别以通信事件和关联事件的形式出现。在任何时间t，这些过程中的任何一个事件的发生取决于图的最新状态，即，两个节点将根据其最新表示参与任何事件。给定一个观测到的事件\(p=(u，v，t，k)\)， 使用条件强度函数\(λ_k^{u,v}(t)\)来定义时间点过程的连续时间深度模型，该函数对时间\(t\)时节点\(u\)和\(v\)之间事件\(p\)的发生进行建模：

\[\lambda_{k}^{u, v}(t)=f_{k}\left(g_{k}^{u, v}(\bar{t})\right) \]

其中

\(\bar{t}\)表示当前事件之前的时间点

$ g_k(\bar{t})\(计算两个节点\)\mathbf{z}^{u}(\bar{t}) \text { , } \mathbf{z}^{v}(\bar{t})$拼接后的嵌入表示

\[g_{k}^{u, v}(\bar{t})=\boldsymbol{\omega}_{k}^{T} \cdot\left[\mathbf{z}^{u}(\bar{t}) ; \mathbf{z}^{v}(\bar{t})\right] \]

其中\([;]\)表示拼接操作，\(\omega_{k} \in \mathbb{R}^{2 d}\)表示可学习的参数矩阵

如前所述，与沟通和关联过程相对应的动力学在不同的时间尺度上演化。为了说明这一点， 使用动态参数\(ψ_k\)参数化的softplus函数的修改版本来捕捉这种时间尺度依赖性

\[f_{k}(x)=\psi_{k} \log \left(1+\exp \left(x / \psi_{k}\right)\right) \]

其中\(x=g(\bar{t})\)，\(ψ_k(> 0)\)是可学习的时间尺度参数(该参数为标量)，作为训练的一部分。\(ψ_k\)对应于相应过程产生的事件速率。

3.2LEARNING LATENT MEDIATION PROCESS VIA TEMPORALLY ATTENTIVE REPRESENTATION NETWORK

前面在3.1节中介绍了如何计算节点表示，在事件发生后，需要更新两个参与节点的表示，以根据以下方法捕捉观察到的事件的影响：

局部嵌入传播：当事件中涉及两个节点构建路径或者消息传递时，该次事件对邻居的影响。在附录A中解释了这个组件的工作，具体见图5，在节点\(u\)和\(v\)之间观察到一个事件，\(k\)可以是0或1（即该事件可以是边构建或者消息传递）。\(\mathbf{h}_{\text {struct }}\)被计算来更新事件中涉及的每个节点。对于节点u，更新将来自\(\mathbf{h}_{\text {struct }}^{v}\)（绿色箭头），对于节点\(v\)，更新将来自\(\mathbf{h}_{\text {struct }}^{u}\)（红色箭头）。

请注意，所有嵌入都是动态演化的，因此每个事件后的信息流都是不同的，并以复杂的方式演化。通过这种机制，信息从节点u的邻居传递到节点v，从节点v的邻居传递到节点u。（1） 交互事件导致临时路径——此类事件可能发生在未连接的节点之间。在这种情况下，该流只会发生一次，但不会使\(u\)和\(v\)彼此相邻（例如，在会议上会面）。（2）拓扑事件导致永久路径——在这种情况下，\(u\)和\(v\)成为彼此的邻居，因此将有助于结构特性的发展（例如，成为学术朋友）。每侧蓝色箭头数量的差异分别表示每个节点对节点u和节点v的重要性不同。（我感觉要引入注意力了）

整体嵌入更新过程：作为起始点，邻居仅包括由初始边连接的节点。基于一次观察事件来说，通过下面的\(\mathbf{z}^{v}\left(t_{p}\right)\)式子来更新事件包含的两个节点的嵌入。对于节点\(u\)，等式第一项（Localized Embedding Propagation部分）\(\mathbf{h}_{\text {struct }}\)通过节点\(v\)从节点\(v\)的邻居\(N_v\)传递消息到节点\(u\)（可以将\(v\)视为从其邻居传递到\(u\)的消息传递者）。该信息用于更新节点u的嵌入。然而， 假设节点\(v\)不会将等量的信息从其邻居转发到节点u。相反，节点v会根据其与邻居的通信和关联历史（与每个邻居的重要性有关）接收其要转发的信息。这需要计算节点\(v\)与其相邻节点之间的结构边上的注意力系数。对于任何边缘， 都希望该系数取决于两个节点之间的事件速率（从而模拟现实世界中的现象，即一个人从与他互动更多的人那里获得更多信息）。因此， 用时间点过程参数\(\mathcal{S}_{u,v}\)来参数化 的注意力模块。算法1概述了计算该参数值的过程。算法1阐述了计算过程，将会在3.2.1中说明。

自传播：自传播可以看做是单个节点动态更新的最小组件。节点在嵌入空间中不是随机更新，而是对于先前位置进行更新（即节点的嵌入由上一次的嵌入基础上更新）。

外部驱动：在时间间隔内（例如，在涉及该节点的两个全局事件之间），一些外力可能会平滑地更新节点的当前特征。更新事件中涉及的每个节点。该信息用于更新节点\(u\)的嵌入。然而， 假设节点\(v\)不会将等量的信息从其邻居转发到节点\(u\)。相反，节点\(v\)会根据其与邻居的通信和关联历史（与每个邻居的重要性有关）接收其要转发的信息。这需要计算节点v与其相邻节点之间的结构边上的注意系数。对于任何边缘， 都希望该系数取决于两个节点之间的事件速率（从而模拟现实世界中的现象，即一个人从与他互动更多的人那里获得更多信息）。因此， 用时间点过程参数\(\mathcal{S}_{uv}\)来参数化 的注意力模块。算法1概述了计算该参数值的过程。
为了在 的设置中实现上述过程， 首先描述一个示例设置：考虑节点u和v在时间t参与任何类型的事件。\(\mathcal{N}_u,\mathcal{N}_v\)表示节点\(u,v\)的邻居，在这里讨论两个关键点

1）节点\(u\)充当将信息从\(\mathcal{N}_u\)传递到节点\(v\)的桥梁，因此\(v\)通过\(u\)以聚合形式接收信息。

2）当u的每个邻居将其信息传递给v时，节点u中继的信息由一个聚合函数控制，该聚合函数由u与其邻居的通信和关联历史参数化。

所以具体而言，对于节点\(v\)的第\(p\)个事件， 将\(z^v\)表示为

\[\mathbf{z}^{v}\left(t_{p}\right)=\sigma(\underbrace{\mathbf{W}^{\text {struct }} \mathbf{h}_{\text {struct }}^{u}\left(\overline{t_{p}}\right)}_{\text {Localized Embedding Propagation }}+\underbrace{\mathbf{W}^{r e c} \mathbf{z}^{v}\left(\bar{t}_{p}^{v}\right)}_{\text {Self-Propagation }}+\underbrace{\mathbf{W}^{t}\left(t_{p}-\bar{t}_{p}^{v}\right)}_{\text {Exogenous Drive }}) \]

其中：

\(\mathbf{h}_{\text {struct }}^{u} \in \mathbb{R}^{d}\)是从\(u\)的邻居经过聚合函数后得到的输出表示向量

\(\mathbf{z}^{v}\left(\overline{t_{p}^{v}}\right)\in \mathbb{R}^{d}\)是从先前的节点表示得到的当前状况

\(t_p\)是当前事件的时间点

\(\bar{t_p}\)表示当前事件之前的时间点（\(\bar{t_p}\)无限接近与\(t_p\)，但是不到\(t_p\)）

\(\bar{t_p^v}\)表示节点\(v\)上一个事件的时间点

\(\mathbf{z}^{v}\left(\bar{t}_{p}^{v}=0\right)\)可以使用来自数据集的输入节点特征或根据设置的随机向量来初始化节点\(v\)的初始表示

对于可训练矩阵\(\mathbf{W}^{\text {struct }}, \mathbf{W}^{r e c} \in \mathbb{R}^{d \times d} \text { and } \mathbf{W}^{t} \in \mathbb{R}^{d}\)

所以等式里的每一项都输出一个向量\(v \in \mathbb{R}^{d}\)然后求和作为节点嵌入更新

读到这里可以看见v节点的表示zv由上面三个部分（自传播，外部驱动，局部嵌入传播）构成，通俗的说这三个部分分别对应三个部分：从邻居的消息聚合+自己上一次的嵌入+时间间隔信息

*3.2.1 TEMPORALLY ATTENTIVE AGGREGATION

这节介绍了对邻居传递的消息做注意力的加权求和。

最近提出的注意机制在处理可变大小的输入方面取得了巨大的成功，将注意力集中在输入中最相关的部分，以便做出决策。然而，现有的方法认为注意力是一个静态量。在动态图中，改变节点之间的邻域结构和交互活动会随着时间的推移，使每个邻居对节点的重要性发生变化，从而使注意力本身成为一个时间上不断变化的量。此外，该数量取决于通过演化表示的相邻节点的关联和通信的时间历史。

最后，本文提出了一种新的基于时间点过程的注意机制，该机制利用时间信息计算节点间结构边缘的注意系数。然后使用这些系数计算嵌入传播所需的聚合量（\(\mathbf{h}_{\text {struct }}\)）。

其中

\(A（t） \in \mathbb{R}^{n \times n}\)是图\(G_t\)在\(t\)时刻的邻接矩阵，

\(\mathcal{S}(t) \in \mathbb{R}^{n \times n}\)是一个随机矩阵，捕捉时间t时两个顶点之间的强度

\(\mathcal{N}_{u}(t)=\left\{i: \mathbf{A}_{i u}(t)=1\right\}\)节点\(u\)在时间\(t\)的一跳邻居

为了形式化地捕捉不同邻域影响的差异，此处提出了一种新的基于条件强度的注意层，它使用矩阵S来诱导共享注意机制来计算邻域上的注意系数。

具体地说， 对给定的节点\(u\)执行局部注意，并计算与节点\(u\)的1跳邻居\(i\)相关的系数\(q_{u i}(t)=\frac{\exp \left(\mathcal{S}_{u i}(\bar{t})\right)}{\sum_{i^{\prime} \in \mathcal{N}_{u}(t)} \exp \left(\mathcal{S}_{u i^{\prime}}(t)\right)}\)，接着注意力权重就会用来计算节点u的信息聚合，式子如下

\[\mathbf{h}_{\text {struct }}^{u}(\bar{t})=\max \left(\left\{\sigma\left(q_{u i}(t) \cdot \mathbf{h}^{i}(\bar{t})\right), \forall i \in \mathcal{N}_{u}(\bar{t})\right\}\right)\\ \mathbf{h}^{i}(\bar{t})=\mathbf{W}^{h} \mathbf{z}^{i}(\bar{t})+\mathbf{b}^{h} \text { and } \mathbf{W}^{h} \in \mathbb{R}^{d \times d} \text { , } \mathbf{b}^{h} \in \mathbb{R}^{d} \]

\(\mathbf{z}^{i}(\bar{t}) \in \mathbb{R}^{d}\)是节点i的最新嵌入。max运算符的使用受一般点集学习的启发（Qi等人，2017年）。通过在元素方面应用最大池化算子，该模型有效地捕捉了邻域的不同方面。作者发现max的表现稍好一些，因为它考虑到了邻里关系的时间方面，如果使用平均值，邻里关系将被摊销（也就是有可能会抹除掉节点的结构信息，虽然在这里我感觉max也会）。

和图注意力网络的联系 本文提出的时间注意层与最近提出的图形注意网络（GAT）和门控注意网络（GaAN）（Zhang et al.，2018）的动机相同，重点是是在邻居之间应用非均匀注意。GAT和GaAN在静态图形设置方面都取得了显著的成功。GAT通过采用邻域上的多头非均匀注意来提高GraphSage，而GaAN通过在多头注意公式中对不同的头应用不同的权重来提高GAT。

重点：该文模型的关键创新之处在于，通过基于时间量\(\mathcal{S}\)的点过程对注意机制进行参数化，该时间量\(\mathcal{S}\)在不断演化，并驱动每个邻居对给定节点的影响。此外，与静态方法不同， 使用这些注意系数作为聚合器函数的输入，用于计算邻域的时间结构效应。最后，静态方法通过捕获多个表示空间来使用多头注意来稳定学习，但这是 这一层的固有属性，因为表示和事件强度随着时间的推移而更新，因此新事件有助于捕获多个表示空间。(点过程的注意力由于以往的事件和表示而改变，所以可以捕获多个表示空间？)

\(\mathcal{S}\)的构建和更新(上面代码的解释)： 构造一个随机矩阵\(S\)（在前面的部分中用于参数化注意）来捕获复杂的时间信息。在\(t=t_0\)， 利用\(\mathbf{A}(t_0)\)构建\(\mathcal{S}(t_0)\)。具体来说，对于给定的节点v，初始化相应行向量的元素\(\mathcal{S}_v(t_0)\)

for(node u : N[v])
{
    if(u == v || A[u][u] == 0)
    {
        s[v][u] = 0;
    }
    else
    {
        s[v][u] = 1/(N[v].size())
    }
}

在时间\(t>t_0\)观察到事件\(\mathcal{O}=(u，v，t，k)\)后，根据\(k\)的观察对\(\mathbf{A}\)和\(\mathcal{S}\)进行更新。具体来说，只会针对关\(\mathbf{A}\)联事件（\(k=0\)，结构变化）进行更新。请注意，是结构时间注意\(\mathcal{S}\)的参数，这意味着时间注意仅应用于节点的结构邻居。因此，\(\mathcal{S}\)值仅在两种情况下更新：

a）当前事件是已经具有结构边缘（\(\mathbf{A}_{uv}(t)=1\)和\(k=1\)）的节点之间的交互；

b）当前事件是关联事件（\(k=0\)）。

给定节点\(u\)的一个邻域，b代表每个边缘的基础注意，这是基于邻域大小的注意理（也就是\(\mathcal{S}_{v u}\left(t_{0}\right)=\frac{1}{\left|\mathcal{N}_{v}\left(t_{0}\right)\right|}\)）。每当发生涉及u的事件时，这种注意力会以以下方式发生变化：对于案例（a），使用事件的强度更新相应S条目的注意值。对于案例（b），重复与（a）相同的步骤，但也会随着邻域大小的增加，调整与其他邻域的边缘的背景注意（由\(b-b'\)更新、\(b\)和\(b’\)为新旧基础注意系数）。

4 EFFICIENT LEARNING PROCEDURE

当前模型的完整参数为\(\boldsymbol{\Omega}=\left\{\mathbf{W}^{\text {struct }}, \mathbf{W}^{r e c}, \mathbf{W}^{t}, \mathbf{W}^{h}, \mathbf{b}^{h}\right. , \left.\left\{\boldsymbol{\omega}_{k}\right\}_{k=0,1},\left\{\psi_{k}\right\}_{k=0,1}\right\}\)，对于观察到的时间集合\(\mathcal{O}\)， 通过最小化负对数似然来学习这些参数（loss function）

\[\mathcal{L}=-\sum_{p=1}^{P} \log \left(\lambda_{p}(t)\right)+\int_{0}^{T} \Lambda(\tau) d \tau \\ \]

其中

\(\lambda_{p}(t)=\lambda_{k_{p}}^{u_{p}, v_{p}}(t)\)表示时间t的事件强度

\(\Lambda(\tau)=\sum_{u=1}^{n} \sum_{v=1}^{n} \sum_{k \in\{0,1\}} \lambda_{k}^{u, v}(\tau)\)表示未发生事件的总生存概率

在附录H中的算法2采用了蒙特卡罗技巧的简单变体来计算对数似然方程的生存项。以减少时间复杂度。

具体如下：

算法2是计算对数似然方程生存项的蒙特卡罗技巧的简单变体。具体来说，在每个小批量中， 对非事件进行采样，而不是考虑所有非事件对（可能是数百万）。设\(m\)为最小批量，\(N\)为样本数。然后，算法2的复杂度将为\(O(2mkN)\)，其中系数2说明了每个事件中两个节点发生的更新，这表明了事件数量的线性可伸缩性。

整体训练程序采用了（Know-evolve: Deep temporal reasoning for dynamic knowledge graphs）的方法，其中时间反向传播（BPTT）训练是在全局序列上进行的，从而在避免梯度相关问题的同时，保持序列间事件之间的依赖性。实施细节见附录G。

Experiment

5 EXPERIMENTS

5.1 DATASETS

Social Evolution Dataset
节点: 83,

初始链接: 376,

最终链接:791,

交流次数: 2016339 ,

聚类系数: 0.548

Github Dataset

节点: 12328,

初始链接: 70640,

最终链接: 166565,

交流次数: 604649

聚类系数: 0.087.

5.2 TASKS AND METRICS

通过链接预测和事件时间预测

动态链接预测 当图形中的任意两个节点的交互事件发生率增加时，它们更有可能参与进一步的交互，最终这些交互可能会导致它们之间形成结构性联系。类似地，结构连接的形成可能会增加新连接节点之间相互作用的可能性。为了理解本文的模型捕捉到这些现象的能力，提出了这样的问题：在给定节点\(v\)，时间\(t\)，事件类型\(k\)的情况下，哪个节点\(u\)最有可能和\(v\)有链接？

可以计算时间t时此类时间的条件密度\(f_{k}^{u, v}(t)=\lambda_{k}^{u, v}(t) \cdot \exp \left(\int_{\bar{t}}^{t} \lambda(s) d s\right)\)

对于给定的测试记录\((u、v、t、k)\)， 用图中的其他实体替换v，并如上所述计算密度。然后， 按照密度的降序排列所有实体，然后计算Mean Average Rank (MAR) 和HITS(@10)

事件时间预测 这是一个相对新颖的应用，其目的是计算下一个特定类型事件（拓扑演化或者节点交互）可能发生的时间点。给定一对节点\((u，v)\)和时间t处的事件类型k， 使用上述密度公式计算时间t处的条件密度。然后，事件的下一个时间点可以计算为\(\hat{t}=\int_{t}^{\infty} t f_{k}^{u, v}(t)dt\)，其中积分没有解析形式，因此使用蒙特卡罗技巧估计它。对于给定的测试记录\((u、v、t、k)\)， 计算下一次通信事件可能发生的时间，并根据真实情况报告平均绝对误差（MAE）。

5.3 BASELINES

动态链路预测：Know-Evolve，DynGem ，DynTrd，GraphSage，Node2Vec

事件时间预测：Know Evolve，Multi-dimensional Hawkes Process

5.4 EVALUATION SCHEME

我们根据时间将测试集划分为n（=6）个时隙，并报告每个时隙的性能，从而提供不同方法的综合时间评估。

这节说明了对于不明确建模时间的动态基线（DynGem、DynTrd、GraphSage）和静态基线（Node2Vec），采用了一种滑动窗口训练方法和热启动方法，在初始训练集上学习，并测试第一个时隙。然后，我们从训练集的第一个时隙中添加数据，从训练集的起始位置删除等量的数据，并使用前一训练的嵌入重新训练模型。

5.5 EXPERIMENTAL RESULTS

通信事件预测性能 我们首先考虑预测节点之间可能有或可能没有永久边缘（关联）的通信事件的任务。图2（a-b）显示了相应的结果。

社交演化数据集

sota

Github数据集 所有方法在排名尺度上的总体性能都很低。如前所述，Github数据集非常稀疏，聚类系数非常低，这使得它成为一个具有挑战性的数据集。可以预期的是，对于大量没有通信历史的节点，大多数方法都会显示出类似的性能，但当有一些历史可用时，本文的方法优于所有其他方法。

关联事件预测性能

sota

时间预测性能

sota

定性表现：和graphsage比较嵌入，通过可视化可以看见DyRep嵌入具有更大的辨别力，因为它可以有效地捕捉到与实验证据一致的、随时间推移而变化的独特结构特征。

Summary

本文动态考虑了注意力函数，和DYSAT区别的是，本文用了时序点过程关注事件的发生来做注意力机制。而DYSAT使用的是自注意力的QKV矩阵，关注的是节点在时间步下的嵌入。目前读下来难度最大的一篇，也是最长的一篇 整体长度是其他论文的两倍。