1 Continuous-Time Dynamic Network Embeddings
Abstract
描述一种将时间信息纳入网络嵌入的通用框架,该框架提出了从CTDG中学习时间相关嵌入
Conclusion
描述了一个将时间信息纳入网络嵌入方法的通用框架。该框架为推广现有的基于随机游走的嵌入方法提供了基础,用于从连续时间动态网络学习动态(时间相关)网络嵌入
Figure and table
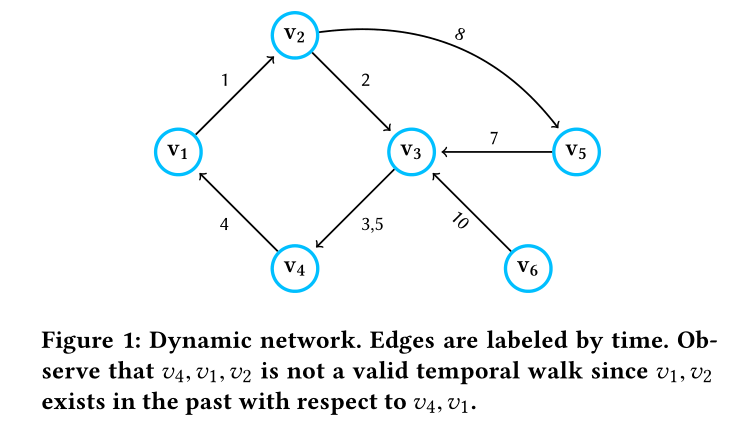
图1:这幅图的边标签为时间,注意v4 v1 v2不是一个合法的时序游走,因为v1v2的边时序小于v1v4的边
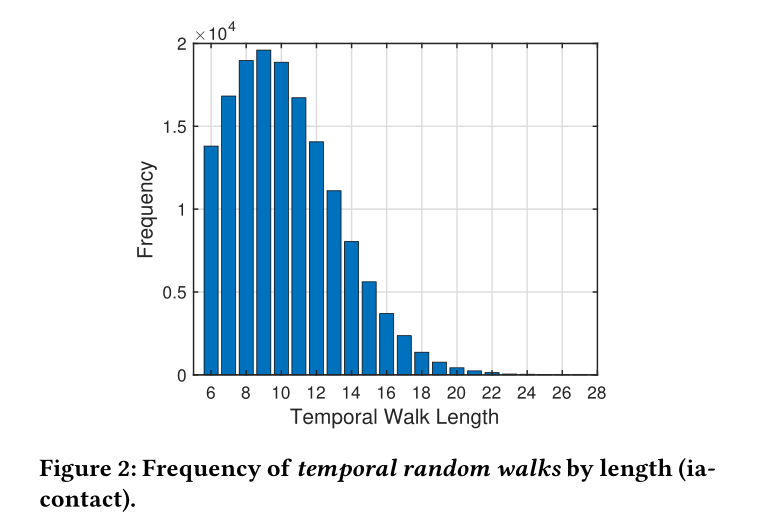
图2,可以看到大部分的时序随机游走长度都集中在右侧
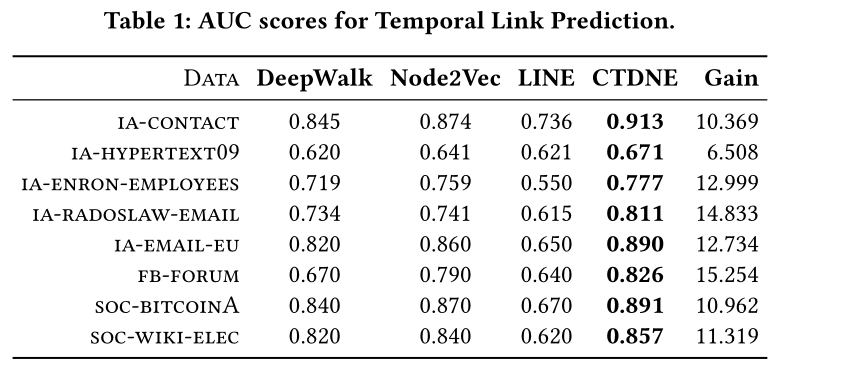
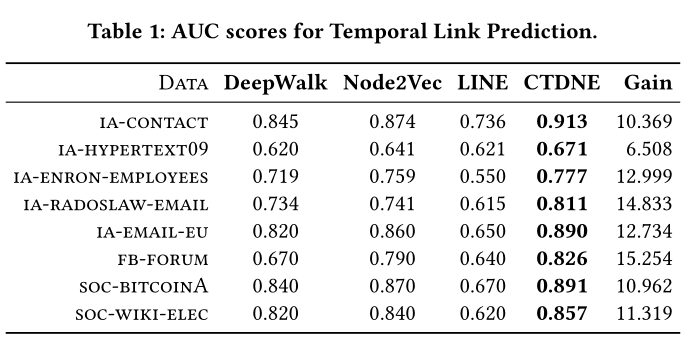
表1 SOTA
Introduction
在这个论文里 提出了一种通用框架。这个框架可以非常容易的和现有的节点嵌入方式(基于随机游走)结合,给这些节点嵌入加入时间序列信息。该框架是将时间依赖性纳入现有节点嵌入和基于随机游动的深度图模型的基础(就是基于时间序列的随机游走),并且由于保证时序是非递减的 可以减少虚假事件或者不可能的时间来减少噪声
静态图和动态图的区别就在于时间的粒度选择上 动态图尽量选择最小粒度的时间(如秒或者毫秒)来拟合连续的情况,但是如果对用snapshot的方法来看 时间粒度过小将会造成多个snapshot的计算和储存开销,该方法利用streaming graph的方式学习,可以用于要求实时性能的应用
所提出的方法在所有方法和图形中的平均增益为11.9%,结果表明,建模图中的时间依赖关系对于学习适当且有意义的网络表示非常重要。此外,任何使用随机游动的现有嵌入方法或深度图模型都可以受益于所提出的框架
作者说明了以往的随机游走的问题,例如是邮件发送接受构成的图,假设我们有两封电子邮件\(ei=(v1,v2)\)从\(v1\)到\(v2\),\(ej=(v2,v3)\)从\(v2\)到\(v3\);让\(T(v1,v2)\)为电子邮件\(ei=(v1,v2)\)发送的时间,让\(T(v2,v3)\)为电子邮件\(ej=(v2,v3)\)发送的时间。如果\(T(v1,v2)< T(v2,v3)\),那在第二封邮件中就可能反应了第一封邮件中的某些信息。反之,第二封邮件中就不会有第一封邮件中的信息。同样是v1到v2节点的随机游走,但是包含的信息不一样
这只是一个简单的例子,说明了建模实际事件序列(电子邮件通信)的重要性。忽略时间的嵌入方法容易出现许多问题,例如学习不适当的节点嵌入,这些节点嵌入不能准确捕捉网络中的动态,例如真实世界中的交互或节点之间的信息流
该方法具有以下三个特性
通用和统一框架:我们提出了一个通用框架,用于在节点嵌入和利用随机游动的深度图模型中合并时间依赖关系。
连续时间动态网络:学习连续时间动态网络的时间相关网络表示。该方法避免了从图的连续时间表示创建离散快照图序列时出现的问题和信息丢失。
有效:sota
Method
2.1 Temporal Model
这里对temporal model里的一些概念进行定义
2.2 Initial Temporal Edge Selection
这里说了自己和那些普通随机游走的区别:
普通随机游走是从某个点开始走固定长度的距离,但是在时序图中,由于时间边的存在,所以从分布中采样时不是随机选择一点v开始,而是
1.对初始时间进行采样,再去找离采样时间最近的边
2.或者直接对边和边对应的时间进行采样
这是所提出的使用时间随机游动的动态网络嵌入框架与在静态图上使用随机游动的现有方法之间的一个重要而根本的区别。
同时,也可以选择随机采样出一个边或者使用任意的加权分布进行采样,前面一种就是随机采样,而后面这个是我们可能希望从距离当前时间点更近的边缘开始更多的时间行走,因为遥远过去的事件/关系可能不太具有预测性或指示系统现在的状态
作者列了两个关于采样的三个公式
2.2.1:无偏
2.2.2:偏置
指数分布
该分布非常有利于时间较晚出现的边
线性分布
当两个边之间的相隔时间太长时,可以使用这个分布,先将\(e\)升序排序
\(\eta(e)\)返回\(e\)排序后的下标,对于最早时间的\(e\),\(\eta(e)=1\)
2.3 Temporal Random Walk
这段提到如何进行游走
首先定义邻居的概念:
对于\(t\)时刻下的点\(v\),该点邻居和在\(t^\prime\)时刻和\(v\)有时序边,且\(t^\prime>t\)
接着如何选择下一次的游走节点,注意到,从\(v\)到点\(u\)可能存在多个时序边,我们当然可以选择满足分布\(Γ_t (v)\)的边,但是考虑到可以更加直观的思考时间之间的连续性,例如,两个人可能会在一段时间内交换多封电子邮件,我们可能希望将抽样策略偏向于对连续边显示较小“中间”时间的行走。也就是说,对于随机行走中的每一对连续边\((u、v、t)\)和\((v、w、t+k)\),我们希望k较小。对于动态社交网络上的时间链接预测,限制“中间”时间时间让我们可以尝试不让不同时间段的朋友聚在一起的游走。例如,如果k很小,我们可能会对随机游动序列\((v1,v2,t)\),\((v2,v3,t+k)\)进行采样,这是有意义的,因为v1和v3更可能相互了解,因为v2最近与它们都进行了交互。另一方面,如果k很大,我们不太可能对序列进行采样。这有助于区分在非常不同的时间段与之互动的人,因为他们不太可能相互了解。
然后介绍三种分布进行采样

和一个Temporal context windows的概念

在对一组时序游走进行采样时,我们通常将\(\beta\)设置为\(N = |V |\) 倍
*2.4 Learning Time-preserving Embeddings
将上述问题转化为优化问题
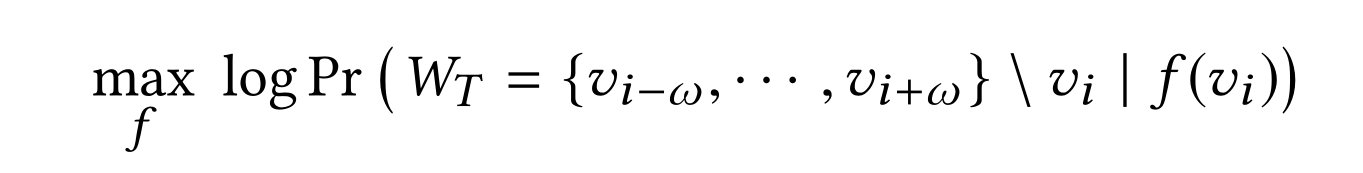
\(f\)是映射函数 将节点映射到\(embedding\)
\(W_T\)是一个任意时间的上下文窗口
这个式子的含义是,希望最大化\(log(Pr(A|B))\)这个函数,首先条件概率\(0<=Pr(A|B)<=1\),所以\(log(Pr(A|B))\)<=0,最大化\(log(Pr(A|B))\)即最大化条件概率\(Pr(A|B)\),该条件该率的含义为:在包含节点\(v_i\)时,将\(v_i\)通过\(f\)映射成\(embedding\),以这次映射的\(embedding\)为条件,时序随机游走产生的序列\(W_T\)出现的概率是多少,其中优化目标是\(f\),(优化时,\(W_T\)和\(v_i\)已经确定),所以希望函数\(f\)能够学习到一种将当前时序随机游走序列中的点\(v_i\)所对应的映射方法
如果假设时间上下文窗口的节点之间存在条件独立性 则
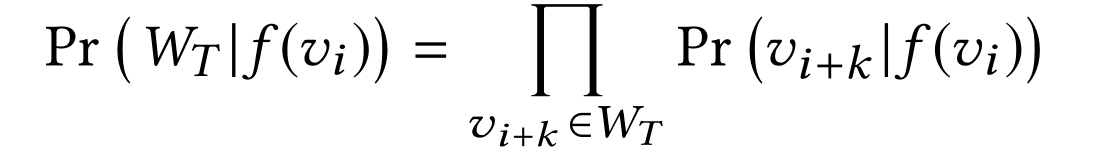
将上式的概率转换为可以计算的形式,则为每次下一次连接的点刚好为时间游走序列中顺序的点 例如有序列:
则每次为从图中选取到ABCDB作为序列的概率
后面作者补充,如果给定一个图G,设S是G上所有可能的随机游动的空间,设ST是G上所有时间随机游动的空间。很容易看出时间随机游动的空间ST包含在S中,而ST只代表S中可能的随机游动的一小部分。现有的方法是从S中随机采样一个序列进行节点的\(embedding\),而这项工作的重点就是从ST中进行采样序列。
一般来说,现有方法从S随机抽样到时间序列的概率非常小。当考虑时间时,绝大多数抽样中代表节点之间的事件序列都是无效的。例如,假设每个边缘代表两个人之间的交互/事件(例如,电子邮件、电话、空间接近),那么时间随机游走可能代表一条信息通过动态网络的可行路径或传染病传播的时间有效路径。
2.5 Hyperparameters
该模型只有一个需要调整的参数:指数基数(2.2和2.3中的指数分布)
该算法认为,可以接受任意长度的游走长度,只是将其限制在范围\([ω,L]\),\(ω\)和\(L\)之间任意大小的行走可以更精确地表示节点行为.
2.6 Model variants
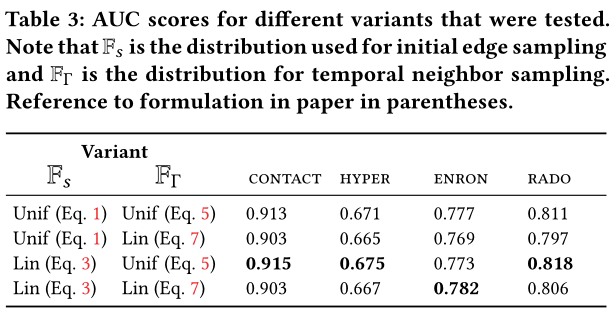
简单说,前面2.2有三种分布,2.3有三种分布,在3中做了这几种分布的排列组合产生模型的效果
Algorithm

Experiment
为了生成一组用于链接预测的标记示例,首先按时间(升序)对每个图中的边进行排序,并使用前75%进行表示学习。剩下的25%被视为正链接,随机抽取等量的负边。
baseline如下
3.1 Experimental setup
介绍一下相关参数


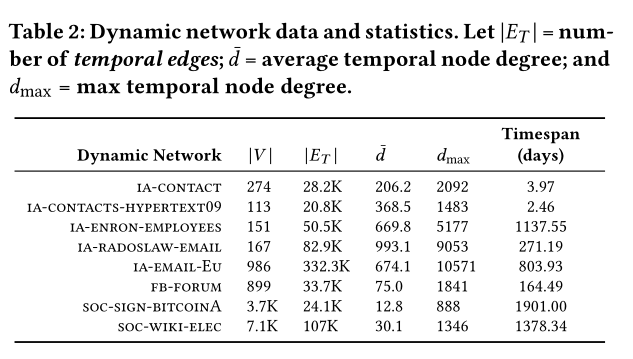
数据集的各项参数
排列组合两个分布(2.2,2.3中的分布)后 对不同数据集的效果
Summary
这篇文章是基于随机游走,核心思想就是提出了按照时序的随机游走,而不是任意游走,希望每次游走出来的路径都是一条时序边非递减的路径,并且提出了优化的目标函数算法,区别于node2vec的优化函数,该方法希望可以在节点\(vi\)条件下,令其时序游走序列出现的概率最大而不是令其近邻顶点出现的概率最大。