本系列文章将于2021年整理出版,书名《算法竞赛专题解析》。
前驱教材:《算法竞赛入门到进阶》 清华大学出版社
网购:京东 当当 想要一本作者签名书?点我
如有建议,请加QQ 群:567554289,或联系作者QQ:15512356
本文在公众号同步,阅读更方便:算法专辑
公众号还有暑假福利,免费连载作者的书:胡说三国
任何一个正整数(n)都可以唯一分解为有限个素数的乘积:(n = p_1^{c_1}p_2^{c_2}...p_m^{c_m}),其中(c_i)都是正整数,(p_i)都是素数且从小到大。
质因数分解有重要工程意义。在密码学中,需要对高达百位以上的十进制数分解质因子,因此发明了很多高效率的方法[1]。不过,大数的质因子分解是个难题,比寻找大素数要难得多,密码算法RSA就利用了大数难以分解的原理。
1、用试除法分解质因子
分解质因子也可以用前面提到的试除法。求(n)的质因子:
(1)第一步,求最小质因子(p_1)。逐个检查从2到(sqrt n)的所有素数,如果它能整除n,就是最小质因子。然后连续用(p_1)除(n),目的是去掉(n)中的(p_1),得到(n_1)。
(2)第二步,再找(n_1)的最小质因子。逐个检查从(p_1)到(sqrt {n_1})的所有素数。从(p_1)开始试除,是因为(n_1)没有比(p_1)小的素因子,而且(n_1)的因子也是(n)的因子。
(3)继续以上步骤,直到找到所有质因子。
最后,经过去除因子的操作后,如果剩下一个大于1的数,那么它也是一个素数,是(n)的最大质因子。这种情况可以用一个例子说明。大于(sqrt n)的素数也可能是(n)的质因子,例如6119 = 29*211,找到29后,因为29 ≥ (sqrt {211}),说明211是素数,也是质因子。
试除法的复杂度是(O(sqrt n)),效率很低。不过,在算法竞赛中,数据规模不大,所以一般就用试除法。
下面是试除法的代码[2]。因为试除法的效率不高,所以(n)用int型,没有用long long。
int p[20]; //p[]记录因子,p[1]是最小因子。一个int数的质因子最多有10几个
int c[40]; //c[i]记录第i个因子的个数。一个因子的个数最多有30几个
void factorization(int n){
int m = 0;
for(int i = 2; i*i <= n; i++)
if(n%i == 0){
p[++m] = i, c[m] = 0;
while(n%i == 0) //把n中重复的因子去掉
n/=i, c[m]++;
}
if(n>1) //没有被除尽,是素数
p[++m] = n, c[m] = 1;
}
2、用Pollard_rho启发式方法分解质因子
试除法的复杂度是(O(sqrt n)),也就是说,对到(B)的整数进行试除,可以完全获得到(B^2)的任意数的因子分解;用本节的pollard_rho算法,用同样的工作量,可以对到(B^4)的数进行因子分解[3]。需要指出的是,pollard_rho算法也仍然是一种低效的方法,比试除法好一点点,只能在算法竞赛的小规模数据中用用。
思考一个问题:如何快速找到一个大数的因子?不能像试除法那样从小到大一个个检查,太慢了。可以挑一些数来“试”,运气好说不定就碰到一个。这就是pollard_rho算法的思路,它使用了一个“随机”的方法来找。算法的主要内容只有2个:
(1)“随机”函数。实际上不是随机,而是一个启发函数:(x_i = (x_{i-1}^2 + c) mod n),其中(x)的初值(x_1)和(c)是随机数。计算的结果是生成了一个(x)序列,这个序列的前一部分(x_1,x_2,...,x_{j-1})不重复,后面的(x_j,x_{j+1},...,x_i)会重复并形成回路。rho指希腊字母"(
ho)",不重复的序列是(
ho)的“尾巴”,重复的回路是(
ho)的“身体”。
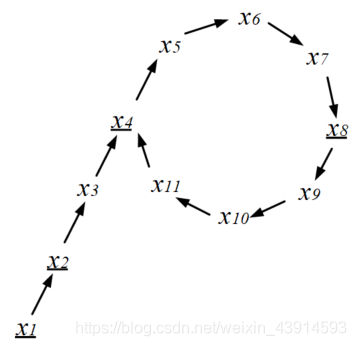
(2)计算(n)的一个因子。计算(d = gcd(y - x_i, n)),其中y是第(2^k)个(x),即第1、2、4、8、...个,见上图中划线的(x)。如果d ≠ 1且d ≠ n,d就是n的一个因子,原因很简单,gcd是求最大公约数,所以d肯定是n的因子。
从上面的描述可以看出,pollard_rho算法极为简单,读者可能怀疑它是否真的有效。确实,在一次(x)序列中,很可能计算不出因子,需要多次“随机”的(x)序列才能算出一个因子。令人惊讶的是,这个算法的效果还不错,它可以用(O(sqrt p))次计算找到(n)的一个小因子(p)。
pollard_rho的编码非常简单,见下面代码中的pollard_rho()函数。由于执行一次pollard_rho()只返回一个因子,要得到所有的因子,需要再写一个findfac()函数多次调用pollard_rho(),递归求得所有素因子。
//poj 1811题:输入一个整数n,2<=N<2^54,判断它是否为素数,如果不是,输出最小素因子。
typedef long long ll;
ll Gcd (ll a,ll b){ return b? Gcd(b, a%b):a;}
ll pollard_rho (ll n){ //返回一个因子,不一定是素因子
ll i=1, k=2;
ll c = rand()%(n-1)+1;
ll x = rand()%n;
ll y = x;
while (true){
i++;
x = (mult_mod(x,x,n)+c) % n; //mult_mod(x,x,n)功能是(x*x) mod n
ll d = Gcd(y>x?y-x:x-y, n); //重要:保证gcd的数大于等于0
if (d!=1 && d!=n) return d; //算出一个因子
if (y==x) return n; //已经出现过,直接返回
if (i==k) { y=x; k=k<<1;}
}
}
void findfac (ll n){ //找所有的素因子
if (miller_rabin(n)) { //用miller_rabin判断是否为素数
factor[tol++] = n; //存素因子
return;
}
ll p = n;
while (p>=n)
p = pollard_rho(p); //找到一个因子
findfac(p); //继续寻找更小的因子
findfac(n/p);
}