本系列文章将于2021年整理出版,书名《算法竞赛专题解析》。
前驱教材是:《算法竞赛入门到进阶》(京东 当当 ) 清华大学出版社。
如有建议,请联系:(1)QQ 群,567554289;(2)作者QQ,15512356
1、引子
提到状态压缩DP时,常常用Hamilton问题作为引子。
最短Hamilton路径 https://www.acwing.com/problem/content/description/93/
时间限制:3s。
题目描述:给定一个有权无向图,包括n个点,标记为0 ~ n-1,以及连接n个点的边,求从起点0到终点n-1的最短路径。要求必须经过所有点,而且只经过一次。1 ≤ n ≤ 20。
输入格式:第一行输入整数n。接下来n行每行n个整数,其中第i行第j个整数表示点i到j的距离(记为a[i, j])。0 ≤ a[i, j] ≤ 107
对于任意的x, y, z,数据保证 a[x, x]=0,a[x, y]=a[y, x] 并且 a[x, y]+a[y, z]>=a[x, z]。
输出格式:输出一个整数,表示最短Hamilton路径的长度。
暴力解法:枚举(n)个点的全排列,共(n!)个全排列。一个全排列就是一条路径,计算这个全排列的路径长度,需要做(n)次加法。在所有路径中找最短的路径,总复杂度是(O(n×n!))。
Hamilton问题是NP问题,没有多项式复杂度的解法。不过,用状态压缩DP求解,能把复杂度降低到(O(n^2×2^n))。当(n) = 20时,(O(n^2×2^n)) ≈ 4亿,比暴力法好很多。
首先定义DP。设(S)是图的一个子集,用dp[S][j]表示“集合S内的最短Hamilton路径”,即从起点0出发经过(S)中所有点,到达终点(j)时的最短路径;集合(S)中包括(j)点。根据DP的思路,让(S)从最小的子集逐步扩展到整个图,最后得到的(dp[N][n-1])就是答案,(N)表示包含图上所有点的集合。
如何求(dp[S][j])?可以从小问题(S-j)递推到大问题S。其中(S-j)表示从集合(S)中去掉(j),即不包含(j)点的集合。
如何从(S-j)递推到(S)?设(k)是(S-j)中一个点,把从0到(j)的路径分为两部分:((0→...→k) + (k→j))。以(k)为变量枚举(S-j)中所有的点,找出最短的路径,状态转移方程是:
(dp[S][j] = min{dp[S-j][k] + dist(j, k)})
其中(k)属于集合(S-j)。
集合(S)的初始情况只包含起点0,然后逐步将图中的点包含进来,直到最后包含所有的点。这个过程用状态转移方程实现。
上述原理见下面的图解。通过这个图,读者可以体会为什么用DP遍历路径比用暴力法遍历路径更有效率。
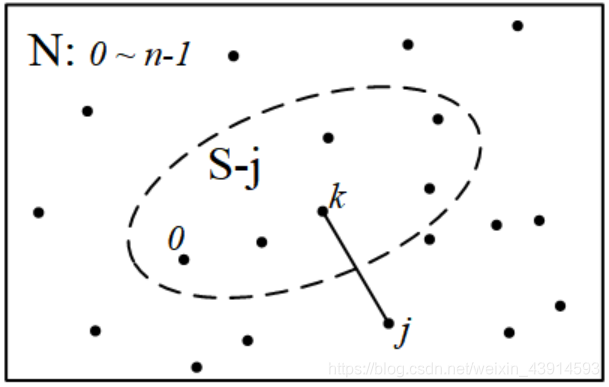
以上是DP的设计,现在关键问题是如何操作集合(S)?这就是状态压缩DP的技巧:用一个二进制数表示集合(S),即把(S)“压缩”到一个二进制数中。(S)的每一位表示图上的1个点,等于0表示(S)不包含这个点,等于1表示包含。例如(S) = 0000 0101,其中有两个1,表示集合中包含点2、0。本题最多有20个点,那么就定义一个20位的二进制数,表示集合(S)。
后面给出了代码,第一个(for)循环有(2^n)次,加上后面2个各(n)次的(for)循环,总复杂度(O(n^2×2^n))。
第一个(for)循环,实现了从最小的集合扩展到整个集合。最小的集合是(S) = 1,它的二进制数只有最后1位是1,即包含起点0;最大的集合是(S = (1<<n) - 1),它的二进制数中有(n)个1,包含了所有的点。
算法最关键的部分“枚举集合(S-j)中所有的点”,是通过代码中的两个if语句实现的:
if((S>>j) & 1),判断当前的集合S中是否有(j)点;
if((S^(1<<j)) >> k & 1),其中(S)^(1<<(j))的作用是从集合中去掉(j)点,得到集合(S-j),然后“>> k & 1”表示用(k)遍历集合中的1,这些1就是(S-j)中的点,这样就实现了“枚举集合(S-j)中所有的点”。注意,(S)^(1<<(j))也可以这样写:(S) - (1<<(j))。
这两个语句可以写在一起:if( ((S>>j) & 1) && ((S^(1<<j)) >> k & 1) ),不过分开写效率更高。
#include <bits/stdc++.h>
using namespace std;
int n, dp[1<<20][21];
int dist[21][21];
int main(){
memset(dp,0x3f,sizeof(dp)); //初始化最大值
cin>>n;
for(int i=0; i<n; i++) //输入图
for(int j=0; j<n; j++)
cin >> dist[i][j]; //输入点之间的距离
dp[1][0]=0; //开始:集合中只有点0,起点和终点都是0
for(int S=1; S<(1<<n); S++) //从小集合扩展到大集合,集合用S的二进制表示
for(int j=0; j<n; j++) //枚举点j
if((S>>j) & 1) //(1): 这个判断与下面的(2)一起起作用
for(int k=0; k<n; k++) //枚举到达j的点k,k属于集合S-j
if((S^(1<<j)) >> k & 1) //(2): k属于集合S-j。S-j用(1)保证
//把(1)和(2)写在一起,像下面这样,更容易理解,但是效率低一点:
//if( ((S>>j) & 1) && ((S^(1<<j)) >> k & 1) )
dp[S][j] = min(dp[S][j],dp[S^(1<<j)][k] + dist[k][j]);
cout << dp[(1<<n)-1][n-1]; //输出:路径包含了所有的点,终点是n-1
return 0;
}
类似的题目请练习:洛谷P1433 吃奶酪。
2、状态压缩DP的原理
从上面的“引子”可知,状态压缩DP的应用背景是以集合为状态,且集合一般用二进制来表示,用二进制的位运算来处理。
集合问题一般是指数复杂度的(NP问题),例如:(1)子集问题,设元素无先后关系,那么共有(2^n)个子集;(2)排列问题,对所有元素进行全排列,共有(n!)个全排列。
可以这样概况状态压缩DP的思想:集合的状态(子集或排列),如果用二进制表示状态,并用二进制的位运算来遍历和操作,又简单又快。当然,由于集合问题是NP问题,所以状态压缩DP的复杂度仍然是指数的,只能用于小规模问题的求解。
注意,一个问题用状态压缩DP求解,时间复杂度主要取决于DP算法,和是否使用状态压缩关系不大。状态压缩只是DP处理集合的工具,也可以用其他工具处理集合,只是不太方便,时间复杂度也差一点。
c语言的位运算有 "&","|","^","<<",">>"等,下面是例子。虽然数字是用十进制表示的,但位运算是按二进制处理的。
#include<bits/stdc++.h>
int main(){
int a = 213, b = 21; //a = 1101 0101 , b= 0001 1001
printf("a & b = %d
",a & b); // AND = 17, 二进制0001 0001
printf("a | b = %d
",a | b); // OR = 221, 二进制1101 1101
printf("a ^ b = %d
",a ^ b); // XOR = 204, 二进制1100 1100
printf("a << 2 = %d
",a << 2); // a*4 = 852, 二进制0011 0101 0100
printf("a >> 2 = %d
",a >> 2); // a/4 = 53, 二进制0011 0101
int i = 5; //(1)a的第i位是否为1
if((1 << (i-1)) & a) printf("a[%d]=%d
",i,1); //a的第i位是1
else printf("a[%d]=%d
",i,0); //a的第i位是0
a = 43, i = 5; //(2)把a的第i位改成1。a = 0010 1011
printf("a=%d
",a | (1<<(i-1))); //a=59, 二进制0011 1011
a = 242; //(3)把a最后的1去掉。 a = 1111 0010
printf("a=%d
", a & (a-1)); //去掉最后的1。 =240, 二进制1111 0000
return 0;
}
用位运算可以简便地对集合进行操作,下表给出了几个例子,并在上面的代码中给出了示例。
(1)判断a的第i位(从最低位开始数)是否等于1:
1 << ( i - 1 ) ) & a
(2)把a的第i位改成1:
a | ( 1<<(i-1) )
(3)把a的第i位改成0
a &(~(1<<i) )
(4)把a的最后一个1去掉:
a & (a-1)
在具体题目中需要灵活使用位运算。后面的例题给出了位运算操作集合的实际应用的例子,帮助读者更好地掌握。
3、poj 2411
这是状态压缩DP的经典题,其特点是“轮廓线”。
Mondriaan's Dream
题目描述:给定n行m列的矩形,用1×2的砖块填充,问有多少种填充方案。
输入格式:每一行是一个测试用例,包括两个整数:n和m。若n = m = 0表示终止。1 ≤ n, m ≤ 11。
输出格式:对每个测试用例,输出方案数。
摆放砖头的操作步骤,可以从第一行第一列开始,从左往右、从上往下依次摆放。横砖只占1行,不影响下一行的摆放;竖砖占2行,会影响下一行。同一行内,前列的摆放决定后列的摆放,例如第1列放横砖,那么第2列就是横砖的后半部分;如果第1列放竖砖,那么就不影响第2列。上下两行是相关的,如果上一行是横砖,不影响下一行;如果上一行是竖砖,那么下一行的同一列是竖砖的后半部分。
读者可以先对比暴力搜索的方法。用BFS搜索,从第一行第一列开始扩展到全局,每个格子的砖块有横放、竖放2种摆法,共m×n个格子,复杂度大约是(O(2^{m×n}))。
下面用DP解题。DP的思想是从小问题扩展到大问题,在这一题中,是否能从第一行开始,逐步扩展,直到最后一行?这一题的复杂性在于,一个砖块可能影响连续的2行,而不是1行,必须考虑连续2行的情况。
如下图所示,用一根虚线把矩形分为两半,上半部分已经填充完毕,下半部分未完成。把这条划分矩形的虚线称为“轮廓线”,这个概念将在下一节“插头DP”继续使用。
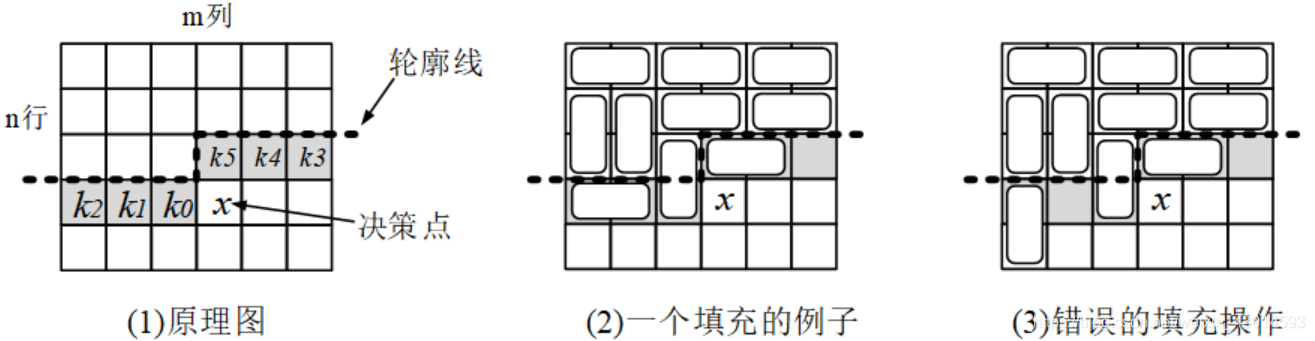
轮廓线下面的6个阴影方格(k_5k_4k_3k_2k_1k_0)表示当前的砖块状态,它跨越了2行。从它们推广到下一个方格(x),即递推到新状态(k_4k_3k_2k_1k_0x)。
(k_5k_4k_3k_2k_1k_0)有各种情况,用0表示没填砖块,用1表示填了砖块,有000000~111111共(2^6)种情况。图(2)是一个例子,其中(k_3)未填,(k_5k_4k_3k_2k_1k_0) = 110111。用二进制表示状态,这就是状态压缩的技术。
注意,根据DP递推的操作步骤,递推到阴影方格时,砖块只能填到阴影格本身和上面的部分,不能填到下面去。在图(3)中,把(k_2)的砖填到下面是错的。
这(2^6)种情况,有些是非法的,应该去掉。在扩展到(x)时,分析(2^6)种情况和(x)的对应关系,根据(x)是否填充砖块,有三种情况:
(1)(x) = 0((x)不放砖块)。如果(k_5) = 0((k_5)上没有砖块),由于(k_5)只剩下和(x)一起填充的机会,现在失去了这一机会,所以这个情况是非法的。如果(k_5) = 1,则(x) = 0可以成立。递推到(k_4k_3k_2k_1k_0x) = (k_4k_3k_2k_1k_00)。
(2)(x) = 1((x)放竖砖),只能和(k_5)一起放竖砖,要求(k_5)=0。递推到(k_4k_3k_2k_1k_0x) = (k_4k_3k_2k_1k_01)。
(3)(x)= 1((x)放横砖),只能和(k_0)一起放横转,要求(k_0) = 0,另外还应有(k_5) = 1。递推到(k_4k_3k_2k_1k_0x) = (k_4k_3k_2k_111)。
经过上述讨论,对(n)行×(m)列的矩阵,可以得到状态定义和状态转移方程。
状态定义。定义DP状态为dp([i][j][k]),它表示递推到第(i)行、第(j)列,且轮廓线处填充为(k)时的方案总数。
其中(k)是用(m)位二进制表示的连续(m)个方格,这(m)个方格的最后一个方格是就是第(i)行第(j)列的方格。(k)中的0表示方格不填充,1表示填充。m个方格前面的所有方格(轮廓线以上的部分)都已经填充为1。dp([n-1][m-1][(1<<m) -1])就是答案,它表示递推到最后一行、最后一列、(k)的二进制是(m)个1(表示最后一行全填充)。
时间复杂度是O((m×n×2^m))。
后面给出的代码用到了滚动数组,把二维([i][j])改为一维,状态定义改为dp([2][k])。
状态转移方程。根据前面分析的三种情况,分别转移到新的状态。
(1)(x) = 0,(k_5) = 1。从(k = k_5k_4k_3k_2k_1k_0 = 1k_4k_3k_2k_1k_0)转移到(k = k_4k_3k_2k_1k_00)。转移代码:
dp[now][(k<<1) & (~(1<<m))] += dp[old][k];
其中 ~(1<<m) 的意思是原来的(k_5) = 1移到了第m+1位,超出了(k)的范围,需要把它置0。
(2)(x) = 1,(k_5) = 0。从(k = k_5k_4k_3k_2k_1k_0 = 0k_4k_3k_2k_1k_0)转移到(k = k_4k_3k_2k_1k_01)。转移代码:
dp[now][(k<<1)^1] += dp[old][k];
(3)(x) = 1,(k_0) = 0,(k_5) = 1。从(k = k_5k_4k_3k_2k_1k_0 = k_5k_4k_3k_2k_11)转移到(k = k_4k_3k_2k_111)。转移代码:
dp[now][((k<<1) | 3) & (~(1<<m))] += dp[old][k];
其中 (k<<1) | 3 的意思是末尾置11;~(1<<m)是原来的(k_5) = 1移到了第m+1位,把它置0。
下面是poj 2411的代码[1]。
#include <iostream>
#include <cstring>
using namespace std;
long long dp[2][1<<11];
int now,old; //滚动数组,now指向新的一行,old指向旧的一行
int main(){
int n,m;
while( cin>>n>>m && n ){
if(m>n) swap(n,m); //复杂度O(nm*2^m), m较小有利
memset(dp,0,sizeof(dp));
now=0,old=1; //滚动数组
dp[now][(1<<m)-1]=1;
for(int i=0;i<n;i++) //n行
for(int j=0;j<m;j++){ //m列
swap(now,old); //滚动数组,now始终指向最新的一行
memset(dp[now],0,sizeof(dp[now]));
for(int k=0;k<(1<<m);k++){ //k:轮廓线上的m格
if(k & 1<<(m-1)) //情况(1)。要求k5=1
dp[now][(k<<1) & (~(1<<m))] += dp[old][k];
//原来的k5=1移到了第m+1位,置0
if(i && !(k & 1<<(m-1) ) ) //情况(2)
//i不等于0,即i不是第一行。另外要求k5=0
dp[now][(k<<1)^1] += dp[old][k];
if(j && (!(k&1)) && (k & 1<<(m-1)) ) //情况(3)
//j不等于0,即j不是第一列。另外要求k0=0, k5=1
dp[now][((k<<1) | 3) & (~(1<<m))] += dp[old][k];
//k末尾置为11,且原来的k5移到了第m+1位,置0
}
}
cout << dp[now][(1<<m)-1]<<endl;
}
return 0;
}
4、hdu 4539
排兵布阵
题目描述:团长带兵来到n×m的平原作战。每个士兵可以攻击到并且只能攻击到与之曼哈顿距离为2的位置以及士兵本身所在的位置。当然,一个士兵不能站在另外一个士兵所能攻击到的位置,同时因为地形的原因平原上也不是每一个位置都可以安排士兵。
现在,已知n, m(n <= 100, m <= 10 )以及平原阵地的具体地形,请你帮助团长计算该阵地最多能安排多少个士兵。
输入格式:包含多组测试数据。每组数据的第一行包括两个整数n和m,接下来的n行,每行m个数,表示n*m的矩形阵地,其中1表示该位置可以安排士兵,0表示该地形不允许安排士兵。
输出格式:对每组测试数据,输出最多能安排的士兵数量。
输入样例:
6 6
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 1 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
输出样例:
2
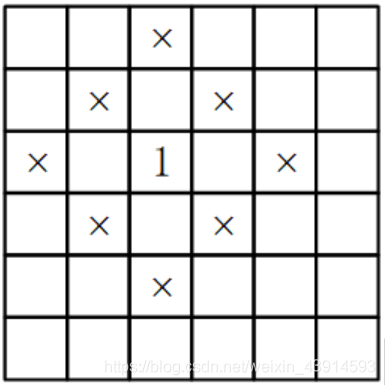
合法的安排见下图的例子,图中的'1'是一个站立的士兵,'×'是曼哈顿距离为2的攻击点,不能安排其他士兵。
这一题的思路比较容易。
首先考虑暴力法。对一个站立安排,如果图上的任意2个士兵都没有站在曼哈顿距离为2的位置上,就是一个合法的安排。但是一共有(2^{n×m})种站立安排,显然不能用暴力法一个个地判断。
下面考虑DP的思路。从第一行开始,一行一行地放士兵,在每一行都判断合法性,直到最后一行。假设递推到了第i行,只需要看它和第(i)-1行和第(i)-2行的情况即可:
(1)判断第i行自身的合法性。这一行站立的士兵,不能站在间隔2的位置上。例如m = 6时,合法的士兵站立情况有000010、000011、0000110、100011、110011等。
(2)判断第(i)行和第(i)-1行的合法性。第(i)行任何一个士兵,和第(i)-1行的士兵的间隔距离不能是2。
(3)判断第(i)行和第(i)-2行的合法性。
(4)判断第(i)-1行和第(i)-2行的合法性。
状态定义。定义d([i][j][k]):表示递推到第i行时的最多士兵安排数量,此时第(i)行的士兵站立情况是(j),第(i)-1行的士兵站立情况是(k)。在(j)、(k)的二进制表示中,0表示有士兵,1表示无士兵。
状态转移方程。从第(i)-1行递推到第(i)行:
dp[i][j][k] = max(dp[i-1][k][p]) + count_line(i, sta[j])
方程中的count_line(i, sta[j])计算第(i)行在合法的(j)状态下的士兵数量。用(p)遍历第(i)-2行的合法情况。
下面是代码[2]。代码中有4个for循环,复杂度是(O(nM^3))。M是预计算出的一行的合法情况数量,当m=10时,M = 169。用函数init_line()预计算一行的合法情况。
#include <bits/stdc++.h>
using namespace std;
int mp[105][12]; //地图
int dp[105][200][200];
int n,m;
int sta[200]; //预计算一行的合法情况。m = 10时,只有169种合法情况
int init_line(int n){ //预计算出一行的合法情况
int M = 0;
for(int i = 0; i < n; i ++)
if( (i&(i>>2)) == 0 && (i&(i<<2)) == 0 )//左右间隔2的位置没人,就是合法的
sta[M++] = i;
return M; //返回合法情况有多少种
}
int count_line(int i, int x){ //计算第i行的士兵数量
int sum = 0;
for(int j=m-1; j>=0; j--) { //x是预计算过的合法安排
if(x&1) sum += mp[i][j]; //把x与地形匹配
x >>= 1;
}
return sum;
}
int main(){
while(~scanf("%d%d",&n,&m)) {
int M = init_line(1<<m); //预计算一行的合法情况,有M种
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
scanf("%d",&mp[i][j]); //输入地图
int ans = 0;
memset(dp, 0, sizeof(dp));
for(int i = 0; i < n; i ++) //第i行
for(int j = 0; j < M; j ++) //枚举第i行的合法安排
for(int k = 0; k < M; k ++) { //枚举第i-1行的合法安排
if(i == 0) { //计算第1行
dp[i][j][k] = count_line(i, sta[j]);
ans = max(ans, dp[i][j][k]);
continue;
}
if((sta[j]&(sta[k]>>1)) || (sta[j]&(sta[k]<<1)))
//第i行和第i-1行冲突
continue;
int tmp = 0;
for(int p = 0; p < M; p ++){ //枚举第i-2行合法状态
if((sta[p]&(sta[k]>>1)) || (sta[p]&(sta[k]<<1))) continue;
//第i-1行和第i-2行冲突
if(sta[j]&sta[p]) continue; //第i行和第i-2行冲突
tmp = max(tmp, dp[i-1][k][p]); //从i-1递推到i
}
dp[i][j][k] = tmp + count_line(i, sta[j]); //加上第i行的士兵数量
ans = max(ans, dp[i][j][k]);
}
printf("%d
",ans);
}
return 0;
}
5、三进制状态压缩
除了用二进制做状态压缩,也可以用其他进制,例如三进制。
hdu 3001
题目描述:Acmer先生决定访问n座城市。他可以空降到任意城市,然后开始访问,要求访问到所有城市,任何一个城市访问的次数不少于1次,不多于2次。n座城市间有m条道路,每条道路都有路费。求Acmer先生完成旅行需要花费的最小费用。
输入:第一行是n,m,1 ≤ n≤ 10。后面有m行,有3个整数a、b、c,表示城市a和b之间的路费是c。
输出:最少花费,如果不能完成旅行,则输出-1。
本题n = 10,数据很小,但是由于每个城市可以走2遍,可能的路线就变成了((2n)!),所以不能用暴力法。
本题是旅行商问题的变形,编码方法和“1 引子”的Hamilton路径问题非常相似。阅读下面的题解时,请与“引子”的解释对照。
在普通路径问题中,一个城市只有两种情况:访问和不访问,用1和0表示,可以用二进制做状态压缩。但是这一题有三种情况:不访问、访问1次、访问2次,所以用三进制进行状态压缩,每个城市有0、1、2三种情况。
当n = 10时,路径有有(3^{10})种,对每种路径,用三进制表示。例如第14个路径,十进制14的三进制是(112_3),它的意思是:第3个城市走1次,第2个城市走1次,第1个城市走2次。
用tri[i][j]定义路径,它表示第(i)个路径上的城市(j)的状态。在上面的例子中,tri[14][3] = 1,tri[14][2] = 1,tri[14][1] = 2。函数make_trb()完成初始化计算,它把十进制14分解为三进制(112_3),并赋值给tri[i][j]。
状态定义。定义dp[j][i]:表示从城市(j)出发,按路径(i)访问(i)中所有的城市的最小费用。
状态转移方程。和“引子”中的图“枚举集合S - j中所有的点”类似,本题可以这样画图:
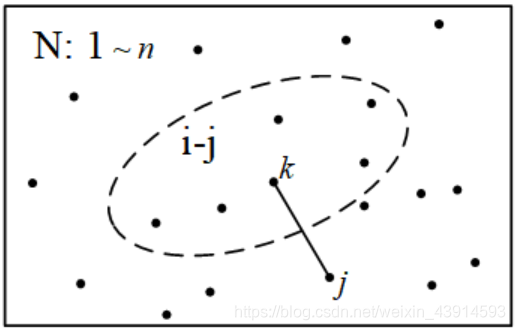
图中"(i-j)"的意思是从路径(i)中,去掉点(j)。从城市(j)开始访问路径(i),等于先走完路径"(i-j)",再走到城市(j)。用(k)遍历"(i-j)"中的所有城市,找到最少费用,得到状态转移方程:
dp[j][i] = min(dp[j][i], dp[k][(l)] + graph[k][j]);
其中(l = i - bit[j]),它涉及到本题的关键操作:如何从路径(i)中去掉城市(j)?
回顾“引子”的二进制状态压缩,是这样从集合(S)中去掉点(j)的:(S)^(1<<(j)),也可以这样写:(S) - (1<<(j))。
类似地,在三进制中,从(i)中去掉(j)的代码这样写:(i - bit[j]),其中(bit[j])是三进制第(j)位的权值。
下面是代码。有3个for循环,第一个(3^n)次,后两个分别n次,算法总复杂度是(O(3^nn^2)),当n = 10时,正好通过OJ测试。
#include<bits/stdc++.h>
const int INF = 0x3f3f3f3f;
using namespace std;
int n,m;
int bit[12]={0,1,3,9,27,81,243,729,2187,6561,19683,59049};
//三进制每一位的权值,与二进制的0, 1, 2, 4, 8...对照
int tri[60000][11];
int dp[11][60000];
int graph[11][11]; //存图
void make_trb(){ //初始化,求所有可能的路径
for(int i=0;i<59050;++i){ //共3^10=59050种路径状态
int t=i;
for(int j=1; j<=10; ++j){
tri[i][j]=t%3;
t/=3;
}
}
}
int comp_dp(){
int ans = INF;
memset(dp, INF, sizeof(dp));
for(int j=0;j<=n;j++)
dp[j][bit[j]]=0; //初始化:从第j个城市出发,只访问j,费用为0
for(int i=0;i<bit[n+1];i++){ //遍历所有路径,每个i是一个路径
int flag=1; //所有的城市都遍历过1次以上
for(int j=1;j<=n;j++){ //遍历城市,以j为起点
if(tri[i][j] == 0){ //是否有一个城市访问次数是0
flag=0; //还没有经过所有点
continue;
}
for(int k=1; k<=n; k++){ //遍历路径i-j的所有城市
int l=i-bit[j]; //l:从路径i中去掉第j个城市
dp[j][i]=min(dp[j][i],dp[k][l]+graph[k][j]);
}
}
if(flag) //找最小费用
for(int j=1; j<=n; j++)
ans = min(ans,dp[j][i]); //路径i上,最小的总费用
}
return ans;
}
int main(){
make_trb();
while(cin>>n>>m){
memset(graph,INF,sizeof(graph));
while(m--){
int a,b,c;
cin>>a>>b>>c;
if(c<graph[a][b]) graph[a][b]=graph[b][a]=c;
}
int ans = comp_dp();
if(ans==INF) cout<<"-1"<<endl;
else cout<<ans<<endl;
}
return 0;
}
代码改写自《算法竞赛入门经典训练指南》刘汝佳,陈锋,清华出版社,385页。原代码过于精妙难懂,本节做了较大改动。 ↩︎