堆排序

问题描述：

堆排序

问题解决：

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆节点的访问

通常堆是通过一维数组来实现的。在起始数组为 0 的情形中：

• 父节点i的左子节点在位置 (2*i+1);
• 父节点i的右子节点在位置 (2*i+2);
• 子节点i的父节点在位置 floor((i-1)/2);

堆的操作

在堆的数据结构中，堆中的最大值总是位于根节点。堆中定义以下几种操作：

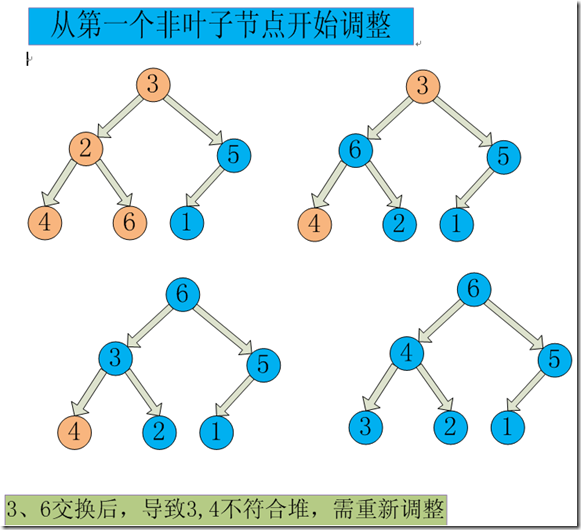
• 最大堆调整（Max_Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
• 创建最大堆（Build_Max_Heap）：将堆所有数据重新排序
• 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

堆排序算法时间复杂度：O(N * logN)

具体实现：

#ifndef HEADSORT_H
#define HEADSORT_H

#include<iostream>
#include <cmath>
#include <assert.h>
using namespace std;

#define BIGEST        ((unsigned)(~0)>>1)
#define SMALLEST    ~BIGEST

class HeapSort
{
private:
    int* arr;    
    int len;

    inline void swap(int& a,int&b)
    {
        int temp=a;
        a=b;
        b=temp;
    }

    inline int  parrent(int i)
    {
        return floor((double)i/2);
    }

    inline int lchild(int i)
    {
        return 2*i;
    }

    inline int rchild(int i)
    {
        return 2*i+1;
    }

    /**
    *    单个节点的最大堆调整
    */
    void MaxHeapify(int *array,int i)
    {
        int largest=i;
        assert(i<len);

        int l=lchild(i);
        if (l<=len && array[largest]< array[l])
        {
            largest=lchild(i);
        }

        int r=rchild(i);
        if (r<=len && array[largest]<array[r])
        {
            largest=rchild(i);
        }

        if (largest!=i)
        {
            swap(array[i],array[largest]);
            MaxHeapify(array,largest);
        }
    }

    /**
    *    所有元素最大堆调整
    */
    void MaxSort(int *smax)
    {
        memcpy(smax,arr,(len+1)*sizeof(int));
        for (int i=parrent(len);i>0;i--)
        {
            MaxHeapify(smax,i);
        }
    }

    /**
    *    单个节点小根堆调整
    */
    void MinHeapify(int *array,int i)
    {
        assert(i<=len);
        int minimum=i;

        int l=lchild(i);
        if (l<=len && array[l]<array[minimum])
        {
            minimum=l;
        }

        int r=rchild(i);
        if (r<=len && array[r]<array[minimum])
        {
            minimum=r;
        }

        if (minimum!=i)
        {
            swap(array[minimum],array[i]);
            MinHeapify(array,minimum);
        }
    }

    /**
    *    所有元素最小堆调整
    */
    void MinSort(int* smin)
    {
        memcpy(smin,arr,(len+1)*sizeof(int));
        for (int i=parrent(len);i>0;i--)
        {
            MinHeapify(smin,i);
        }
    }

public:
    HeapSort(int *array,int length=100)
    {
        len=length;
        this->arr=new int[len+1];
        this->arr[0]=0;    //数组第一个空出，元素从1开始编号
        memcpy(this->arr+1,array,len*sizeof(int));
    }

    /**
    *    输出原始数组
    */
    void getOringin()
    {
        for (int i=0;i<=len;i++)
        {
            cout<<arr[i]<<"	";
        }
    }

    /**
    *    输出大根堆
    */
    void getMaxHeap()
    {
        int *smax=new int[len+1];
        MaxSort(smax);
        for (int i=len;i>=1;i--)
        {
            cout<<smax[1]<<"	";
            smax[1]=SMALLEST;
            swap(smax[1],smax[i]);
            MaxHeapify(smax,1);
        }
　　　　 delete smax;　　//记住释放空间
        cout<<endl;
    }

    /**
    *    输出小根堆
    */
    void getMinHeap()
    {
        int *smin=new int[len+1];
        MinSort(smin);
        for (int i=len;i>0;i--)
        {
            cout<<smin[1]<<"	";
            smin[1]=BIGEST;
            swap(smin[i],smin[1]);
            MinHeapify(smin,1);
        }
 　　　　delete smin;　　//记住释放空间
        cout<<endl;
    }

　　//记住要析构　　
　　~HeapSort()
　　{
　　　　delete arr;
　　}

};
#endif

main函数：

#include "heap.h"

int main()
{
    int A[]={78,14,8,89,75,71,44,68,33};
    HeapSort heap(A,sizeof(A)/sizeof(int));

    cout<<"Origin:"<<endl;
    heap.getOringin();

    cout<<"Max Heapify:"<<endl;
    heap.getMaxHeap();

    cout<<"Min Heapify:"<<endl;
    heap.getMinHeap();
}