一 傅里叶级数
1 泰勒级数与欧拉公式
f(x)在定义域内存在连续N阶导数，则f(x)可以写成泰勒级数，如：
1） 
2）
3) 
观察以上级数，指数函数与三角函数可能存在一定关系，如ex=asin(x)+bcos(x)，设函数为eix（其中i为虚数），其傅里叶级数为：
，则可推出如下关系：eix=cosx + isinx （欧拉公式）。
2 在（-π,π）区间上的傅里叶级数
假设f(x)为在(-π,π)上的周期函数，且相信该函数可写成三角函数和
,
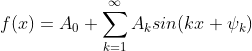使用三角函数和角公式可展开为：
，
在该和函数中，如果可以求出系数a与b, 则完成了傅里叶级数分解。由于未知参数个数远多于方程个数，无法使用代数方法得出a与b的值，这里需要利用积分来 完成系数求解。
由于三角函数的正交性（类比向量正交）可以简化运算结果，这里首先给出三角函数正交性结论：
1）
2）
3）
对左右同时在（-π,π）区间上积分，可得
；
对左右同时乘以cos(kx)再积分，可得
；
左右同时乘以sin(kx)再积分，可得
。
3 在任意周期上的傅里叶级数
观察发现，f(x)以2π为周期，其右边和式部分的周期序列为2π, π, 0.5π, 0.25π...；当f(x)以2a为周期时， 其右边和式部分周期序列应该为2a, a, 0.5a, 0.25a...， 则f(x)可分解为 
；对（-a, a）区间平移形成（-a + c, a + c）后仍然为一周期函数，且同样满足三角函数正交性相关性质， 故对以（-a + c, a + c）为周期的函数f(x), 有如下结论：
1）
2）
3）
4 ak与bk是否收敛？
f(x)是一个有界函数，其傅里叶系数ak, bk是无穷序列，当k趋近无穷大时，ak与bk是否趋近0？当k趋近无穷大时，三角函数周期趋近于无穷小， 在三角函数的一个周期内， f(x)函数值近似为一常数，则
；同理，bk亦如此。故ak与bk是否收敛。
5 傅里叶级数的指数形式
根据欧拉公式eix=cosx + isinx, e-ix=cosx - isinx, 可得 
，将其带人中整理得：
（在该式中，k 为正整数），观察发现可将指数项合并，同时k扩展为正负整数集（包括0），整理如下：
，系数ck与系数ak, bk关系如下：
1）当k=0时， c0 = a0；
2）当k>0时， ck = (ak - ibk) / 2；
3）当k<0时， ck = (a-k + ib-k) / 2；
当将周期函数写成时， 应该如何直接求取ck系数呢， 这里同样需要利用函数的正交性，具体如下：
1）
；
2）对左右同时乘以
并在（-a, a）区间上积分得：
。
二 傅里叶变换
周期函数f(x)的傅里叶级数指数形式为：
，
其中系数ck反应了函数f(x)在频率为k时（定义周期为2a时频率为1）的强度，当周期a趋近与无穷大时，可以将写成积分形式（积分的黎曼和表示），这就引入了连续变量下的傅里叶变换，推导如下：
=>
，其中方括号部分为ck；
=>
，由于a趋近无穷大，π/a趋近无穷小，令dλ=π/a, λ=kπ/a
=>
，外面的求和可以改写积分形式，如下：
=>
，其中方括号内积分为对原函数进行傅里叶变换，外面积分为相应的傅里叶逆变换。
根据以上推导，连续函数f(x)的傅里叶变换总结如下：
（傅里叶变换） 
（傅里叶逆变换）
以上推导中，使用dλ=π/a, λ=kπ/a进行变换，若改用dλ=1/2a, λ=k/2a，则有如下推导：
=>
,
=>
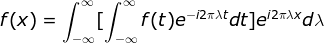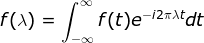(傅里叶变换）
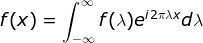（傅里叶逆变换）
三 离散傅里叶变换
1 关于冲激响应，卷积以及采样定理的一般结论
1）冲击串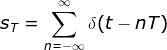
的傅里叶变换为
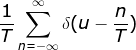，周期为T的冲激串的傅里叶变换是周期为1/T的冲激串；
2）信号分解表达式为：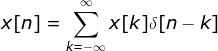
，
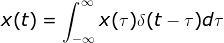，若单位冲击响应线性时不变，则响应函数定义的卷积函数，如下：
，
；
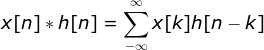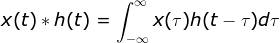3）对卷积进行傅里叶变换，等价于分别对信号与响应函数进行傅里叶变换后的乘积；对信号与响应函数的乘积的傅里叶变换，等价于分别对信号与响应函数进行傅里叶变换后的卷积：
，
。
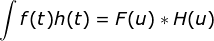4）
，
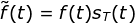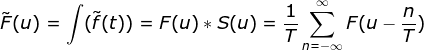，采样后函数的傅里叶变换是原函数傅里叶变换的一个无限拷贝，则只要取样周期T < 1 / (Umax * 2), 则取样函数可以完全恢复原函数；
2 离散傅里叶变换
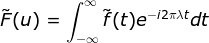（对采样函数进行傅里叶变换）
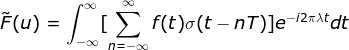（将采样函数与原函数关联）
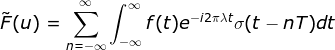，根据采样定理得：
。
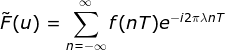假设在频率0到1/T间取M个等间距样本，则有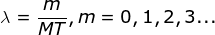
，
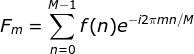（离散傅里叶变换），
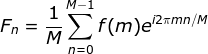（离散傅里叶反变换）。