在图像模式匹配中，可以使用图像矩不变量进行形态匹配，具体如下：
1 图像的矩
图像的(p + q)阶矩可表示为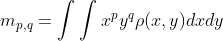 
，
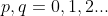当同一图像发生平移后，除了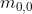 
保持不变，其他高阶矩均会发生改变，为了使图像矩的平移不变，需要引入中心矩。
使用以下公式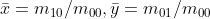 
可得到图像中心，
图像中心矩可表示为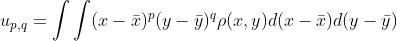 
。
图像中心矩与图像矩之间存在一个固定的关系，在时间计算中，一般可以遍历图像以求解到图像矩，
然后根据中心矩与矩之间的关系可直接计算出中心矩形，公式如下：
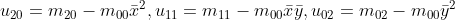
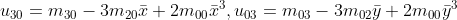
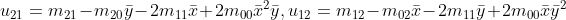
当同一图像发生缩放变化后，所有中心矩都发生了改变，为了保持缩放不变性，需要引入归一化中心矩。
定义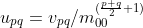 
可对中心矩归一化。
opencv 提供了函数 Moments moments(InputArray array, bool binaryImage=false ) 求解图像矩， 参数 array 可以是二值图像, vector<Point>， N*1 双通道Mat。
返回值 Moments 为一个结构体，定义如下
class Moments
{
public:
double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
double mu20, mu11, mu02, mu30, mu21, mu12, mu03;
double nu20, nu11, nu02, nu30, nu21, nu12, nu03;
}
2 旋转不变性
归一化中心矩可以达到平移，缩放不变性，但对于同一图像做任意旋转，归一化中心矩无法满足旋转不变性。
1) 代数不变量
对于二项式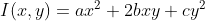 
，对变量 x，y 做旋转变换 
，
得到 
，满足 
。
因此， 二项式满足严格的旋转不变性，即代数不变量。
2）矩不变量
根据代数不变量性质，归一化图像中心矩为变量x,y的多项式表达，如果可以构造出类似二项式表达式，则该表达式满足旋转不变性。
MING-KUEI HU 在归一化中心矩基础构造出了7个hu矩以满足旋转不变量，具体如下：
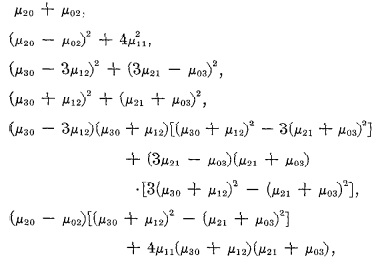
opencv 提供了函数 void HuMoments(const Moments& moments, double hu[7]) 函数来计算7个HU矩，
通过比较各个形状对应的HU矩，可以对相似形状进行匹配。
参考资料 Learning OpenCV 3 Adrian Kaehler & Gary Bradski
Visual Pattern Recognition by Moment Invariants MING-KUEI HU