1 频域滤波基础
对一幅数字图像,基本的频率滤波操作包括:
1)将图像变换到频率域;
2)根据需要修改频率域数值;
3)反变换到图像域。
使用公式表达为  ,
,
H(u,v) 为滤波器(滤波传递函数),F(u,v) 为图像函数的傅里叶变换。
在将图像变换到频率域之前,对其中心化处理可使变换后结果更利于观察与分析,因此,乘以 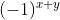 以实现中心化。
以实现中心化。
在反变换到图像域后,得到的图像是 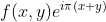 ,将其乘以
,将其乘以  使图像平移还原,因此,乘以
使图像平移还原,因此,乘以 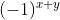 还原平移。
还原平移。
在对数字图像进行频移滤波时,需要关注卷积缠绕和振铃现象,这是在设计滤波函数时需要尽力避免的。
1)卷积缠绕
给定非周期信号,对其进行离散傅里叶变换或者反变换后得到周期信号,而周期信号卷积操作可能产生缠绕。
卷积操作是对两个信号滑动乘积进行累加,当累加区间大于任意信号周期,就可能对一个信号周期外的值进行重复累加。
解决卷积缠绕的方法就是在傅里叶变换(或反变换前)进行0填充处理,0填充使得信号周期不小于卷积区间,从而避免了卷积缠绕。
2)振铃
使用0填充可以避免卷积缠绕,但可能产生振铃现象。
公式  使用频域乘积进行滤波处理,其等价操作为空间域的卷积
使用频域乘积进行滤波处理,其等价操作为空间域的卷积 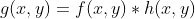 。
。
当 H(u,v) 为理想低通滤波器(盒函数),其反傅里叶变换 h(x,y) 包含无限震荡频率,无限震荡频率使得在卷积时必然产生振铃现象。
如果对其进行0填充以避免卷积缠绕,必然对 f(x,y)信号截断, 对截断后的 f(x,y) 变换到频率域,发现之前的盒函数在边缘上出现了震荡,使振铃现象更加严重。
综上描述,对于理想低通滤波器,振铃现象不可避免,如果0填充以避免卷积缠绕将使得振铃现象更加明显。
一个折中方案就是对图像进行0填充,但不对滤波器进行填充, 由于图像0填充在一定程度降低了卷积缠绕的影响,
同时由于图像0填充使得理想低通滤波器引起的振铃现象减弱,从而得到相对理想的结果。
一个更好的方案是使用高斯低通滤波器,由于高斯函数的傅里叶变换(或反傅里叶变换)均为高斯函数,高斯函数没有震荡周期,故天然没有振铃现象。
仅需要对图像0填充以避免卷积缠绕即可得到较好的滤波结果。
通过讨论,可以得到频域滤波的完整步骤如下:
1)将给定一幅 M*N 的图像 f(x,y) 0填充为 2M*2N 的图像 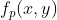 ;
;
2)对  乘以
乘以 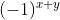 平移到中心,并对器进行傅里叶变换
平移到中心,并对器进行傅里叶变换 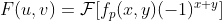 ;
;
3)使用滤波器滤波 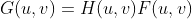 ;
;
4)对滤波后频率进行反傅里叶变换 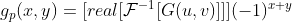 ,
,
其中,real 表示取反傅里叶变换的实部,这是因为数值计算过程中不可避免的误差而导致虚部寄生分量,
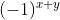 抵消到傅里叶变换前的平移到中心操作;
抵消到傅里叶变换前的平移到中心操作;
5)从 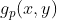 中取左上 M*N 图像即为滤波后结果。
中取左上 M*N 图像即为滤波后结果。
2 低通滤波器
1)理想低通滤波器(ILPF)
理想低通滤波器定义为 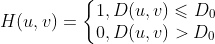 ,D(u,v) 为 (u,v) 到中心点距离,
,D(u,v) 为 (u,v) 到中心点距离,
由于理想低通滤波器为一盒函数,其空域卷积核存在震荡特性,这使得理想低通滤波天然存在振铃现象。
2)布特沃斯低通滤波器(BLPF)
布特沃斯低通滤波器定义为 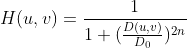 ,当 n 越大时,布特沃斯滤波器越接近理想滤波器,
,当 n 越大时,布特沃斯滤波器越接近理想滤波器,
因此,变换到空间域后其卷积核的震荡性随着 n 增大而增大。
当 n=1 时,变换到空间域其卷积核没有震荡,但其频率截止曲线过于平滑,图像平滑效果较差。
当 n=2 时,变换到空间域其卷积核有轻微震荡,但其产生的振铃现象不大,同时具有较好的平滑性,因此 n=2 可作为一个折中方案,
使用不同的截止频率 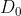 ,可以控制图像平滑程度,达到不同滤波效果。
,可以控制图像平滑程度,达到不同滤波效果。
3)高斯低通滤波器(GLPF)
高斯低通滤波器定义为 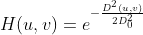 ,
,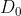 为滤波截止频率。
为滤波截止频率。
由于高斯函数的傅里叶变换(或反傅里叶变换)均是高斯函数,因此,其卷积核没有振铃现象。
综上,似乎高斯低通滤波器是最优的选择,一般情况下这个结论是正确的。
但是由于2阶布特沃斯低通滤波器具有更陡峭的频率截止曲线,同时其振铃现象较小,
在一些需要对频率严格分割的情况下,2阶布特沃斯低通滤波器应该是一个较好的选择。
理想低通滤波器会产生较严重的振铃现象,因此一般都不是一个较好的选择!
3 高通滤波器
有了低通滤波器,对其进行适当取反操作,即可以得到合适的高通滤波器。
1)理想高通滤波器(IHPF)
理想高通滤波器定义为 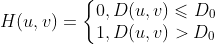 ,
,
同样的,由于其反傅里叶变换具有震荡性,因此同样会产生振铃现象,这一般不是一个好的的选择。
2)布特沃斯高通滤波器(BHPF)
布特沃斯高通滤波器定义为 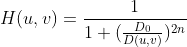 ,
,
2阶布特沃斯高通滤波器的反傅里叶变换具有可以接受的较小震荡性,这是一个高通滤波的选择。
3)高斯高通滤波器(GHPF)
高斯高通滤波器定义为 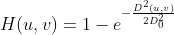 ,
,
高斯高通滤波器的反傅里叶变换没有震荡特性,因此滤波后不会产生振铃,这是一个好的高通滤波选择。
参考资料 Digital Image Processing Rafael C. Gonzalez & Richard E. Woods