一、暴力枚举
1、实现代码
def fib(n):
f = [1,1]
for i in range(2,n+1):
f.append(f[-1]+f[-2])
print(f)
return f(n)
fib(5)
2、输出
"C:Program FilesPython35python.exe" E:/工作目录/python/test/DP.py [1, 1, 2, 3, 5, 8] Process finished with exit code 1
二、动态规划定义
1、什么是动态规划?
动态规划的英文名,是一种分阶段求解决策略的数学思想,它不止用于编程领域,也用于管理学,经济学、生物学
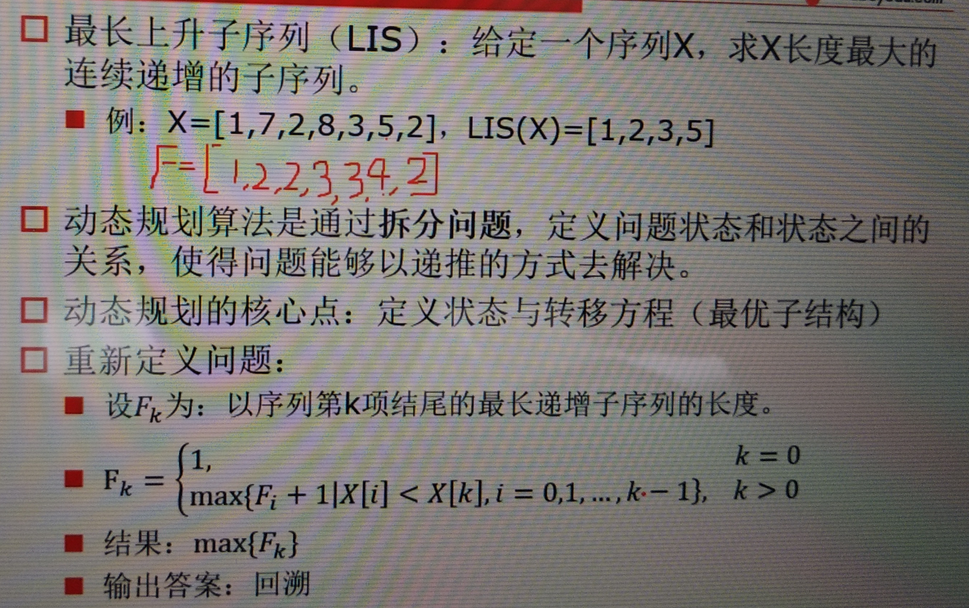
2、初始为1
实现代码
def LTS(x):
F = [0 for _ in range(len(x))]
F[0] = 1
for k in range(1,len(F)):
max_loc = None
max_num = 0
for i in range(1,k):
if x[i] < x[k]:
if F[i] > max_num:
max_loc = i
max_num = F[i]
F[k] = max_num + 1
return F
print(LTS([1,7,2,8,3,5,2]))
输出
"C:Program FilesPython35python.exe" E:/工作目录/python/test/DP.py [1, 1, 1, 2, 2, 3, 1] Process finished with exit code 0
2、初始为0
1、实现代码
def LIS(x):
F = [0 for _ in range(len(x))]
#初始化
F[0] = 1
for k in range(1,len(F)):
max_loc = None
max_num = 0
#内层循环表示[0:R] 里所有小于x[k]的对应位置的F[i]最大值
for i in range(0,k):
if x[i] < x[k]:
if F[i] > max_num:
max_loc = i
max_num = F[i]
F[k] = max_num + 1
return F
print(LIS([1,7,2,8,3,5,2]))
2、输出
"C:Program FilesPython35python.exe" E:/工作目录/python/test/DP.py [1, 2, 2, 3, 3, 4, 2] Process finished with exit code 0
三、动态规划最长上升子序列

1、实现代码
def fib(n):
f = [1,1]
for i in range(2,n+1):
f.append(f[-1]+f[-2])
print(f)
return f(n)
# fib(5)
def LIS(x):
F = [0 for _ in range(len(x))]
p = [-1 for _ in range(len(x))]
#初始化
F[0] = 1
p[0] = -1
for k in range(1,len(F)):
max_loc = -1
max_num = 0
#内层循环表示[0:R] 里所有小于x[k]的对应位置的F[i]最大值
for i in range(0,k):
if x[i] < x[k]:
if F[i] > max_num:
max_loc = i
max_num = F[i]
F[k] = max_num + 1
p[k] = max_loc
max_i = 0
for i in range(1,len(F)):
if F[i] > F[max_i]:
max_i = i
lis = []
i = max_i
while i >= 0:
lis.append(x[i])
i = p[i]
lis.reverse()
return lis
print(LIS([1,7,2,8,3,5,2]))
2、输出结果
"C:Program FilesPython35python.exe" E:/工作目录/python/test/DP.py [1, 2, 3, 5] Process finished with exit code 0
最长公共子序列2

最长公共子序列1

动态规划最优子结构
