一、基本原理
计数排序的思想类似于哈希表中的直接定址法,在给定的一组序列中,先找出该序列中的最大值和最小值,从而确定需要开辟多大的辅助空间,每一个数在对应的辅助空间中都有唯一的下标。
- 找出序列中最大值和最小值,开辟Max-Min+1的辅助空间
- 最小的数对应下标为0的位置,遇到一个数就给对应下标处的值+1,。
- 遍历一遍辅助空间,就可以得到有序的一组序列
限制:计数排序假设n个输入元素中的每一个元素都是在0到k区间内的一个整数,只可处理非负数;计数排序的基本思想:对每一个元素x,确定小于x的元素个数,利用这一信息,就可以直接把x放到输出排序数组的正确位置上了。

二、图解排序过程
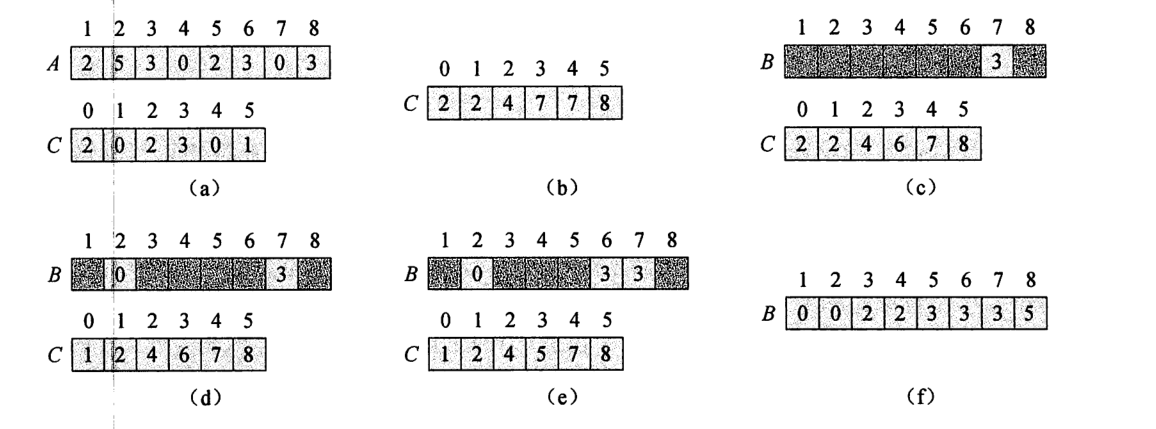
三、实现代码
import random
def count_sort(li,max_num = 100):
count = [0 for i in range(max_num+1)]
for num in li:
count[num] += 1
li.clear()
for i,val in enumerate(count):
for _ in range(val):
li.append(i)
li = [random.randint(0, 100) for i in range(100000)]
count_sort(li)
print(len(li))
打印结果
"C:Program FilesPython35python.exe" E:/count.py
100000
Process finished with exit code 0
四、性能分析
1、和系统自带的速度比较
import random
import time
import copy
import sys
from collections import deque
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
@cal_time
def count_sort(li,max_num = 100):
count = [0 for i in range(max_num+1)]
for num in li:
count[num] += 1
li.clear()
for i, val in enumerate(count):
for _ in range(val):
li.append(i)
@cal_time
def sys_sort(li):
li.sort()
li = [random.randint(0, 100) for i in range(100000)]
li1 = copy.deepcopy(li)
count_sort(li)
sys_sort(len(li))
输出结果
"C:Program FilesPython35python.exe" E:/python/test/count.py
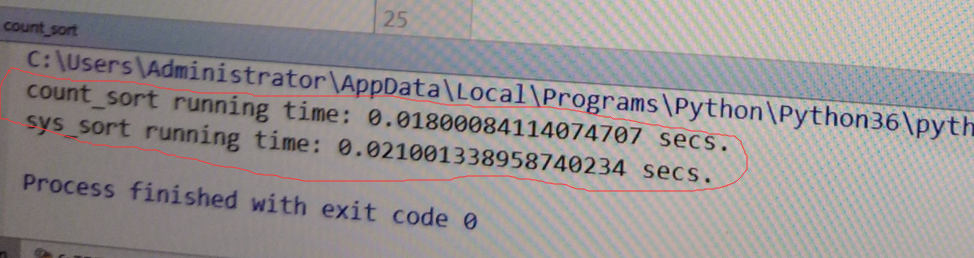
count_sort running time: 0.018001079559326172 secs.
Traceback (most recent call last):
File "E:/工作目录/python/test/count.py", line 35, in <module>
sys_sort(len(li1))
File "E:/工作目录/python/test/count.py", line 10, in wrapper
result = func(*args, **kwargs)
File "E:/工作目录/python/test/count.py", line 29, in sys_sort
li.sort()
AttributeError: 'int' object has no attribute 'sort'
Process finished with exit code 1
2、算法分析:
计数排序是一种以空间换时间的排序算法,并且只适用于待排序列中所有的数较为集中时,比如一组序列中的数据为0 1 2 3 4 999;就得开辟1000个辅助空间。
3、时间复杂度
- 时间复杂度:O(n)O(n)
- 空间复杂度:O(n)+O(N)O(n)+O(N)
- 是否稳定:是
- 优化措施:为了保障稳定性,算法中进行了多余的操作,如果不需要稳定性,可以优化时间。
4、应用场景
计数排序虽然时间复杂度较低,但需要满足的条件较多,如果能满足限制条件与空间需求,计数排序自然很快
1、计数排序的时间度理论为O(n+k),其中k为序列中数的范围。
2、不过当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)