一、引子
1、取指令(IF)和指令译码(ID)的阶段,是不需要停顿的
过去三讲,我主要为你介绍了结构冒险和数据冒险,以及增加资源、流水线停顿、操作数前推、乱序执行,这些解决各种“冒险”的技术方案。
在结构冒险和数据冒险中,你会发现,所有的流水线停顿操作都要从 指令执行阶段开始。流水线的前两个阶段,也就是取指令(IF)和指令译码(ID)的阶段,是不需要停顿的。CPU
会在流水线里面直接去取下一条指令,然后进行译码。
2、一旦遇到 if…else 这样的条件分支,或者 for/while 循环就会不成立
取指令和指令译码不会需要遇到任何停顿,这是基于一个假设。这个假设就是,所有的指令代码都是顺序加载执行的。不过这个假设,在执行的代码中,一旦遇到 if…else 这样的条件分支,
或者 for/while 循环,就会不成立。
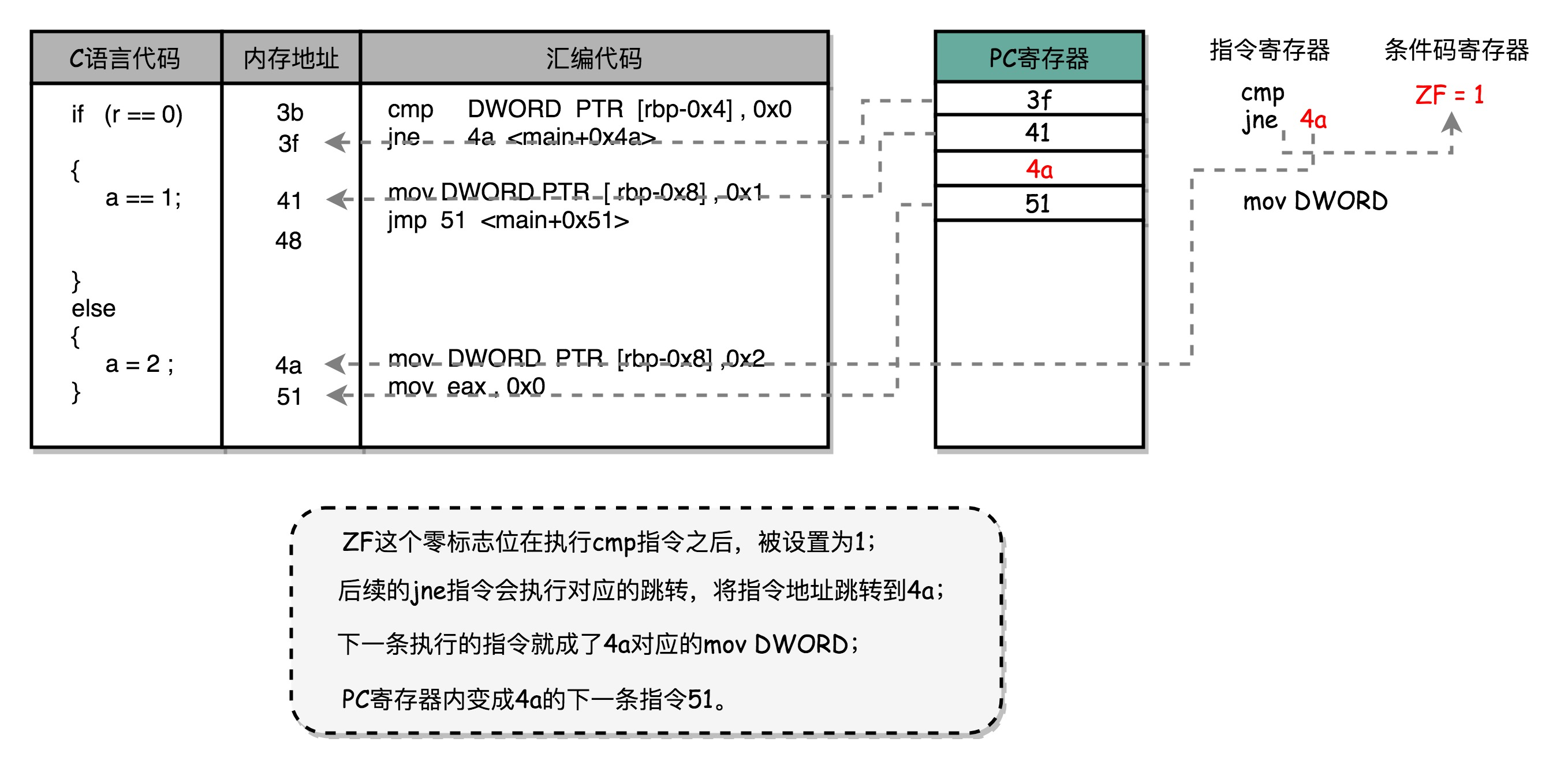
我们先来回顾一下,第6讲里讲的cmp比较指令、jmp和jle这样的条件跳转指令。可以看到,在jmp指令发生的时候,CPU可能会跳转去执行其他指令。jmp后的那一条指令是否应该顺序加载执行,
在流水线里面进行取指令的时候,我们没法知道。要等jmp指令执行完成,去更新了PC寄存器之后,我们才能知道,是否执行下一条指令,还是跳转到另外一个内存地址,去取别的指令
3、如何解决停顿
这种为了确保能取到正确的指令,而不得不进行等待延迟的情况,就是今天我们要讲的 控制冒险(ControlHarzard)。这也是流水线设计里最后一种冒险
二、分支预测:今天下雨了,明天还会继续下雨么?
在遇到了控制冒险之后,我们的CPU具体会怎么应对呢?除了流水线停顿,等待前面的jmp指令执行完成之后,再去取最新的指令,还有什么好办法吗?当然是有的。我们一起来看一看。
1、缩短分支延迟
1、缩短分支延迟
第一个办法,叫作 缩短分支延迟。回想一下我们的条件跳转指令,条件跳转指令其实进行了两种电路操作。
第一种,是进行条件比较。这个条件比较,需要的输入是,根据指令的opcode,就能确认的条件码寄存器。
第二种,是进行实际的跳转,也就是把要跳转的地址信息写入到PC寄存器。无论是opcode,还是对应的条件码寄存器,还是我们跳转的地址,都是在指令译码(ID)的阶段就能获得的。
而对应的条件码比较的电路,只要是简单的逻辑门电路就可以了,并不需要一个完整而复杂的ALU。
2、把一些计算结果更早地反馈到流水线中
所以,我们可以将条件判断、地址跳转,都提前到指令译码阶段进行,而不需要放在指令执行阶段。对应的,我们也要在CPU里面设计对应的旁路,在指令译码阶段,就提供对应的判断比较的电路。
这种方式,本质上和前面数据冒险的操作数前推的解决方案类似,就是在硬件电路层面,把一些计算结果更早地反馈到流水线中。这样反馈变得更快了,后面的指令需要等待的时间就变短了。
3、不过只是改造硬件,并不能彻底解决问题
不过只是改造硬件,并不能彻底解决问题。跳转指令的比较结果,仍然要在指令执行的时候才能知道。在流水线里,第一条指令进行指令译码的时钟周期里,我们其实就要去取下一条指令了。
这个时候,我们其实还没有开始指令执行阶段,自然也就不知道比较的结果。
2、分支预测
所以,这个时候,我们就引入了一个新的解决方案,叫作 分支预测(Branch Prediction)技术,也就是说,让我们的CPU来猜一猜,条件跳转后执行的指令,应该是哪一条。
最简单的分支预测技术,叫作“ 假装分支不发生”。顾名思义,自然就是仍然按照顺序,把指令往下执行。其实就是CPU预测,条件跳转一定不发生。这样的预测方法,
其实也是一种 静态预测技术。就好像猜硬币的时候,你一直猜正面,会有50%的正确率。
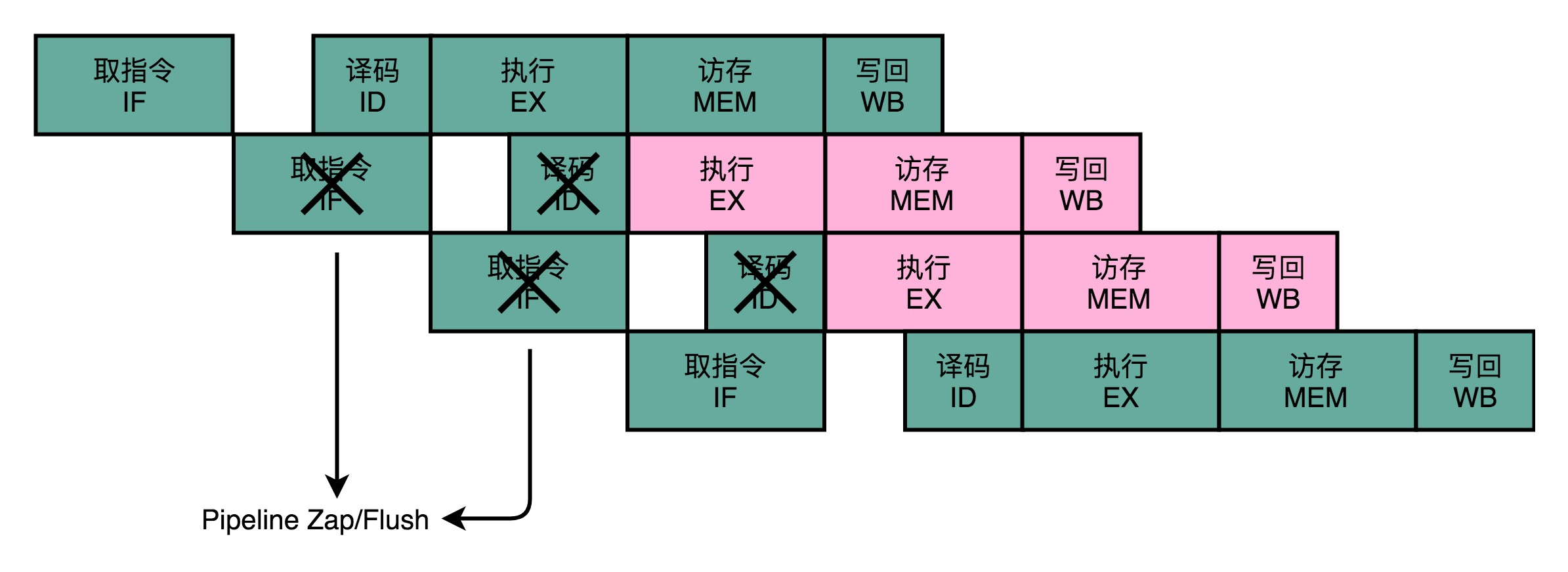
如果分支预测是正确的,我们自然赚到了。这个意味着,我们节省下来本来需要停顿下来等待的时间。如果分支预测失败了呢?那我们就把后面已经取出指令已经执行的部分,给丢弃掉。
这个丢弃的操作,在流水线里面,叫作Zap或者Flush。CPU不仅要执行后面的指令,对于这些已经在流水线里面执行到一半的指令,
我们还需要做对应的清除操作。比如,清空已经使用的寄存器里面的数据等等,这些清除操作,也有一定的开销。
所以,CPU需要提供对应的丢弃指令的功能,通过控制信号清除掉已经在流水线中执行的指令。只要对应的清除开销不要太大,我们就是划得来的。
3、动态分支预测
1、动态分支在天气预报中的应用
第三个办法,叫作 动态分支预测。上面的静态预测策略,看起来比较简单,预测的准确率也许有50%。但是如果运气不好,可能就会特别差。
于是,工程师们就开始思考,我们有没有更好的办法呢?比如,根据之前条件跳转的比较结果来预测,是不是会更准一点?
我们日常生活里,最经常会遇到的预测就是天气预报。如果没有气象台给你天气预报,你想要猜一猜明天是不是下雨,你会怎么办?
有一个简单的策略,就是完全根据今天的天气来猜。如果今天下雨,我们就预测明天下雨。如果今天天晴,就预测明天也不会下雨。这是一个很符合我们日常生活经验的预测。因为一般下雨天,
都是连着下几天,不断地间隔地发生“天晴-下雨-天晴-下雨”的情况并不多见。
那么,把这样的实践拿到生活中来是不是有效呢?我在这里给了一张2019年1月上海的天气情况的表格。
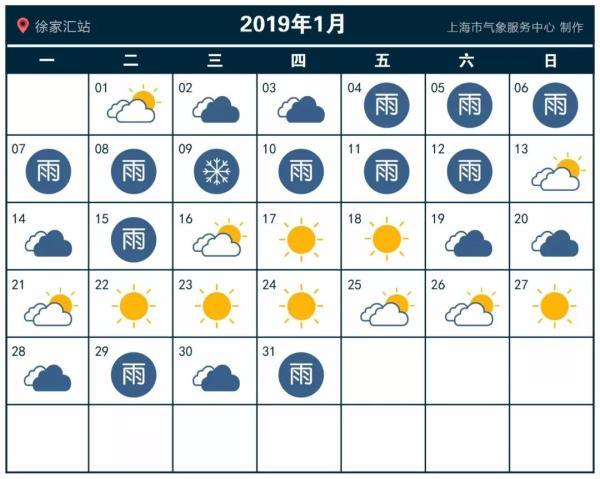
我们用前一天的是不是下雨,直接来预测后一天会不会下雨。这个表格里一共有31天,那我们就可以预测30次。你可以数一数,按照这种预测方式,我们可以预测正确23次,正确率是76.7%,
比随机预测的50%要好上不少。
2、同样的策略,可以放在分支预测上
而同样的策略,我们一样可以放在分支预测上。这种策略,我们叫 一级分支预测(One Level BranchPrediction),或者叫 1比特饱和计数(1-bit saturating counter)。这个方法,其实就是用一个比特,去记
录当前分支的比较情况,直接用当前分支的比较情况,来预测下一次分支时候的比较情况。
3、状态机
只用一天下雨,就预测第二天下雨,这个方法还是有些“草率”,我们可以用更多的信息,而不只是一次的分支信息来进行预测。于是,我们可以引入一个 状态机(State Machine)来做这个事情。
如果连续发生下雨的情况,我们就认为更有可能下雨。之后如果只有一天放晴了,我们仍然认为会下雨。在连续下雨之后,要连续两天放晴,我们才会认为之后会放晴。整个状态机的流转,可以参考我在文稿里放的图。

这个状态机里,我们一共有4个状态,所以我们需要2个比特来记录对应的状态。这样这整个策略,就可以叫作 2比特饱和计数,或者叫 双模态预测器(Bimodal Predictor)。
好了,现在你可以用这个策略,再去对照一下上面的天气情况。如果天气的初始状态我们放在“多半放晴”的状态下,我们预测的结果的正确率会是22次,也就是73.3%的正确率。可以看到,并不是更复杂的算
法,效果一定就更好。实际的预测效果,和实际执行的指令高度相关。
如果想对各种分支预测技术有所了解,Wikipedia里面有更详细的内容和更多的分支预测算法,你可以看看。
三、为什么循环嵌套的改变会影响性能?
同样循环了十亿次,第一段程序只花了5毫秒,而第二段程序则花了15毫秒,足足多了2倍。
说完了分支预测,现在我们先来看一个Java程序
public class BranchPrediction {
public static void main(String args[]) {
long start = System.currentTimeMillis();
for (int i = 0; i < 100; i++) {
for (int j = 0; j <1000; j ++) {
for (int k = 0; k < 10000; k++) {
}
}
}
long end = System.currentTimeMillis();
System.out.println("Time spent is " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < 10000; i++) {
for (int j = 0; j <1000; j ++) {
for (int k = 0; k < 100; k++) {
}
}
}
end = System.currentTimeMillis();
System.out.println("Time spent is " + (end - start) + "ms");
}
}
这是一个简单的三重循环,里面没有任何逻辑代码。我们用两种不同的循环顺序各跑一次。第一次,最外重循环循环了100次,第二重循环1000次,最内层的循环了10000次。第二次,
我们把顺序倒过来,最外重循环10000次,第二重还是1000次,最内层100次。
事实上,这段代码在这个专栏一开始的几讲里面,就有同学来提问,想要弄明白这里面的关窍。你可以先猜一猜,这样两次运行,花费的时间是一样的么?结果应该会让你大吃一惊。我们可以看看对应的命令行输出。
Time spent in first loop is 5ms Time spent in second loop is 15ms
同样循环了十亿次,第一段程序只花了5毫秒,而第二段程序则花了15毫秒,足足多了2倍。
这个差异就来自我们上面说的分支预测。我们在前面讲过,循环其实也是利用cmp和jle这样先比较后跳转的指令来实现的。如果对for循环的汇编代码或者机器代码的实现不太清楚,
你可以回头去复习一下第6讲。这里的代码,每一次循环都有一个cmp和jle指令。每一个 jle 就意味着,要比较条件码寄存器的状态,决定是顺序执行代码,
还是要跳转到另外一个地址。也就是说,在每一次循环发生的时候,都会有一次“分支”。
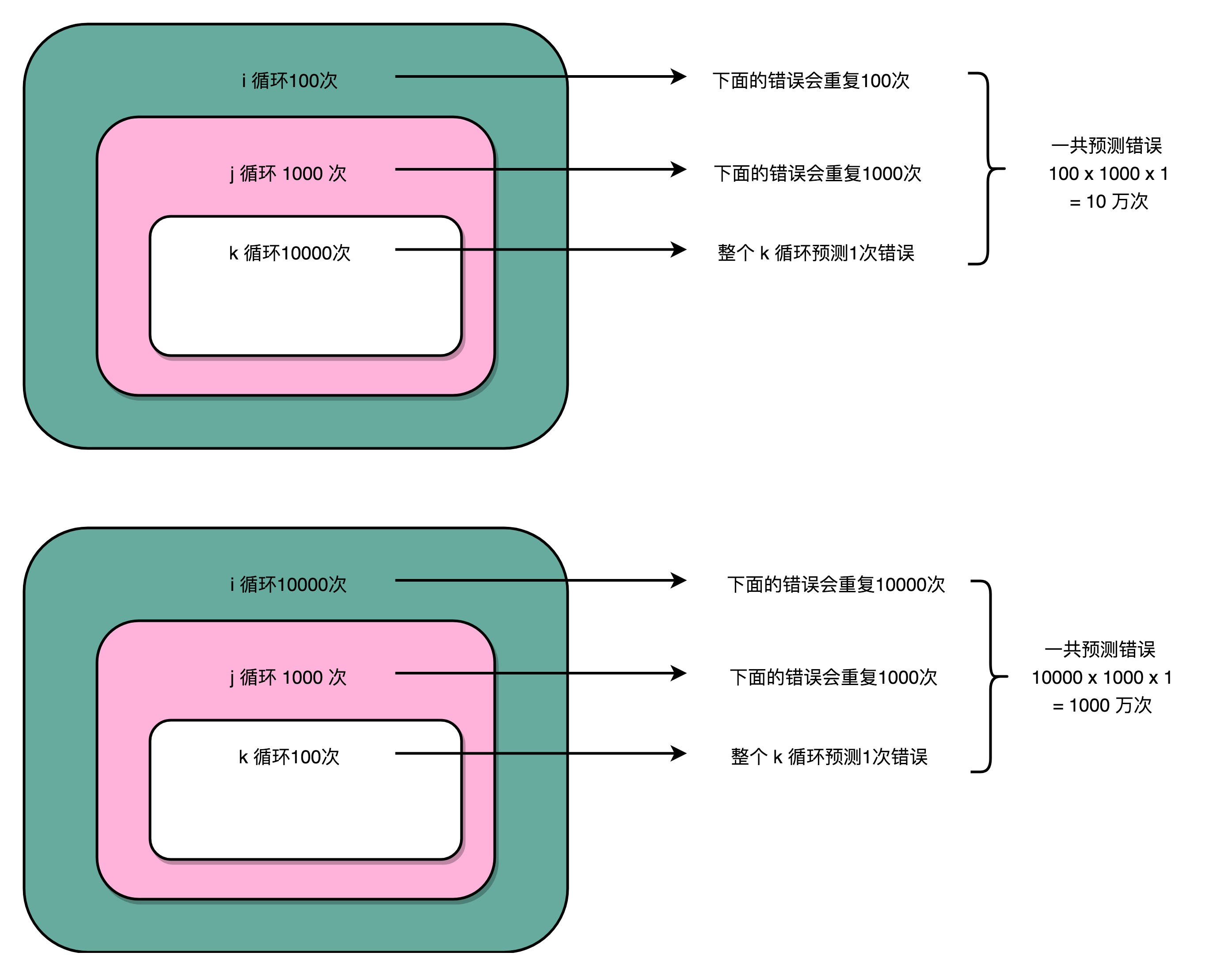
分支预测策略最简单的一个方式,自然是“ 假定分支不发生”。对应到上面的循环代码,就是循环始终会进行下去。在这样的情况下,上面的第一段循环,也就是内层 k 循环10000次的代码。每隔10000次,
才会发生一次预测上的错误。而这样的错误,在第二层 j 的循环发生的次数,是1000次。最外层的 i 的循环是100次。每个外层循环一次里面,都会发生1000次最内层 k 的循环的预测错误,所以一共会发生 100 × 1000 = 10万次预测错误。
上面的第二段循环,也就是内存k的循环100次的代码,则是每100次循环,就会发生一次预测错误。这样的错误,在第二层j的循环发生的次数,还是1000次。最外层 i 的循环是10000次,所以一共会发生 1000 ×10000 = 1000万次预测错误。
到这里,相信你能猜到为什么同样空转次数相同的循环代码,第一段代码运行的时间要少得多了。因为第一段代码发生“分支预测”错误的情况比较少,更多的计算机指令,
在流水线里顺序运行下去了,而不需要把运行到一半的指令丢弃掉,再去重新加载新的指令执行。
四、总结延伸
好了,这一讲,我给你讲解了什么是控制冒险,以及应对控制冒险的三个方式。
第一种方案,类似我们的操作数前推,其实是在改造我们的CPU功能,通过增加对应的电路的方式,来缩短分支带来的延迟。另外两种解决方案,无论是“假装分支不发生”,还是“动态分支预测”,
其实都是在进行“分支预测”。只是,“假装分支不发生”是一种简单的静态预测方案而已。
在动态分支预测技术里,我给你介绍了一级分支预测,或者叫1比特饱和计数的方法。其实就是认为,预测结果和上一次的条件跳转是一致的。在此基础上,我还介绍了利用更多信息的,就是2比特饱和计数,
或者叫双模态预测器的方法。这个方法其实也只是通过一个状态机,多看了一步过去的跳转比较结果。
这个方法虽然简单,但是却非常有效。在 SPEC 89 版本的测试当中,使用这样的饱和计数方法,预测的准确率能够高达93.5%。Intel的CPU,一直到Pentium时代,在还没有使用MMX指令集的时候,
用的就是这种分支预测方式。
这一讲的最后,我给你看了一个有意思的例子。通过交换内外循环的顺序,我们体验了一把控制冒险导致的性能差异。虽然执行的指令数是一样的,但是分支预测失败得多的程序,性能就要差上几倍。