你是不是感到很疑惑,浮点数的近似值究竟是怎么算出来的?浮点数的加法计算又是怎么回事儿?在实践应用中,我们怎么才用好浮点数呢?这一节,我们就一起来看这几个问题
一、浮点数的二进制转换
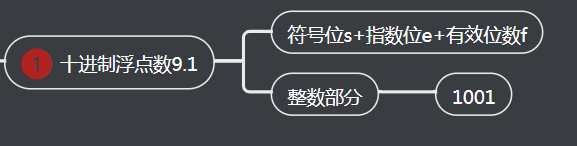
1、十进制浮点数9.1
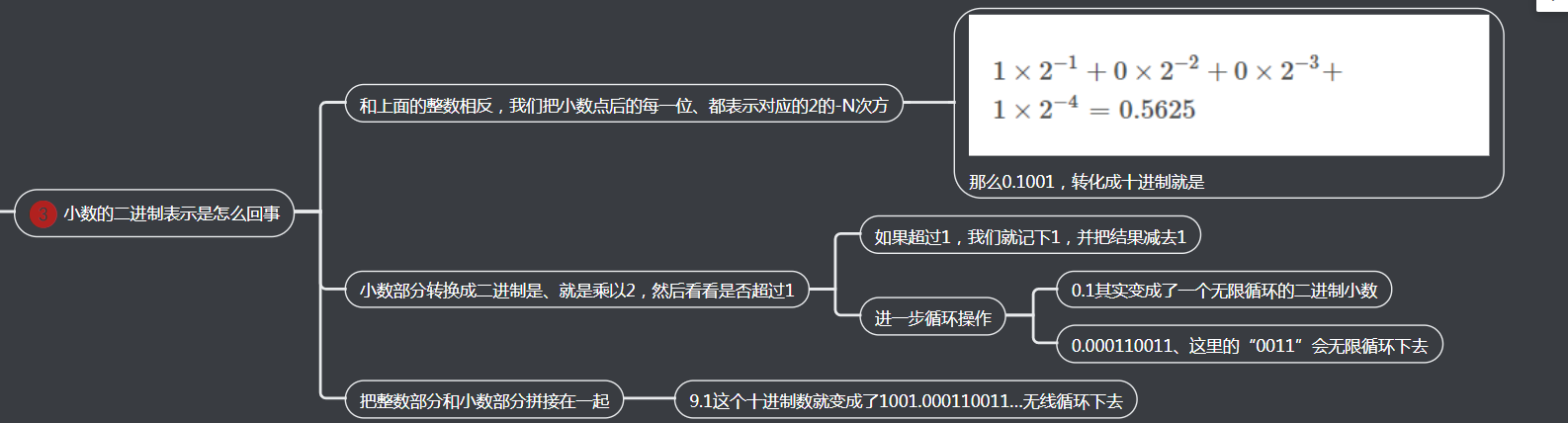
2、小数的二进制表示是怎么回事
3、浮点数其实是用二进制的科学计数法来表示的

4、为什么0.3+0.6=0.899999?

二、浮点数的加法和精度
1、浮点数的加法原理

2、比如0.5,表示成浮点数

实现这样一个加法,也只需要位移。和整数加法类似的半加器和全加器的方法就能够实现,在电路层面,也并没有引入太多新的复杂性。
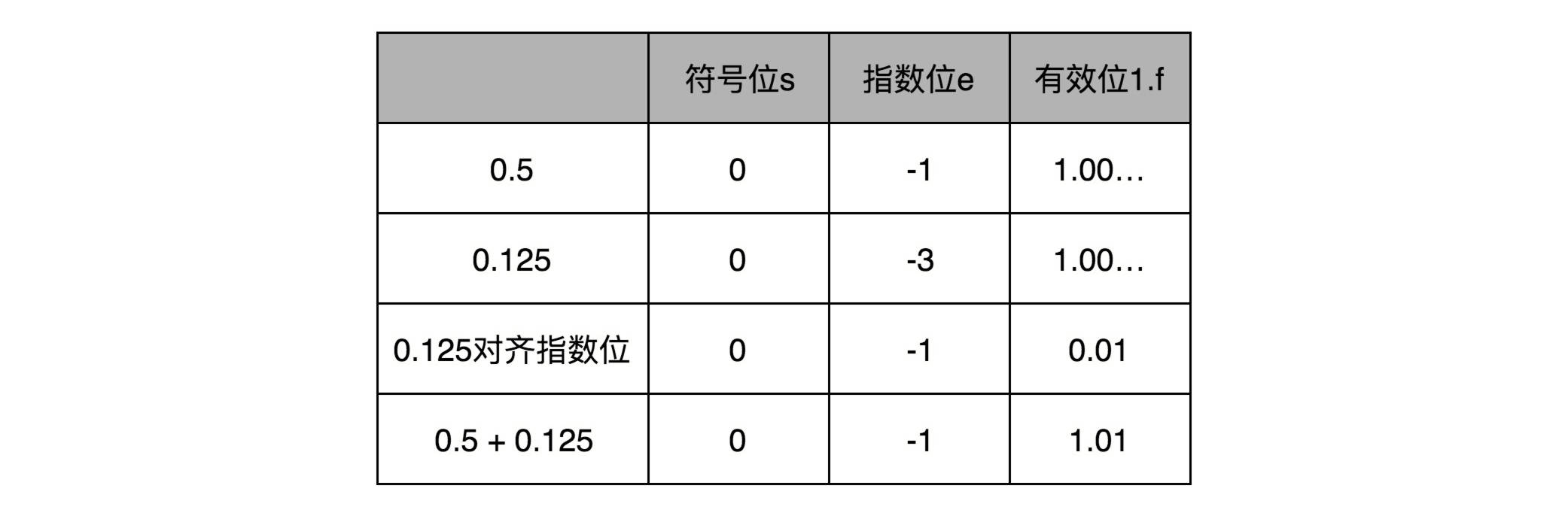
3、这个加法计算的浮点数的结果是不是正确
1、先对齐

2、在加法发生之前,就丢失精度

3、32位浮点数的加法

你可以试一下,我下面用一个简单的Java程序,让一个值为2000万的32位浮点数和1相加,你会发现,+1这个过程因为精度损失,被“完全抛弃”了。
public class FloatPrecision {
public static void main(String[] args) {
float a = 20000000.0f;
float b = 1.0f;
float c = a + b;
System.out.println("c is " + c);
float d = c - a;
System.out.println("d is " + d);
}
}
对应的输出结果就是:
c is 2.0E7 d is 0.0
三、Kahan Summation算法
那么,我们有没有什么办法来解决这个精度丢失问题呢?虽然我们在计算浮点数的时候,常常可以容忍一定的精度损失,但是像上面那样,
如果我们连续加2000万个1,2000万的数值都会被精度损失丢掉了,就会影响我们的计算结果。
在机器学习中的应用
我们可以做一个简单的实验,用一个循环相加2000万个1.0f,最终的结果会是1600万左右,而不是2000万。这是因为,
加到1600万之后的加法因为精度丢失都没有了。这个代码比起上面的使用2000万来加1.0更具有现实意义。
public class FloatPrecision {
public static void main(String[] args) {
float sum = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
sum += x;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果是:
sum is 1.6777216E7
面对这个问题,聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作Kahan Summation的算法来解决这个问题。
算法的对应代码我也放在文稿中了。从中你可以看到,同样是2000万个1.0f相加,用这种算法我们得到了准确的2000万的结果
public class KahanSummation {
public static void main(String[] args) {
float sum = 0.0f;
float c = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
float y = x - c;
float t = sum + y;
c = (t-sum)-y;
sum = t;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果是:
sum is 1.6777216E7
其实这个算法的原理其实并不复杂,就是在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算。
如果你对这个背后的数学原理特别感兴趣,可以去看一看Wikipedia链接里面对应的数学证明,也可以生成一些数据试一试这个算法。这个方法在实际的数值计算中也是常用的,也是大量数据累加
中,解决浮点数精度带来的“大数吃小数”问题的必备方案
四、总结延伸
1、浮点数的缺点

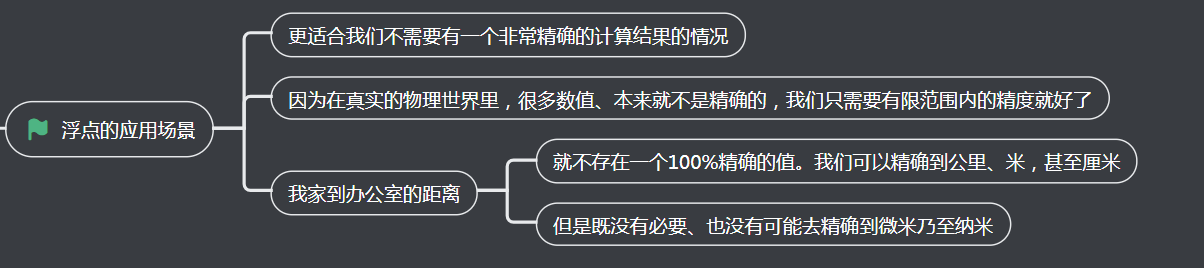
2、浮点数不适合的场景
3、浮点的应用场景