阮行止
上海洛谷网络科技有限公司 讲师
- intro
很有意思的问题。以往见过许多教材,对动态规划(DP)的引入属于“奉天承运,皇帝诏曰”式:不给出一点引入,见面即拿出一大堆公式吓人;学生则死啃书本,然后突然顿悟。针对入门者的教材不应该是这样的。恰好我给入门者讲过四次DP入门,迭代出了一套比较靠谱的教学方法,所以今天跑过来献丑。
现在,我们试着自己来一步步“重新发明”DP。
- 从一个生活问题谈起
先来看看生活中经常遇到的事吧——假设您是个土豪,身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w,需要用到尽量少的钞票。
依据生活经验,我们显然可以采取这样的策略:能用100的就尽量用100的,否则尽量用50的……依次类推。在这种策略下,666=6×100+1×50+1×10+1×5+1×1,共使用了10张钞票。
这种策略称为“贪心”:假设我们面对的局面是“需要凑出w”,贪心策略会尽快让w变得更小。能让w少100就尽量让它少100,这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明,贪心策略是正确的。
但是,如果我们换一组钞票的面值,贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11,那么我们在凑出15的时候,贪心策略会出错:
15=1×11+4×1 (贪心策略使用了5张钞票)
15=3×5 (正确的策略,只用3张钞票)
为什么会这样呢?贪心策略错在了哪里?
鼠目寸光。
刚刚已经说过,贪心策略的纲领是:“尽量使接下来面对的w更小”。这样,贪心策略在w=15的局面时,会优先使用11来把w降到4;但是在这个问题中,凑出4的代价是很高的,必须使用4×1。如果使用了5,w会降为10,虽然没有4那么小,但是凑出10只需要两张5元。
在这里我们发现,贪心是一种只考虑眼前情况的策略。
那么,现在我们怎样才能避免鼠目寸光呢?
如果直接暴力枚举凑出w的方案,明显复杂度过高。太多种方法可以凑出w了,枚举它们的时间是不可承受的。我们现在来尝试找一下性质。
重新分析刚刚的例子。w=15时,我们如果取11,接下来就面对w=4的情况;如果取5,则接下来面对w=10的情况。我们发现这些问题都有相同的形式:“给定w,凑出w所用的最少钞票是多少张?”接下来,我们用f(n)来表示“凑出n所需的最少钞票数量”。
那么,如果我们取了11,最后的代价(用掉的钞票总数)是多少呢?
明显 ext{cost} = f(4) + 1 = 4 + 1 = 5 ,它的意义是:利用11来凑出15,付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。
依次类推,马上可以知道:如果我们用5来凑出15,cost就是f(10) + 1 = 2 + 1 = 3 。
那么,现在w=15的时候,我们该取那种钞票呢?当然是各种方案中,cost值最低的那一个!
- 取11: ext{cost}=f(4)+1=4+1=5
- 取5: ext{cost}=f(10)+1=2+1=3
- 取1: ext{cost}=f(14)+1=4+1=5
显而易见,cost值最低的是取5的方案。我们通过上面三个式子,做出了正确的决策!
这给了我们一个至关重要的启示—— f(n) 只与 f(n-1),f(n-5),f(n-11) 相关;更确切地说:
f(n)=min{f(n-1),f(n-5),f(n-11)}+1
这个式子是非常激动人心的。我们要求出f(n),只需要求出几个更小的f值;既然如此,我们从小到大把所有的f(i)求出来不就好了?注意一下边界情况即可。代码如下:
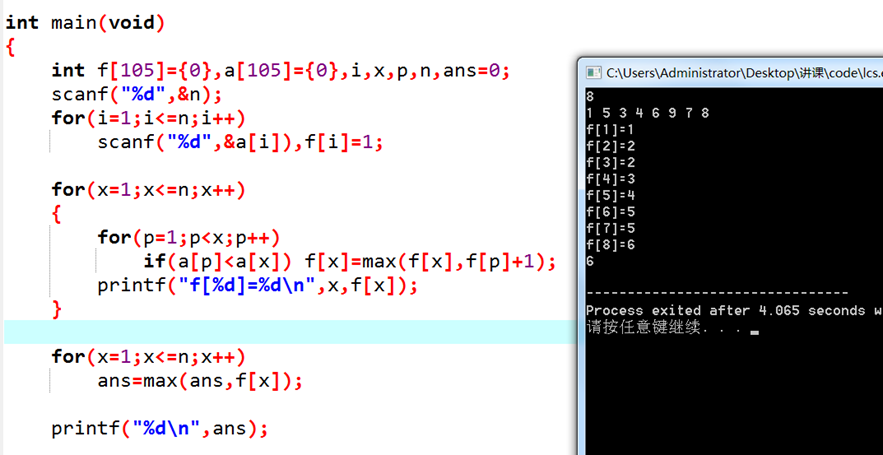
我们以 O(n) 的复杂度解决了这个问题。现在回过头来,我们看看它的原理:
- f(n) 只与f(n-1),f(n-5),f(n-11)的值相关。
- 我们只关心 f(w) 的值,不关心是怎么凑出w的。
这两个事实,保证了我们做法的正确性。它比起贪心策略,会分别算出取1、5、11的代价,从而做出一个正确决策,这样就避免掉了“鼠目寸光”!
它与暴力的区别在哪里?我们的暴力枚举了“使用的硬币”,然而这属于冗余信息。我们要的是答案,根本不关心这个答案是怎么凑出来的。譬如,要求出f(15),只需要知道f(14),f(10),f(4)的值。其他信息并不需要。我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n).
我们能这样干,取决于问题的性质:求出f(n),只需要知道几个更小的f©。我们将求解f©称作求解f(n)的“子问题”。
这就是DP(动态规划,dynamic programming).
将一个问题拆成几个子问题,分别求解这些子问题,即可推断出大问题的解。
思考题:请稍微修改代码,输出我们凑出w的方案。
2. 几个简单的概念
【无后效性】
一旦f(n)确定,“我们如何凑出f(n)”就再也用不着了。
要求出f(15),只需要知道f(14),f(10),f(4)的值,而f(14),f(10),f(4)是如何算出来的,对之后的问题没有影响。
“未来与过去无关”,这就是无后效性。
(严格定义:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。)
【最优子结构】
回顾我们对f(n)的定义:我们记“凑出n所需的最少钞票数量”为f(n).
f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解,我们即可算出w=15的最优解。
大问题的最优解可以由小问题的最优解推出,这个性质叫做“最优子结构性质”。
引入这两个概念之后,我们如何判断一个问题能否使用DP解决呢?
能将大问题拆成几个小问题,且满足无后效性、最优子结构性质。
- DP的典型应用:DAG最短路
问题很简单:给定一个城市的地图,所有的道路都是单行道,而且不会构成环。每条道路都有过路费,问您从S点到T点花费的最少费用。
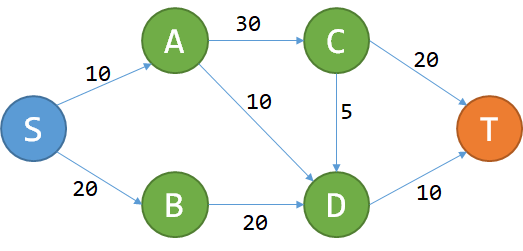
一张地图。边上的数字表示过路费。
这个问题能用DP解决吗?我们先试着记从S到P的最少费用为f§.
想要到T,要么经过C,要么经过D。从而f(T)=min{f©+20,f(D)+10}.
好像看起来可以DP。现在我们检验刚刚那两个性质:
- 无后效性:对于点P,一旦f§确定,以后就只关心f§的值,不关心怎么去的。
- 最优子结构:对于P,我们当然只关心到P的最小费用,即f§。如果我们从S走到T是 S o P o Q o T ,那肯定S走到Q的最优路径是 S o P o Q 。对一条最优的路径而言,从S走到沿途上所有的点(子问题)的最优路径,都是这条大路的一部分。这个问题的最优子结构性质是显然的。
既然这两个性质都满足,那么本题可以DP。式子明显为:
f§=min{f®+w_{R→P}}
其中R为有路通到P的所有的点, w_{R→P} 为R到P的过路费。
代码实现也很简单,拓扑排序即可。
- 对DP原理的一点讨论
【DP的核心思想】
DP为什么会快?
无论是DP还是暴力,我们的算法都是在可能解空间内,寻找最优解。
来看钞票问题。暴力做法是枚举所有的可能解,这是最大的可能解空间。
DP是枚举有希望成为答案的解。这个空间比暴力的小得多。
也就是说:DP自带剪枝。
DP舍弃了一大堆不可能成为最优解的答案。譬如:
15 = 5+5+5 被考虑了。
15 = 5+5+1+1+1+1+1 从来没有考虑过,因为这不可能成为最优解。
从而我们可以得到DP的核心思想:尽量缩小可能解空间。
在暴力算法中,可能解空间往往是指数级的大小;如果我们采用DP,那么有可能把解空间的大小降到多项式级。
一般来说,解空间越小,寻找解就越快。这样就完成了优化。
【DP的操作过程】
一言以蔽之:大事化小,小事化了。
将一个大问题转化成几个小问题;
求解小问题;
推出大问题的解。
【如何设计DP算法】
下面介绍比较通用的设计DP算法的步骤。
首先,把我们面对的局面表示为x。这一步称为设计状态。
对于状态x,记我们要求出的答案(e.g. 最小费用)为f(x).我们的目标是求出f(T).
找出f(x)与哪些局面有关(记为p),写出一个式子(称为状态转移方程),通过f§来推出f(x).
【DP三连】
设计DP算法,往往可以遵循DP三连:
我是谁? ——设计状态,表示局面
我从哪里来?
我要到哪里去? ——设计转移
设计状态是DP的基础。接下来的设计转移,有两种方式:一种是考虑我从哪里来(本文之前提到的两个例子,都是在考虑“我从哪里来”);另一种是考虑我到哪里去,这常见于求出f(x)之后,更新能从x走到的一些解。这种DP也是不少的,我们以后会遇到。
总而言之,“我从哪里来”和“我要到哪里去”只需要考虑清楚其中一个,就能设计出状态转移方程,从而写代码求解问题。前者又称pull型的转移,后者又称push型的转移。(这两个词是
@阮止雨
妹妹告诉我的,不知道源出处在哪)
思考题:如何把钞票问题的代码改写成“我到哪里去”的形式?
提示:求出f(x)之后,更新f(x+1),f(x+5),f(x+11).
5. 例题:最长上升子序列
扯了这么多形而上的内容,还是做一道例题吧。
最长上升子序列(LIS)问题:给定长度为n的序列a,从a中抽取出一个子序列,这个子序列需要单调递增。问最长的上升子序列(LIS)的长度。
e.g. 1,5,3,4,6,9,7,8的LIS为1,3,4,6,7,8,长度为6。
如何设计状态(我是谁)?
我们记 f(x) 为以 a_x 结尾的LIS长度,那么答案就是 max{f(x)} .
状态x从哪里推过来(我从哪里来)?
考虑比x小的每一个p:如果 a_x>a_p ,那么f(x)可以取f§+1.
解释:我们把 a_x 接在 a_p 的后面,肯定能构造一个以 a_x 结尾的上升子序列,长度比以 a_p 结尾的LIS大1.那么,我们可以写出状态转移方程了:
f(x)=max_{p<x , a_p<a_x }{f§}+1
至此解决问题。两层for循环,复杂度 O(n^2) .
从这三个例题中可以看出,DP是一种思想,一种“大事化小,小事化了”的思想。带着这种思想,DP将会成为我们解决问题的利器。
最后,我们一起念一遍DP三连吧——我是谁?我从哪里来?我要到哪里去?
- 习题
如果读者有兴趣,可以试着完成下面几个习题:
一、请采取一些优化手段,以 O(nlog n) 的复杂度解决LIS问题。
提示:可以参考这篇博客 Junior Dynamic Programming–动态规划初步·各种子序列问题
二、“按顺序递推”和“记忆化搜索”是实现DP的两种方式。请查阅资料,简单描述“记忆化搜索”是什么。并采用记忆化搜索写出钞票问题的代码,然后完成P1541 乌龟棋 - 洛谷 。
三、01背包问题是一种常见的DP模型。请完成P1048 采药 - 洛谷。
徐凯强 Andy
永远好奇
3,104 人赞同了该回答
动态规划中递推式的求解方法不是动态规划的本质。
我曾经作为省队成员参加过NOI,保送之后也给学校参加NOIP的同学多次讲过动态规划,我试着讲一下我理解的动态规划,争取深入浅出。希望你看了我的答案,能够喜欢上动态规划。
-
动态规划的本质,是对问题状态的定义和状态转移方程的定义。
引自维基百科
dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.
动态规划是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决。
本题下的其他答案,大多都是在说递推的求解方法,但如何拆分问题,才是动态规划的核心。
而拆分问题,靠的就是状态的定义和状态转移方程的定义。 -
什么是状态的定义?
首先想说大家千万不要被下面的数学式吓到,这里只涉及到了函数相关的知识。
我们先来看一个动态规划的教学必备题:
给定一个数列,长度为N,
求这个数列的最长上升(递增)子数列(LIS)的长度.
以
1 7 2 8 3 4
为例。
这个数列的最长递增子数列是 1 2 3 4,长度为4;
次长的长度为3, 包括 1 7 8; 1 2 3 等.
要解决这个问题,我们首先要定义这个问题和这个问题的子问题。
有人可能会问了,题目都已经在这了,我们还需定义这个问题吗?需要,原因就是这个问题在字面上看,找不出子问题,而没有子问题,这个题目就没办法解决。
所以我们来重新定义这个问题:
给定一个数列,长度为N,
设F_{k}为:以数列中第k项结尾的最长递增子序列的长度.
求F_{1}…F_{N} 中的最大值.
显然,这个新问题与原问题等价。
而对于F_{k}来讲,F_{1} … F_{k-1}都是F_{k}的子问题:因为以第k项结尾的最长递增子序列(下称LIS),包含着以第1…k-1中某项结尾的LIS。
上述的新问题F_{k}也可以叫做状态,定义中的“F_{k}为数列中第k项结尾的LIS的长度”,就叫做对状态的定义。
之所以把F_{k}做“状态”而不是“问题” ,一是因为避免跟原问题中“问题”混淆,二是因为这个新问题是数学化定义的。
对状态的定义只有一种吗?当然不是。
我们甚至可以二维的,以完全不同的视角定义这个问题:
给定一个数列,长度为N,
设F_{i, k}为:
在前i项中的,长度为k的最长递增子序列中,最后一位的最小值. 1leq kleq N.
若在前i项中,不存在长度为k的最长递增子序列,则F_{i, k}为正无穷.
求最大的x,使得F_{N,x}不为正无穷。
这个新定义与原问题的等价性也不难证明,请读者体会一下。
上述的F_{i, k}就是状态,定义中的“F_{i, k}为:在前i项中,长度为k的最长递增子序列中,最后一位的最小值”就是对状态的定义。
- 什么是状态转移方程?
上述状态定义好之后,状态和状态之间的关系式,就叫做状态转移方程。
比如,对于LIS问题,我们的第一种定义:
设F_{k}为:以数列中第k项结尾的最长递增子序列的长度.
设A为题中数列,状态转移方程为:
F_{1} = 1 (根据状态定义导出边界情况)
F_{k}=max(F_{i}+1 | A_{k}>A_{i}, iin (1…k-1)) (k>1)
用文字解释一下是:
以第k项结尾的LIS的长度是:保证第i项比第k项小的情况下,以第i项结尾的LIS长度加一的最大值,取遍i的所有值(i小于k)。
第二种定义:
设F_{i, k}为:在数列前i项中,长度为k的递增子序列中,最后一位的最小值
设A为题中数列,状态转移方程为:
若A_{i}>F_{i-1,k-1}则F_{i,k}=min(A_{i},F_{i-1,k})
否则:F_{i,k}=F_{i-1,k}
(边界情况需要分类讨论较多,在此不列出,需要根据状态定义导出边界情况。)
大家套着定义读一下公式就可以了,应该不难理解,就是有点绕。
这里可以看出,这里的状态转移方程,就是定义了问题和子问题之间的关系。
可以看出,状态转移方程就是带有条件的递推式。
- 动态规划迷思
本题下其他用户的回答跟动态规划都有或多或少的联系,我也讲一下与本答案的联系。
a. “缓存”,“重叠子问题”,“记忆化”:
这三个名词,都是在阐述递推式求解的技巧。以Fibonacci数列为例,计算第100项的时候,需要计算第99项和98项;在计算第101项的时候,需要第100项和第99项,这时候你还需要重新计算第99项吗?不需要,你只需要在第一次计算的时候把它记下来就可以了。
上述的需要再次计算的“第99项”,就叫“重叠子问题”。如果没有计算过,就按照递推式计算,如果计算过,直接使用,就像“缓存”一样,这种方法,叫做“记忆化”,这是递推式求解的技巧。这种技巧,通俗的说叫“花费空间来节省时间”。都不是动态规划的本质,不是动态规划的核心。
b. “递归”:
递归是递推式求解的方法,连技巧都算不上。
c. “无后效性”,“最优子结构”:
上述的状态转移方程中,等式右边不会用到下标大于左边i或者k的值,这是"无后效性"的通俗上的数学定义,符合这种定义的状态定义,我们可以说它具有“最优子结构”的性质,在动态规划中我们要做的,就是找到这种“最优子结构”。
在对状态和状态转移方程的定义过程中,满足“最优子结构”是一个隐含的条件(否则根本定义不出来)。对状态和“最优子结构”的关系的进一步解释,什么是动态规划?动态规划的意义是什么? - 王勐的回答 写的很好,大家可以去读一下。
需要注意的是,一个问题可能有多种不同的状态定义和状态转移方程定义,存在一个有后效性的定义,不代表该问题不适用动态规划。这也是其他几个答案中出现的逻辑误区:
动态规划方法要寻找符合“最优子结构“的状态和状态转移方程的定义,在找到之后,这个问题就可以以“记忆化地求解递推式”的方法来解决。而寻找到的定义,才是动态规划的本质。
有位答主说:
分治在求解每个子问题的时候,都要进行一遍计算
动态规划则存储了子问题的结果,查表时间为常数
这就像说多加辣椒的菜就叫川菜,多加酱油的菜就叫鲁菜一样,是存在误解的。
文艺的说,动态规划是寻找一种对问题的观察角度,让问题能够以递推(或者说分治)的方式去解决。寻找看问题的角度,才是动态规划中最耀眼的宝石!(大雾)
王勐
3,648 人赞同了该回答
动态规划的本质不在于是递推或是递归,也不需要纠结是不是内存换时间。
理解动态规划并不需要数学公式介入,只是完全解释清楚需要点篇幅…首先需要明白哪些问题不是动态规划可以解决的,才能明白为神马需要动态规划。不过好处时顺便也就搞明白了递推贪心搜索和动规之间有什么关系,以及帮助那些总是把动规当成搜索解的同学建立动规的思路。当然熟悉了之后可以直接根据问题的描述得到思路,如果有需要的话再补充吧。
动态规划是对于 某一类问题 的解决方法!!重点在于如何鉴定“某一类问题”是动态规划可解的而不是纠结解决方法是递归还是递推!
怎么鉴定dp可解的一类问题需要从计算机是怎么工作的说起…计算机的本质是一个状态机,内存里存储的所有数据构成了当前的状态,CPU只能利用当前的状态计算出下一个状态(不要纠结硬盘之类的外部存储,就算考虑他们也只是扩大了状态的存储容量而已,并不能改变下一个状态只能从当前状态计算出来这一条铁律)
当你企图使用计算机解决一个问题是,其实就是在思考如何将这个问题表达成状态(用哪些变量存储哪些数据)以及如何在状态中转移(怎样根据一些变量计算出另一些变量)。所以所谓的空间复杂度就是为了支持你的计算所必需存储的状态最多有多少,所谓时间复杂度就是从初始状态到达最终状态中间需要多少步!
太抽象了还是举个例子吧:
比如说我想计算第100个非波那契数,每一个非波那契数就是这个问题的一个状态,每求一个新数字只需要之前的两个状态。所以同一个时刻,最多只需要保存两个状态,空间复杂度就是常数;每计算一个新状态所需要的时间也是常数且状态是线性递增的,所以时间复杂度也是线性的。
上面这种状态计算很直接,只需要依照固定的模式从旧状态计算出新状态就行(a[i]=a[i-1]+a[i-2]),不需要考虑是不是需要更多的状态,也不需要选择哪些旧状态来计算新状态。对于这样的解法,我们叫递推。
非波那契那个例子过于简单,以至于让人忽视了阶段的概念,所谓阶段是指随着问题的解决,在同一个时刻可能会得到的不同状态的集合。非波那契数列中,每一步会计算得到一个新数字,所以每个阶段只有一个状态。想象另外一个问题情景,假如把你放在一个围棋棋盘上的某一点,你每一步只能走一格,因为你可以东南西北随便走,所以你当你同样走四步可能会处于很多个不同的位置。从头开始走了几步就是第几个阶段,走了n步可能处于的位置称为一个状态,走了这n步所有可能到达的位置的集合就是这个阶段下所有可能的状态。
现在问题来了,有了阶段之后,计算新状态可能会遇到各种奇葩的情况,针对不同的情况,就需要不同的算法,下面就分情况来说明一下:
假如问题有n个阶段,每个阶段都有多个状态,不同阶段的状态数不必相同,一个阶段的一个状态可以得到下个阶段的所有状态中的几个。那我们要计算出最终阶段的状态数自然要经历之前每个阶段的某些状态。
好消息是,有时候我们并不需要真的计算所有状态,比如这样一个弱智的棋盘问题:从棋盘的左上角到达右下角最短需要几步。答案很显然,用这样一个弱智的问题是为了帮助我们理解阶段和状态。某个阶段确实可以有多个状态,正如这个问题中走n步可以走到很多位置一样。但是同样n步中,有哪些位置可以让我们在第n+1步中走的最远呢?没错,正是第n步中走的最远的位置。换成一句熟悉话叫做“下一步最优是从当前最优得到的”。所以为了计算最终的最优值,只需要存储每一步的最优值即可,解决符合这种性质的问题的算法就叫贪心。如果只看最优状态之间的计算过程是不是和非波那契数列的计算很像?所以计算的方法是递推。
既然问题都是可以划分成阶段和状态的。这样一来我们一下子解决了一大类问题:一个阶段的最优可以由前一个阶段的最优得到。
如果一个阶段的最优无法用前一个阶段的最优得到呢?
什么你说只需要之前两个阶段就可以得到当前最优?那跟只用之前一个阶段并没有本质区别。最麻烦的情况在于你需要之前所有的情况才行。
再来一个迷宫的例子。在计算从起点到终点的最短路线时,你不能只保存当前阶段的状态,因为题目要求你最短,所以你必须知道之前走过的所有位置。因为即便你当前再的位置不变,之前的路线不同会影响你的之后走的路线。这时你需要保存的是之前每个阶段所经历的那个状态,根据这些信息才能计算出下一个状态!
每个阶段的状态或许不多,但是每个状态都可以转移到下一阶段的多个状态,所以解的复杂度就是指数的,因此时间复杂度也是指数的。哦哦,刚刚提到的之前的路线会影响到下一步的选择,这个令人不开心的情况就叫做有后效性。
刚刚的情况实在太普遍,解决方法实在太暴力,有没有哪些情况可以避免如此的暴力呢?
契机就在于后效性。
有一类问题,看似需要之前所有的状态,其实不用。不妨也是拿最长上升子序列的例子来说明为什么他不必需要暴力搜索,进而引出动态规划的思路。
假装我们年幼无知想用搜索去寻找最长上升子序列。怎么搜索呢?需要从头到尾依次枚举是否选择当前的数字,每选定一个数字就要去看看是不是满足“上升”的性质,这里第i个阶段就是去思考是否要选择第i个数,第i个阶段有两个状态,分别是选和不选。哈哈,依稀出现了刚刚迷宫找路的影子!咦慢着,每次当我决定要选择当前数字的时候,只需要和之前选定的一个数字比较就行了!这是和之前迷宫问题的本质不同!这就可以纵容我们不需要记录之前所有的状态啊!既然我们的选择已经不受之前状态的组合的影响了,那时间复杂度自然也不是指数的了啊!虽然我们不在乎某序列之前都是什么元素,但我们还是需要这个序列的长度的。所以我们只需要记录以某个元素结尾的LIS长度就好!因此第i个阶段的最优解只是由前i-1个阶段的最优解得到的,然后就得到了DP方程(感谢
@韩曦
指正)
LIS(i)=max{LIS(j)+1}
j<i and a[j] < a[i]
所以一个问题是该用递推、贪心、搜索还是动态规划,完全是由这个问题本身阶段间状态的转移方式决定的!
每个阶段只有一个状态->递推;
每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心;
每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索;
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到
这个性质叫做最优子结构;
而不管之前这个状态是如何得到的
这个性质叫做无后效性。
另:其实动态规划中的最优状态的说法容易产生误导,以为只需要计算最优状态就好,LIS问题确实如此,转移时只用到了每个阶段“选”的状态。但实际上有的问题往往需要对每个阶段的所有状态都算出一个最优值,然后根据这些最优值再来找最优状态。比如背包问题就需要对前i个包(阶段)容量为j时(状态)计算出最大价值。然后在最后一个阶段中的所有状态种找到最优值。
Tim Shen
Twitter: @timshen_
142 人赞同了该回答
// 发现上面已经有人提到了最短路了。。但是动态规划真的不喜欢有环的图啊QAQ
动态规划不是个具体的算法,是一个框架。框架是死的,但框架里填什么全看人。
这个框架就是有向无环图。图中每个点都存着一个值。你去把图论刷一遍,弄弄拓扑排序之后,就会明白,动态规划就是对图中所有点执行拓扑排序,再依照拓扑序让每个点更新自己指向的节点的值的过程。
至于图中点怎么定义,边怎么定义,值怎么定义,“更新”怎么定义,那就是考验建图论模型的能力了,我也没能力讲出个系统规律来。
这时候动态规划那些概念都能一一对应了。所谓最优子结构就是我可以证明只要按着拓扑序来更新,保证能得到最优解。无后效性呢,就是图不能有环。至于记忆化嘛,就是在每个点上存一个值了。递推嘛就是把拓扑序正着来一遍,递归嘛就是把拓扑序反着来一遍。都没什么新鲜东西的。
值得一提的是,根据上述的定义,动态规划不如最短路径强劲(觉得不好理解的请看后面的更新)。因为最短路径可以反复迭代,而动态规划必须一遍扫完。
也就是说,不要管什么动态规划了,只要是动态规划,最短路径都能解:)动态规划点里的值嘛就是最短距离了,一个点对另一个点的更新嘛就是最短路径的更新了。
若是连最短路径也不能活学活使,那还是背背书让老师开心就行了。
------------------ 更新 ------------------
对于有向无环图,按照拓扑序更新后继节点就是求最短路。通用的最短路算法在此依然适用。另外,通用的最短路算法仍然能解部分带环的图,所以在此可以把拓扑排序规约到最短路。当然有效率上的差别,但是我提这整个一大段只是希望用此模型辅助理解,降低学习曲线斜率而已,所以从“新的知识点越少越好”的角度,规约到最短路是最省力的了。
真写还是要注意效率的,能用循环就循环,能递归+记忆化就行。别傻乎乎地建图就行了。至于真正如何用代码实现,循环用什么姿势展开能达成拓扑序,有向无环图有没有分层关系从而能导致用滚动数组优化空间,都是一些后面要掌握的技巧了,但是应该机械得很。
拿“背包九讲”来说吧,可以尝试给0/1背包和无限背包问题画图,就明白为什么二者命令式语言实现中的循环是那么的似是而非。其实他俩状态图完全不一样,而且0/1背包的状态更复杂。但是通过对0/1背包进行滚动数组(严格来讲比滚动数组还变态,因为已经不是两个数组来回滚了,是同一个数组后面覆盖前面的)的优化,可以把存状态的数组减少到一维,结果代码就长得和完全背包只差一点点了。
具体点说,0/1背包的状态是二元组(i, j)表示花费为i时,前j个元素。状态中存值为最大能得到的利益。每个状态出两条边,即第j+1个物品选还是不选。这个图画出来是个二维的节点阵列,有明显的层次关系(j到j+1)。
而完全背包更简单,状态就是当前花费,每个状态的出边数和物品数相当。
顺带扯一句,这也是正则表达式中"a*"比"a{5, 81}“要好实现的原因。
至于树状动态规划,那就更贴近有向无环图的解法了,对树的后序遍历和拓扑排序如出一辙。
作者:Coldwings
首先明确:动态规划是用来求解最优化问题的一种方法。常规算法书上强调的是无后效性和最优子结构描述,这套理论是正确的,但是适用与否与你的状态表述有关。至于划分阶段什么的就有些扯淡了:动态规划不一定有所谓的阶段。其实质是状态空间的状态转移。下面的理解为我个人十年竞赛之总结。基本上在oi和acm中我没有因为动态规划而失手过。所有的决策类求最优解的问题都是在状态空间内找一个可以到达的最佳状态。搜索的方式是去遍历每一个点,而动态规划则是把状态空间变形,由此变成从初始到目标状态的最短路问题。依照这种描述:假若你的问题的结论包含若干决策,则可以认为从初始状态(边界条件)到解中间的决策流程是一个决策状态空间中的转移路线。前提是:你的状态描述可以完整且唯一地覆盖所有有效的状态空间中的点,且转移路线包含所有可能的路径。这个描述是包含动态规划两大条件的。所谓无后效性,指状态间的转移与如何到达某状态无关。如果有关,意味着你的状态描述不能完整而唯一地包括每一个状态。如果你发现一个状态转移有后效性,很简单,把会引起后效性的参数作为状态描述的一部分放进去将其区分开来就可以了;最优子结构说明转移路线包含了所有可能的路径,如果不具备最优子结构,意味着有部分情况没有在转移中充分体现,增加转移的描述就可以了。最终所有的搜索问题都可以描述成状态空间内的状态转移方程,只是有可能状态数量是指数阶的,有可能不满足计算要求罢了。这样的描述下,所有的动态规划问题都可以转变为状态空间内大量可行状态点和有效转移构成的图的从初始状态到最终状态的最短路问题。于是乎,对于动态规划,他的本质就是图论中的最短路;阶段可以去除,因为不一定有明确的阶段划分。